Autoencodeurs variationnels#
Les autoencodeurs variationnels sont, comme les GAN (abordés dans le cours suivant), des modèles génératifs, c’est-à-dire des modèles probabilistes \(p\) pouvant être utilisés pour simuler (ou générer) des données réalistes \(\boldsymbol x\sim p(\boldsymbol x,\boldsymbol\theta)\), aussi proches que possible de la vraie (mais inconnue) distribution des données \(p(\boldsymbol x)\), pour laquelle seul un échantillon de données est disponible.
Le paysage de ces modèles génératifs s’est beaucoup peuplé depuis 2014 (Fig. 62).

Fig. 62 Paysage des modèles génératifs (Source: Song et al., CVPR 2023)#
Dans ce cours, nous aborderons uniquement les autoencodeurs variationnels (VAE), les réseaux antagonistes générateurs (GAN) et ferons une brève introduction aux modèles de diffusion (DDPM, pour Denoising Diffusion Probabilistic Models)
Inférence variationnelle#
Modèles à variables latentes#
Un modèle à variables latentes met en relation un ensemble de variables observables \(\boldsymbol x\in \mathcal X\) avec un ensemble de variables latentes \(\boldsymbol h\in \mathcal H\)
Si \(\boldsymbol h\) sont des facteurs causaux pour \(\boldsymbol x\), alors échantillonner selon \(p(\boldsymbol x|\boldsymbol h)\) permet de créer un modèle génératif de \(\mathcal H\) vers \(\mathcal X\).
Pour l’inférence, étant donnée \(p(\boldsymbol x,\boldsymbol h)\), il « suffit » de calculer
Malheureusement, \(p(\boldsymbol x)\) est inaccessible.
Inférence variationnelle#
L’inférence variationnelle transforme l’estimation de \(p(\boldsymbol h|\boldsymbol x)\) en un problème d’optimisation.
On considère une famille de distributions \(q_{\boldsymbol\phi} (\boldsymbol{h}|\boldsymbol x)\) approchant \(p(\boldsymbol{h}|\boldsymbol x)\), où \(\boldsymbol \phi\) sont les paramètres variationnels. Ces paramètres sont optimisés pour minimiser une distance entre \(q_{\boldsymbol\phi} (\boldsymbol{h}|\boldsymbol x)\) et \(p(\boldsymbol x,\boldsymbol h)\). Parmi toutes les distances possibles, on retient la divergence de Kullback-Leibler
et ainsi :
Le dernier terme \(log(p(\boldsymbol x)\) reste cependant toujours inaccessible.
Cependant,
avec ELBO(Evidence Lower Bound Objective) définie par
Dans l’équation prédécente, on a éliminé \(log(p(\boldsymbol x))\) qui ne dépend pas de \(\boldsymbol\phi\).
En maximisant la fonction \(ELBO(\boldsymbol x,\boldsymbol\phi)\) :
le premier terme encourage les distributions à converger dans les configurations des variables latentes \(\boldsymbol h\) expliquant les données observées
le second terme force les distribution à être proches du prior.
Finalement, étant donné un échantillon \(E_a = \{\boldsymbol x_i,i\in[\![1,N]\!]\}\), la fonction objectif finale est
Pour la maximiser, on peut utiliser une montée de gradient, maix \(\nabla_{\boldsymbol\phi}ELBO(\boldsymbol x_i,\boldsymbol \phi)\) est en général difficile à calculer.
Autoencodeurs variationnels#
Principe#
Un autoencodeur variationnel (VAE) est un modèle profond à variables latentes (Fig. 63) tel que :
\(p(\boldsymbol h)\) est prescrit à l’avance
la vraisemblance \(p_{\boldsymbol\theta}(\boldsymbol x|\boldsymbol h)\) est un décodeur (réseau génératif) \(D_{\boldsymbol\theta}\) tel que \(\boldsymbol\Phi = D_{\boldsymbol\theta}(\boldsymbol h)\) où \(\boldsymbol \Phi\) sont les paramètres de la distribution des données. Par exemple
la distribution approchée \(q_{\boldsymbol\phi}(\boldsymbol h|\boldsymbol x)\) est paramétrée par un encodeur (réseau d’inférence) \(E_{\boldsymbol\phi}\) tel que \(\boldsymbol\nu = E_{\boldsymbol\phi}(\boldsymbol x)\) sont les paramètres de la distribution approchée. Par exemple :
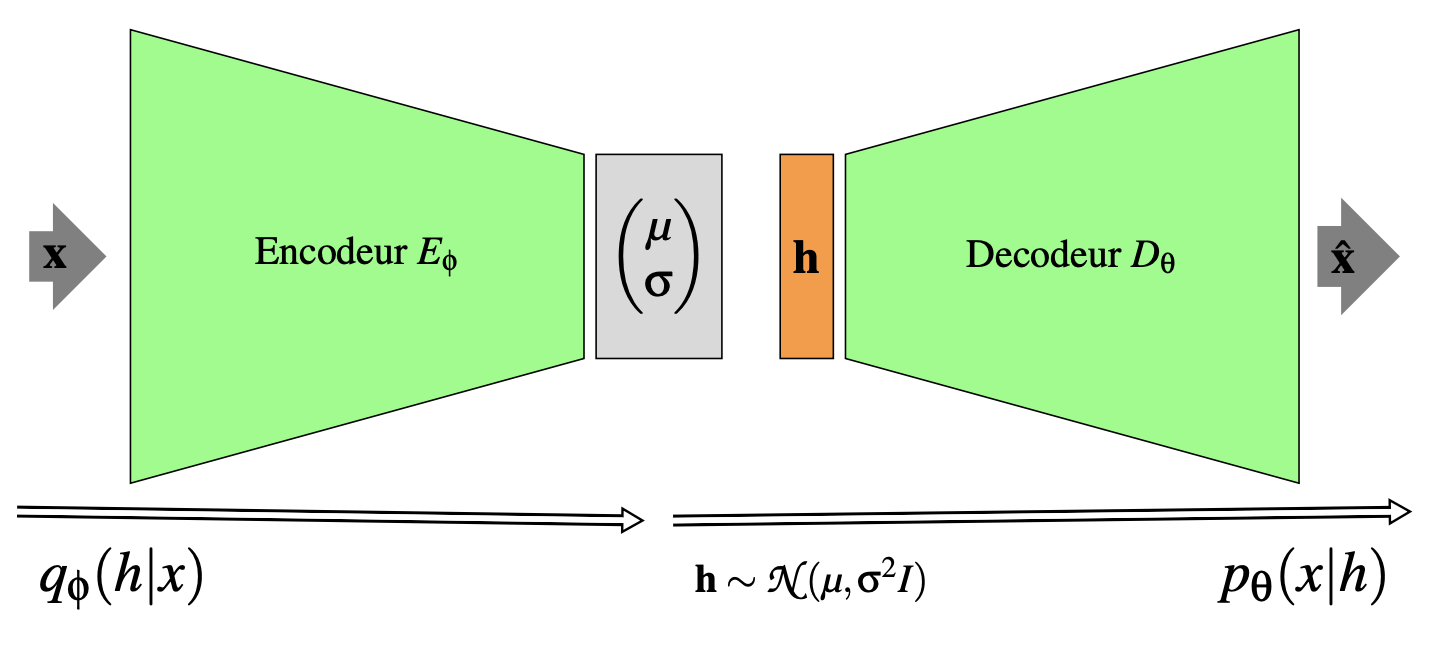
Fig. 63 Architecture générale d’un autoencodeur variationnel#
Comme précédemment, on peut utiliser l’inférence variationnelle pour optimiser de manière jointe \(\boldsymbol\theta\) et \(\boldsymbol\phi\) :
Etant donné \(D_{\boldsymbol\theta}\), on veut ajuster les variables latentes, en optimissant \(\boldsymbol\phi\), de sorte à ce qu’elles expliquent les données observées, tout en restant près de données générées par \(p(\boldsymbol h)\). De même, étant donné \(E_{\boldsymbol\phi}\), on veut ajuster les variables observées, en optimissant \(\boldsymbol\theta\), de telle sorte qu’elles soient le plus possible expliquées par les variables latentes.
L’optimisation peut se faire par montée de gradients :
\(\nabla_{\boldsymbol\theta}ELBO(\boldsymbol x,\boldsymbol\theta,\boldsymbol\phi) = \mathbb{E}_{q_{\boldsymbol\phi}(\boldsymbol h|\boldsymbol x)}\left [\nabla_{\boldsymbol\theta}(log p_{\boldsymbol\theta}(\boldsymbol x|\boldsymbol h))\right ]\) peut être estimé (par exemple par méthode de Monte Carlo)
\(\nabla_{\boldsymbol\phi}ELBO(\boldsymbol x,\boldsymbol\theta,\boldsymbol\phi)\) est plus difficile à estimer (on ne peut rétropropager le gradient à travers \(\boldsymbol h\) pour calculer \(\nabla_{\boldsymbol\phi}\))
La solution à ce problème est appelée astuce de reparamétrisation (reparameterization trick) : on exprime \(\boldsymbol h\) à l’aide d’une transformation différentiable et inversible \(F\) d’une autre variable aléatoire \(\varepsilon\), étant donnés \(\boldsymbol x\) et \(\boldsymbol\phi\), de telle sorte que la distribution de \(\varepsilon\) est indépendante de \(\boldsymbol x\) et \(\boldsymbol\phi\) :
Un choix classique est
On montre alors que \(\nabla_{\boldsymbol\phi}ELBO(\boldsymbol x,\boldsymbol\theta,\boldsymbol\phi)\) peut être estimé par méthode de Monte Carlo.
Exemple#
Soit \(\boldsymbol h\in\mathbb{R}^d\). On suppose que la distribution de la variable latente suit une loi normale centrée réduite \(p(\boldsymbol h) = \mathcal N(\boldsymbol 0,\boldsymbol I)\).
Alors
où on modélise le décodeur \(D_{\boldsymbol\theta}\) par :
\(\boldsymbol\mu_{\boldsymbol\theta}(\boldsymbol h) = \boldsymbol W_1^\top \boldsymbol z + \boldsymbol b_1\)
\(log(\boldsymbol\sigma^2_{\boldsymbol\theta}(\boldsymbol h)) = \boldsymbol W_2^\top \boldsymbol z + \boldsymbol b_2\)
\(\boldsymbol z = ReLU(\boldsymbol W_3^\top \boldsymbol h + \boldsymbol b_3)\)
avec donc \(\boldsymbol\theta = (\boldsymbol W_1,\boldsymbol W_2,\boldsymbol W_3,\boldsymbol b_1,\boldsymbol b_2,\boldsymbol b_3)\)
De même, on modélise l’encodeur \(E_{\boldsymbol\phi}\) par :
où
\(p(\varepsilon) = \mathcal N(\boldsymbol 0,\boldsymbol I)\)
\(\boldsymbol h = \boldsymbol\mu_{\boldsymbol\phi}(\boldsymbol x) + \sigma_{\boldsymbol\phi}(\boldsymbol x)\odot\varepsilon\)
\(\boldsymbol\mu_{\boldsymbol\phi}(\boldsymbol x) = \boldsymbol W_4^\top \boldsymbol z + \boldsymbol b_4\)
\(log(\boldsymbol\sigma^2_{\boldsymbol\phi}(\boldsymbol x)) = \boldsymbol W_5^\top \boldsymbol z + \boldsymbol b_5\)
\(\boldsymbol z = ReLU(\boldsymbol W_6^\top \boldsymbol x + \boldsymbol b_6)\)
avec donc \(\boldsymbol\phi = (\boldsymbol W_4,\boldsymbol W_5,\boldsymbol W_6,\boldsymbol b_4,\boldsymbol b_5,\boldsymbol b_6)\)
Le calcul de ELBO est alors
où
dont les dérivées peuvent être évaluées analytiquement.
En résumé#
Pour utiliser un VAE il suffit donc
de définir l’encodeur et le décodeur
de définir la distribution de l’espace latent en utilisant l’astuce de reparamétrisation
de définir la fonction de perte ELBO
d’entraîner le tout et d’apprécier les données générées !
Implémentation#
On propose ici d’implémenter un auto-encodeur variationnel, et une variation de ce modèle intégrant une génération conditionnelle. Le jeu de données utilisé est Fashion MNIST.
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
from torchvision import transforms
On se donne des fonctions d’affichage des images reconstruites et générées.
def show(img):
plt.imshow(np.transpose(img.numpy(), (1,2,0)), interpolation='nearest')
# Affichage d'images reconstruites
def plot_reconstruction(model, n=24):
x,_ = next(iter(data_loader))
x = x[:n,:,:,:].to(device)
try:
out, _, _, log_p = model(x.view(-1, image_size))
except:
out, _, _ = model(x.view(-1, image_size))
x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim=3)
out_grid = torchvision.utils.make_grid(x_concat).cpu().data
show(out_grid)
# Affichage d'images générées par le VAE classique
def plot_generation(model, n=24):
with torch.no_grad():
z = torch.randn(n, z_dim).to(device)
out = model.decode(z).view(-1, 1, 28, 28)
out_grid = torchvision.utils.make_grid(out).cpu()
show(out_grid)
# Affichage d'images générées par le VAE où la génération est conditionnée par la classe.
def plot_conditional_generation(model, n=8):
plt.figure()
with torch.no_grad():
matrix = np.zeros((n,n_classes))
matrix[:,0] = 1
final = matrix[:]
for i in range(1,n_classes):
final = np.vstack((final,np.roll(matrix,i)))
z = torch.randn(8, z_dim)
z = z.repeat(n_classes,1).to(device)
y_onehot = torch.tensor(final).type(torch.FloatTensor).to(device)
out = model.decode(z,y_onehot).view(-1, 1, 28, 28)
out_grid = torchvision.utils.make_grid(out).cpu()
show(out_grid)
On charge ensuite les données
data_dir = 'data'
trainbatch_size = 128
testbatch_size = 16
dataset = torchvision.datasets.FashionMNIST(root=data_dir,train=True,transform=transforms.ToTensor(),download=True)
data_loader = torch.utils.data.DataLoader(dataset=dataset,batch_size=trainbatch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(torchvision.datasets.FashionMNIST(data_dir, train=False, download=True, transform=transforms.ToTensor()),batch_size=testbatch_size, shuffle=False)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
VAE classique#
On construit tout d’abord un VAE classique
image_size = 784
h_dim = 400
z_dim = 20
num_epochs = 15
learning_rate = 1e-3
class VAE(nn.Module):
def __init__(self, image_size=784, h_dim=400, z_dim=20):
super(VAE, self).__init__()
self.fc1 = nn.Linear(image_size, h_dim)
self.fc2 = nn.Linear(h_dim, z_dim)
self.fc3 = nn.Linear(h_dim, z_dim)
self.fc4 = nn.Linear(z_dim, h_dim)
self.fc5 = nn.Linear(h_dim, image_size)
def encode(self, x):
h = F.relu(self.fc1(x))
return self.fc2(h), self.fc3(h)
# Astuce de reparamétrisation
def reparameterize(self, mu, log_var):
std = torch.exp(log_var/2)
eps = torch.randn_like(std)
return mu + eps * std
def decode(self, z):
z = F.relu(self.fc4(z))
return torch.sigmoid(self.fc5(z))
def forward(self, x):
mu, log_var = self.encode(x)
h = self.reparameterize(mu, log_var)
x_reconst = self.decode(h)
return x_reconst, mu, log_var
model = VAE().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
On entraîne ensuite ce modèle
Recon = []
KL = []
for epoch in range(num_epochs):
for i,(x, _) in enumerate(data_loader):
x = x.to(device).view(-1, image_size)
x_reconst, mu, log_var = model(x)
reconst_loss = F.mse_loss(x_reconst, x, reduction='sum')
kl_div = - 0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
loss = reconst_loss + kl_div
if i%10==0:
Recon.append( reconst_loss.item()/len(x))
KL.append(kl_div.item()/len(x))
optimizer.zero_grad()
loss.backward()
optimizer.step()
plt.plot(Recon,color='r',label='Reconstruction Loss')
plt.plot(KL,color='b',label='Divergence KL')
plt.legend(loc='best')
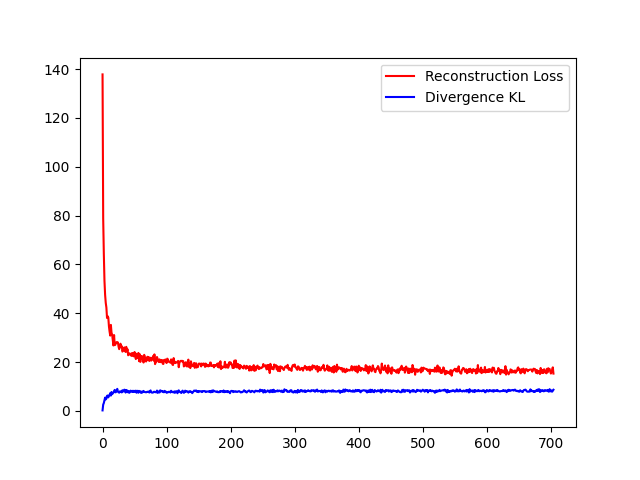
Fig. 64 Apprentissage du VAE#
On affiche alors des exemples d’images reconstruites
plot_reconstruction(model)

Fig. 65 Exemples d’images reconstruites \(\hat x = D(E(x))\)#
et des exemples d’images générées
plot_generation(model)
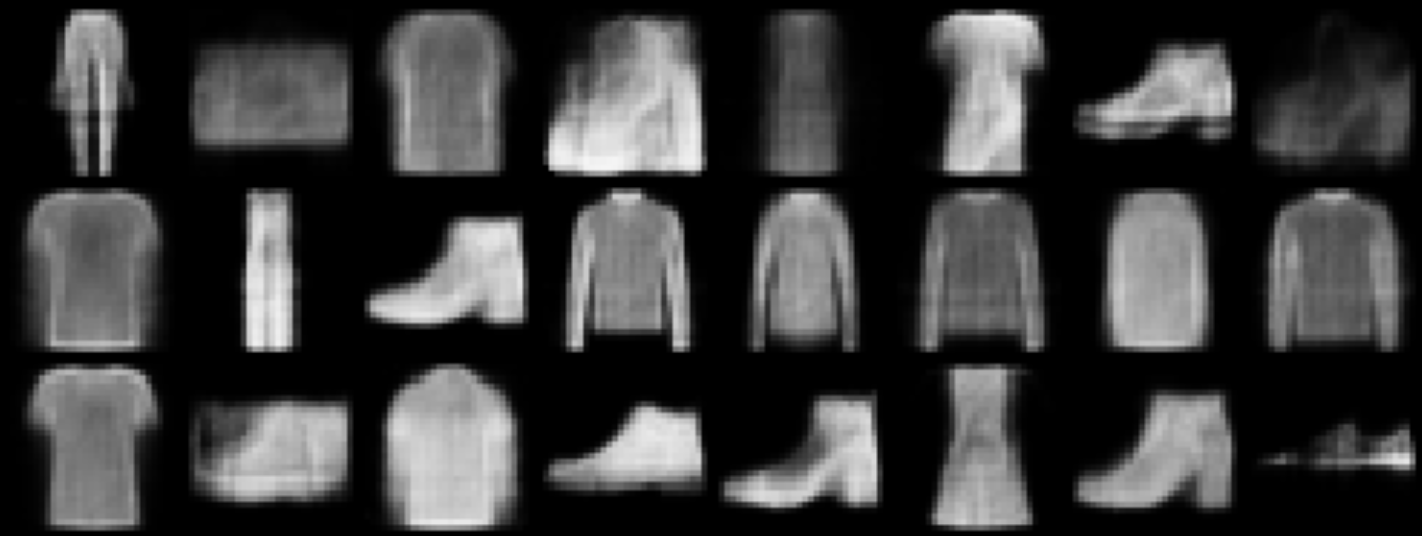
Fig. 66 Exemples d’images générées \(x=D(h)\)#
Le nombre d’epoches est faible, la génération n’est pas optimale.
VAE conditionnel#
On modifie légèrement l’architecture précédente en ajoutant l’information du label de l’exemple au décodeur. Pour cela il faut d’abord encoder le label (en one-hot)
n_classes = 10
def l_2_onehot(labels,nb_classes=n_classes):
l_onehot = torch.FloatTensor(labels.shape[0], n_classes)
l_onehot.zero_()
l_onehot.scatter_(1, labels.unsqueeze(1), 1)
return l_onehot
On modifie ensuite l’architecture précédente
class VAE_Cond(nn.Module):
def __init__(self, image_size=784, h_dim=400, z_dim=20, n_classes = 10):
super(VAE_Cond, self).__init__()
self.fc1 = nn.Linear(image_size, h_dim)
self.fc2 = nn.Linear(h_dim, z_dim)
self.fc3 = nn.Linear(h_dim, z_dim)
self.fc4 = nn.Linear(z_dim+n_classes, h_dim)
self.fc5 = nn.Linear(h_dim, image_size)
def encode(self, x):
h = F.relu(self.fc1(x))
return self.fc2(h), self.fc3(h)
def reparameterize(self, mu, log_var):
std = torch.exp(log_var/2)
eps = torch.randn_like(std)
return mu + eps * std
def decode(self, z, l_onehot):
# Concaténation de l'information de classe à la variable latente
x = torch.cat([z, l_onehot], 1)
z = F.relu(self.fc4(x))
return torch.sigmoid(self.fc5(z))
def forward(self, x, l_onehot):
mu, log_var = self.encode(x)
h = self.reparameterize(mu, log_var)
x_reconst = self.decode(h,l_onehot)
return x_reconst, mu, log_var
et on entraîne. Ici \(\beta\) permet de mettre à l’échelle la KL-divergence (voir \(\beta\)-VAE)
def train_C(model, data_loader=data_loader,num_epochs=num_epochs, beta=10., verbose=True):
model.train(True)
for epoch in range(num_epochs):
for i, (x, labels) in enumerate(data_loader):
x = x.to(device).view(-1, image_size)
l_onehot = l_2_onehot(labels)
l_onehot = l_onehot.to(device)
labels = labels.to(device)
x_reconst, mu, log_var = model(x,l_onehot)
reconst_loss = F.mse_loss(x_reconst, x, reduction='sum')
kl_div = - 0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
loss = reconst_loss + beta*kl_div
optimizer.zero_grad()
loss.backward()
optimizer.step()

Fig. 67 Exemples d’images générées \(x=D(h,c)\)#