Perceptron#

Définitions#

Definition 1 (Neurone)

Un neurone est une fonction non linéaire, paramétrée à valeurs bornées. Les \(D\) variables sur lesquelles opère le neurone sont habituellement désignées sous le terme d’entrées du neurone (notées \(x_i,i\in[\![1,D]\!])\), et la valeur de la fonction sous celui de sortie \(y\).
Le neurone formel calcule la sortie selon la formule :

\[y = f(w_0+\displaystyle\sum_{i=1}^Dw_ix_i) = f(w_0+\mathbf w^\top \mathbf x)\]

où :

  • \(\mathbf w = (w_1\cdots w_D)^\top\) est le vecteur des poids synaptiques qui pondèrent les entrées du neurone,

  • \(w_0\) est un biais

  • \(\mathbf w^\top \mathbf x\) est le potentiel du neurone

  • \(f\) est la fonction d’activation associée au neurone.

Definition 2 (Réseau de neurones)

Un réseau de neurones est un ensemble de neurones interconnectés. Les réseaux de neurones peuvent être visualisés par l’intermédiaire d’un graphe orienté. Chaque neurone est un noeud, les neurones étant connectés par des arêtes.

On distingue habituellement neurone d’entrée et neurone de sortie. Un neurone d’entrée calcule \(y = x\) où \(x\) est une entrée unique du neurone. Les neurones de sortie prennent un nombre quelconque d’entrées. Interconnectés, l’ensemble de ces neurones calcule \(\mathbf y(x)\) dont la dimension est donnée par le nombre de neurones d’entrée et de sortie (l’entrée du réseau est acceptée par les neurones d’entrée, qui forment la rétine), et la sortie du réseau est formée par les neurones de sortie.

Le cas le plus simple est celui d’un réseau comportant un seul neurone de sortie. C’est le perceptron. Le perceptron est un modèle de réseau de neurones avec algorithme d’apprentissage (Rosenblatt en 1958). L’idée sous-jacente de ce modèle est le fonctionnement de la rétine, l’étude de la perception visuelle. Nous commençons par aborder le cas du perceptron linéaire à seuil.

Definition 3 (Perceptron linéire à seuil)

Un perceptron linéaire à seuil prend en entrée \(D\) valeurs \(x_1\cdots x_D\) (la rétine) et calcule une sortie \(y\). Suivant la définition précédente, un perceptron est défini par la donnée de \(D+1\) constantes : les poids synaptiques \(w_1,\cdots,w_D\) et un seuil (ou le biais) \(\theta\). La sortie \(y\) est calculée par

\[\begin{split}y= \left \{ \begin{array}{lr} 1 & \textrm{si}\quad w^Tx=\displaystyle\sum_{i=1}^Dw_ix_i>\theta\\ 0 & \textrm{sinon}\\ \end{array} \right.\end{split}\]

Les entrées \(x_1,\cdots x_D\) peuvent être à valeurs dans {0,1} (ou {-1,1}) ou réelles, les poids peuvent être entiers ou réels.

Pour simplifier les notations et certaines preuves, on remplace souvent le seuil par un poids supplémentaire \(w_0\) associé à une entrée \(x_0=1\). L’équivalence entre le modèle avec seuil et le modèle avec entrée supplémentaire à 1 est immédiate : le coefficient \(w_0\) est l’opposé du seuil \(\theta\).

On note \(\mathbf w\) (respectivement \(\mathbf x\)) \(\in\mathbb R^{D+1}\) le vecteur des poids (resp. des entrées), augmenté de \(w_0\) (resp. \(x_0\)=1). Comme suggéré par la définition, on peut décomposer le calcul de la sortie \(y\) en un premier calcul de la quantité \(\mathbf w^T\mathbf x=\displaystyle\sum_{i=0}^Dw_ix_i\) appelée potentiel post-synaptique ou entrée totale, suivi d’une application d’une fonction d’activation sur cette entrée totale. Dans le cas du perceptron linéaire à seuil, la fonction d’activation est la fonction de Heaviside définie par \(f(x)=1_{\{x>0\}}\) lorsque la sortie est en {0,1}, et \(g(x) = 2f(x) - 1\) lorsque la sortie est en {-1,1}.

Utilisation : discrimination linéaire#

Soit \({\cal E}_a\) un ensemble d’exemples dans \(\mathbb R^D\times\){0,1} . On note

\[{\cal E}_a^0=\{\mathbf x\in \mathbb R^D/(\mathbf x,0)\in {\cal E}_a\}\textrm{ et } {\cal E}_a^1=\{\mathbf x\in \mathbb R^D/(\mathbf x,1)\in {\cal E}_a\}\]

On dit que \({\cal E}_a\) est linéairement séparable s’il existe un hyperplan \(H\) de \(\mathbb R^D\) tel que les ensembles \({\cal E}_a^0\) et \({\cal E}_a^1\) soient situés de part et d’autre de cet hyperplan.
On montre qu’un perceptron linéaire à seuil à \(D\) entrées divise l’espace des entrées \(\mathbb R^D\) en deux sous-espaces délimités par un hyperplan \(\mathbf w^T\mathbf x=-\theta\). Réciproquement, tout ensemble linéairement séparable peut être discriminé par un perceptron.
Un perceptron est donc un discriminant linéaire. On montre facilement qu’un échantillon de \(\mathbb R^D\) est séparable par un hyperplan si et seulement si l’échantillon de \(\mathbb R^{D+1}\) obtenu en rajoutant une entrée toujours égale à 1 est séparable par un hyperplan passant par l’origine.
Toute fonction de \(\mathbb R^D\) dans {0,1} n’est bien sur pas calculable par un tel perceptron.

Algorithme d’apprentissage par correction d’erreur#

Étant donné un échantillon d’apprentissage \({\cal E}_a\) de \(\mathbb R^D\times\) {0,1} (respectivement \(\{0,1\}^n\times\) {0,1}), c’est-à-dire un ensemble d’exemples dont les descriptions sont \(D\) attributs réels (respectivement binaires) et la classe est binaire, il s’agit de trouver un algorithme qui infère à partir de \({\cal E}_a\) un perceptron qui classifie correctement les éléments de \({\cal E}_a\) au vu de leurs descriptions si c’est possible, ou au mieux sinon.
L’algorithme d’apprentissage peut être décrit succinctement de la manière suivante. On initialise les poids du perceptron à des valeurs quelconques. A chaque fois que l’on présente un nouvel exemple, on ajuste les poids selon que le perceptron l’a correctement classé ou non. L’algorithme s’arrête lorsque tous les exemples ont été présentés sans modification d’aucun poids ou qu’un nombre maximum d’itération a été atteint.

Dans la suite, on note \(\mathbf{x_n}\) une entrée. La ième composante de \(\mathbf{x_n}\) est notée \(x_n^i\). Pour simplifier l’explication de l’algorithme, cette composante sera supposée binaire. Un échantillon \({\cal E}_a\) est un ensemble de couples \((\mathbf{x_n},t_n)\) où \(t_n\) est la classe binaire de \(\mathbf{x_n}\). Si une entrée \(\mathbf{x_n}\) est présentée en entrée d’un perceptron, on note \(y_n\) la sortie binaire calculée par le perceptron. Rappelons qu’il existe une \((D+1)^\textrm{ème}\) entrée \(x_0\) de valeur 1 pour le perceptron. L’apprentissage par correction d’erreur du perceptron est donné dans l”Algorithm 1

Algorithm 1 (Algorithme d’apprentissage du perceptron par correction d’erreur)

  1. Initialisation aléatoire des \(w_i\)

  2. Tant que (test)

    1. Prendre un exemple \((\mathbf{x_n},t_n)\) dans \({\cal E}_a\)

    2. Calculer la sortie \(y_n\) du perceptron pour l’entrée \(\mathbf{x_n}\)

    3. \((\forall i)\; w_i \leftarrow w_i+(t_n-y_n)x_n^i\)

La procédure d’apprentissage du perceptron est une procédure de correction d’erreur puisque les poids ne sont pas modifiés lorsque la sortie attendue \(t_n\) est égale à la sortie calculée \(y_n\) par le perceptron courant.

Étudions les modifications sur les poids lorsque \(t_n\) diffère de \(y_n\), lorsque \(\mathbf{x_n} \in \{0,1\}^D\) :

  • si \(y_n\)=0 et \(t_n\)=1, cela signifie que le perceptron n’a pas assez pris en compte les neurones actifs de l’entrée (c’est-à-dire les neurones ayant une entrée à 1). Dans ce cas, \(w_i \leftarrow w_i+x_n^i\) : l’algorithme ajoute la valeur de la rétine aux poids synaptiques (renforcement).

  • si \(y_n\)=1 et \(t_n\)=0, alors \(w_i \leftarrow w_i-x_n^i\) ; l’algorithme retranche la valeur de la rétine aux poids synaptiques (inhibition).

Remarquons que, en phase de calcul, les constantes du perceptron sont les poids synaptiques alors que les variables sont les entrées. Tandis que, en phase d’apprentissage, ce sont les coefficients synaptiques qui sont variables alors que les entrées de l’échantillon \({\cal E}_a\) apparaissent comme des constantes.
Certains éléments importants ont été laissés volontairement imprécis.

  • en premier lieu, il faut préciser comment est fait le choix d’un élément de \({\cal E}_a\) : aléatoirement ? En suivant un ordre prédéfini ? Doivent-ils être tous présentés ?

  • le critère d’arrêt de la boucle principale de l’algorithme n’est pas défini : après un certain nombre d’étapes ? Lorsque tous les exemples ont été présentés ? Lorsque les poids ne sont plus modifiés pendant un certain nombre d’étapes ?

Nous reviendrons sur toutes ces questions par la suite.

Example 1 (Apprentissage du OU binaire)

Les descriptions appartiennent à {0,1}\(^2\), les entrées du perceptron appartiennent à {0,1}\(^3\), la première composante correspond à l’entrée \(x_0\) et vaut toujours 1, les deux composantes suivantes correspondent aux variables \(x_1\) et \(x_2\) . On suppose qu’à l’initialisation, les poids suivants ont été choisis : \(w_0\)=0 ; \(w_1\) = 1 et \(w_2\) = -1. On suppose que les exemples sont présentés dans l’ordre lexicographique.

Le tableau suivant présente la trace de l’algorithme à partir de cette initialisation. Aucune entrée ne modifie le perceptron à partir de l’itération 10.

étape

\(w_0\)

\(w_1\)

\(w_2\)

Entrée

\(\mathbf w^\top \mathbf x\)

\(y\)

\(t\)

\(w_0\)

\(w_1\)

\(w_2\)

Init

0

1

-1

1

0

1

-1

100

0

0

0

0

1

-1

2

0

1

-1

101

-1

0

1

1

1

0

3

1

1

0

110

2

1

1

1

1

0

4

1

1

0

111

2

1

1

1

1

0

5

1

1

0

100

1

1

0

0

1

0

6

0

1

0

101

0

0

1

1

1

1

7

1

1

1

110

2

1

1

1

1

1

8

1

1

1

111

3

1

1

1

1

1

9

1

1

1

100

1

1

0

0

1

1

10

0

1

1

101

1

1

1

0

1

1

On peut montrer que si l’échantillon \({\cal E}_a\) est linéairement séparable et si les exemples sont présentés de manière équitable (c’est-à-dire que la procédure de choix des exemples n’en exclut aucun), la procédure d’apprentissage par correction d’erreur converge vers un perceptron linéaire à seuil qui sépare linéairement \({\cal E}_a\).

from IPython.display import Video
Video("videos/linsep.mp4",embed =True,width=700)

L’inconvénient majeur de cet apprentissage est que si l’échantillon présenté n’est pas linéairement séparable, l’algorithme ne convergera pas et l’on aura aucun moyen de le savoir.

from IPython.display import Video
Video("videos/nonlinsep.mp4",embed =True,width=700)

On pourrait penser qu’il suffit d’observer l’évolution des poids synaptiques pour en déduire si l’on doit arrêter ou non l’algorithme. En effet, si les poids et le seuil prennent deux fois les mêmes valeurs sans que le perceptron ait appris et alors que tous les exemples ont été présentés, cela signifie que l’échantillon n’est pas séparable. Et l’on peut penser que l’on peut borner les poids et le seuil en fonction de la taille de la rétine.

C’est vrai mais les résultats de complexité suivants montrent que cette idée n’est pas applicable en pratique.

  1. Toute fonction booléenne linéairement séparable sur \(D\) variables peut être réalisée par un perceptron dont les poids synaptiques entiers \(w_i\) sont tels que \(\left\lceil w_i\right\rceil \leq (D+1)^{\frac{D+1}{2}}\)

  2. Il existe des fonction booléennes linéairement séparables sur \(D\) variables qui requièrent des poids entiers supérieurs à \(2^{\frac{D+1}{2}}\)

Le premier résultat montre que l’on peut borner les poids synaptiques en fonction de la taille de la rétine, mais par un nombre tellement grand que toute application pratique de ce résultat semble exclue. Le second résultat montre en particulier que l’algorithme d’apprentissage peut nécessiter un nombre exponentiel d’étapes (en fonction de la taille de la rétine) avant de s’arrêter. En effet, les poids ne varient qu’au plus d’une unité à chaque étape. Même lorsque l’algorithme d’apprentissage du perceptron converge, rien ne garantit que la solution sera robuste, c’est-à-dire qu’elle ne sera pas remise en cause par la présentation d’un seul nouvel exemple. Pire encore, cet algorithme n’a aucune tolérance au bruit : si du bruit, c’est-à-dire une information mal classée, vient perturber les données d’entrée, le perceptron ne convergera jamais. En effet, des données linéairement séparables peuvent ne plus l’être à cause du bruit. En particulier, les problèmes non-déterministes, c’est-à-dire pour lesquels une même description peut représenter des éléments de classes différentes, ne peuvent pas être traités à l’aide d’un perceptron.

Algorithme d’apprentissage par descente de gradient#

Plutôt que d’obtenir un perceptron qui classifie correctement tous les exemples, il s’agit maintenant de calculer une erreur et d’essayer de minimiser cette erreur. Pour introduire cette notion d’erreur, on utilise des poids réels et donc des sorties réelles.

Un perceptron linéaire prend en entrée un vecteur \(\mathbf x_n\) et calcule une sortie \(y_n\). Un perceptron est défini par la donnée d’un vecteur \(\mathbf w\) de coefficients synaptiques. La sortie \(y_n\) est définie par \(y_n=\mathbf w^\top\mathbf x_n\). L’erreur du perceptron sur un échantillon d’apprentissage \({\cal E}_a\) d’exemples \((\mathbf x_n,t_n)\) est définie en utilisant par l’erreur quadratique

\[E(\mathbf w)=\frac{1}{2}\displaystyle\sum_{(\mathbf x_n,t_n)\in {\cal E}_a} (t_n-y_n)^2\]

L’erreur mesure donc l’écart entre les sorties attendue et calculée sur l’échantillon complet. On remarque que \(E(\mathbf w) = 0\) si et seulement si le perceptron classifie correctement l’échantillon complet. On suppose \({\cal E}_a\) fixé, le problème est donc de déterminer, par descente de gradient, un vecteur \(\tilde{\mathbf w}\) qui minimise \(E(\mathbf w)\). On a alors :

\[\begin{split}\begin{aligned} \frac{\partial E(\mathbf w)}{\partial w_i}&=\frac{\partial}{\partial w_i}\left (\frac{1}{2}\displaystyle\sum_{(\mathbf x_n,t_n)\in {\cal E}_a} (t_n-y_n)^2 \right )\\ &=\frac{1}{2}\displaystyle\sum_{{\cal E}_a}\frac{\partial}{\partial w_i}(t_n-y_n)^2\\ &=\displaystyle\sum_{{\cal E}_a}(t_n-y_n)\frac{\partial}{\partial w_i}(t_n-\mathbf w^\top \mathbf x_n)\\ &=\displaystyle\sum_{{\cal E}_a}(t_n-y_n)(-x_n^i)\\ \end{aligned}\end{split}\]

L’application de la méthode du gradient invite donc à modifier le poids \(w_i\) après une présentation complète de \({\cal E}_a\) d’une quantité \(\Delta w_i\) définie par : $\(\Delta w_i=-\epsilon \frac{\partial E(\mathbf w)}{\partial w_i}\)$

L’algorithme d’apprentissage par descente de gradient du perceptron linéaire peut maintenant être défini l”Algorithm 2.

Algorithm 2 (Algorithme d’apprentissage du perceptron par descente de gradient)

  1. Initialisation aléatoire des \(w_i\)

  2. Tant que (test)

    1. Pour tout \(i\) \(\Delta w_i \leftarrow 0\)

    2. Pour tout \((\mathbf x_n,t_n)\in {\cal E}_a\)

      1. Calculer \(y_n\)

      2. Pour tout \(i\) \(\Delta w_i \leftarrow \Delta w_i+\varepsilon (t_y-y_n)x_n^i\)

    3. Pour tout \(i\) \(w_i \leftarrow w_i + \Delta w_i\)

La fonction erreur quadratique ne possède qu’un minimum (la surface est une paraboloïde). La convergence est assurée, même si l’échantillon d’entrée n’est pas linéairement séparable, vers un minimum de la fonction erreur pour un \(\epsilon\) bien choisi, suffisamment petit. \(\varepsilon\) est appelé le taux d’apprentissage (ou learning rate).

Si \(\varepsilon\) est trop grand, on risque d’osciller autour du minimum. Pour cette raison, une modification classique est de diminuer graduellement la valeur de \(\varepsilon\) en fonction du nombre d’itérations. Le principal défaut est que la convergence peut être très lente et que chaque étape nécessite le calcul sur tout l’ensemble d’apprentissage.
Au lieu de calculer les variations des poids en sommant sur tous les exemples de \({\cal E}_a\), l’idée est alors de modifier les poids à chaque présentation d’exemple. La règle de modification des poids devient : $\(\Delta w_i=\varepsilon (t_n-y_n)x_n^i\)$

Cette règle est appelée règle delta, ou règle Adaline, ou encore règle de Widrow-Hoff, et l”Algorithm 3 décrit cette règle :

Algorithm 3 (Algorithme d’apprentissage du perceptron par descente de gradient)

  1. Initialisation aléatoire des \(w_i\)

  2. Tant que (test)

    1. Prendre un exemple \((\mathbf x_n,t_n)\in {\cal E}_a\)

    2. Calculer \(y_n\)

    3. Pour tout \(i\) \(w_i \leftarrow w_i+\varepsilon (t_y-y_n)x_n^i\)

En général, on parcourt l’échantillon dans un ordre prédéfini. Le critère d’arrêt généralement choisi fait intervenir un seuil de modifications des poids pour un passage complet de l’échantillon.\

Au coefficient \(\varepsilon\) près dans la règle de modification des poids, on retrouve l’algorithme d’apprentissage par correction d’erreur. Pour l’algorithme de Widrow-Hoff, il y a correction chaque fois que la sortie totale (qui est un réel) est différente de la valeur attendue. Ce n’est donc pas une méthode d’apprentissage par correction d’erreur puisqu’il y a modification du perceptron dans (presque) tous les cas. Rappelons également que l’algorithme par correction d’erreur produit en sortie un perceptron linéaire à seuil alors que l’algorithme par descente de gradient produit un perceptron linéaire. L’avantage de l’algorithme de Widrow-Hoff par rapport à l’algorithme par correction d’erreur est que, même si l’échantillon d’entrée n’est pas linéairement séparable, l’algorithme va converger vers une solution optimale (sous réserve du bon choix du paramètre \(\varepsilon\)). L’algorithme est, par conséquent, plus robuste au bruit.

L’algorithme de Widrow-Hoff s’écarte de l’algorithme du gradient sur un point important : on modifie les poids après présentation de chaque exemple en fonction de l’erreur locale et non de l’erreur globale. On utilise donc une méthode de type gradient stochastique. Rien ne prouve alors que la diminution de l’erreur en un point ne va pas être compensée par une augmentation de l’erreur pour les autres points. La justification empirique de cette manière de procéder est commune à toutes les méthodes adaptatives : le champ d’application des méthodes adaptatives est justement l’ensemble des problèmes pour lesquels des ajustements locaux vont finir par converger vers une solution globale.

L’algorithme de Widrow-Hoff est souvent utilisé en pratique et donne de bons résultats. Iil sera utilisé dans les autres réseaux de neurones rencontrés dans ce cours, avec sa variante où la modification des poids se fait après présentation d’un sous ensemble de données d’apprentissage (apprentissage par batchs). La convergence est, en général, plus rapide que par la méthode du gradient. Il est fréquent pour cet algorithme de faire diminuer la valeur de \(\varepsilon\) en fonction du nombre d’itérations comme pour l’algorithme du gradient.

Implémentation#

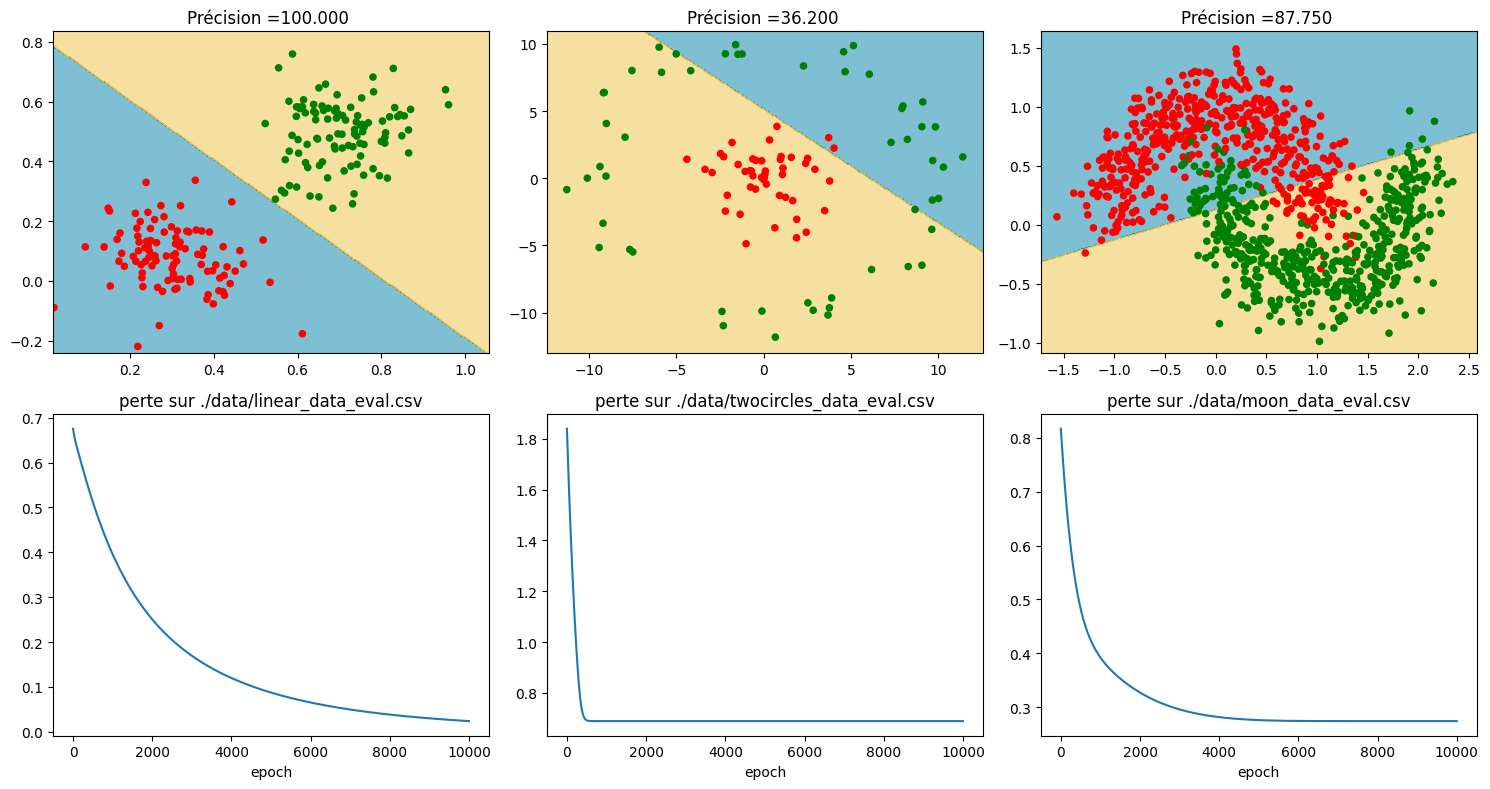
On illustre le pouvoir de séparation linéaire d’un perceptron sur trois jeux de données :

  • un jeu de données linéairement séparable

  • deux jeux de données non linéairement séparables classiques (« twocircles » et « moons »)

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import colors
import torch
import torch.nn as nn
import torch.optim as optim

fichiers_train = ['./data/linear_data_train.csv','./data/twocircles_data_train.csv','./data/moon_data_train.csv']
fichiers_test = ['./data/linear_data_eval.csv','./data/twocircles_data_eval.csv','./data/moon_data_eval.csv']

# Fonction de lecture des jeux de données
def extract_data(filename):

    labels = []
    features = []

    for line in open(filename):
        row = line.split(",")
        labels.append(int(row[0]))
        features.append([float(x) for x in row[1:]])

    features_np = np.matrix(features).astype(np.float32)

    labels_np = np.array(labels).astype(dtype=np.uint8)
    labels_onehot = (np.arange(num_labels) == labels_np[:, None]).astype(np.float32)

    return features_np,labels_onehot

On écrit une fonction permettant de visualiser le résultat de la classification par le perceptron.

def plotResults(ax,ay,X,Y,model,title,pltloss,name):
    mins = np.amin(X,0); 
    mins = mins - 0.1*np.abs(mins);
    maxs = np.amax(X,0); 
    maxs = maxs + 0.1*maxs;

    xs,ys = np.meshgrid(np.linspace(mins[0,0],maxs[0,0],300),np.linspace(mins[0,1], maxs[0,1], 300));

    toto = torch.FloatTensor(np.c_[xs.flatten(), ys.flatten()])
    Z = np.argmax(model(toto).detach().numpy(), axis=-1)
    Z=Z.reshape(xs.shape[0],xs.shape[1])
    
    labelY = np.matrix(Y[:, 0]+2*Y[:, 1])
    labelY = labelY.reshape(np.array(X[:, 0]).shape)

    ax.contourf(xs, ys, Z, cmap=colors.ListedColormap([[0,0.5,0.66,0], [0.93,0.76,0.27,0]]),alpha=.5)
    ax.scatter(np.array(X[:, 0]),np.array(X[:, 1]),c= np.array(labelY),s=20,cmap=colors.ListedColormap(['red', 'green']))
    ax.set_title(title)

    ay.plot(pltloss)
    ay.set_title("perte sur " + name)
    ay.set_xlabel("epoch")

    plt.tight_layout()

On construit ensuite le perceptron (extension de la classe nn.Module)

# Paramètres de l'apprentissage
batch_size = 100  
num_epochs = 10000
num_labels = 2 
num_features = 2

class Perceptron(nn.Module):
    def __init__(self,p):
        super(Perceptron, self).__init__()
        # Couche d'entrée
        self.fc = nn.Linear(num_features,num_labels)
        self.output = nn.Softmax(1) 
    def forward(self, x):
        lin = self.fc(x)
        output = self.output(lin) 
        return output

On écrit ensuite la fonction d’entraînement. La fonction de perte est l”entropie croisée binaire et l’optimiseur est Adam .

loss = nn.BCELoss()

def train_session(X,y,classifier,criterion,optimizer,n_epochs=num_epochs):
    loss_values = []    
    losses = np.zeros(n_epochs)
    correct = 0
    for iter in range(n_epochs):
        optimizer.zero_grad() 
        yPred = classifier(X)
        loss = criterion(yPred,y)
        loss_values.append(loss.detach().numpy())
        #Gradient et rétropropagation
        loss.backward()
        #Mise à jour des poids
        optimizer.step()
        y2 = yPred>0.5
        correct = (y2 == y).sum().item()/2
    acc = 100 * correct / (X.shape[0])
    return loss_values,acc

On applique enfin le perceptron sur les jeux de données et on visualise les résultats.

fig,axs = plt.subplots(2, 3,figsize=(15,8))
for i,name_train,name_test in zip ([0,1,2],fichiers_train,fichiers_test):
    train_data,train_labels = extract_data(name_train)
    test_data, test_labels = extract_data(name_test)

    model = Perceptron(train_data.shape[1])
    optimizer = optim.Adam(model.parameters())
    pltloss,acc = train_session(torch.FloatTensor(train_data),torch.FloatTensor(train_labels),model,loss,optimizer)
    
    titre= "Précision ={0:5.3f} ".format(acc)
    plotResults(axs[0][i],axs[1][i],test_data, test_labels, model, titre, pltloss, name_test)
_images/0f3bc762edc3e36e1580f1737643cb05615c486483c762a126125d7203380efb.png

Pour en finir avec le perceptron#

L’apprentissage par correction ou par la méthode du gradient ne sont rien d’autre que des techniques de séparation linéaire qu’il faudrait comparer aux techniques utilisées habituellement en statistiques (discriminant linéaire, machines à vecteurs de support,…). Ces méthodes sont non paramétriques, c’est-à-dire qu’elles n’exigent aucune autre hypothèse sur les données que la séparabilité.

On peut montrer que presque tous les échantillons de moins de \(2D\) exemples sont linéairement séparables lorsque \(D\) est le nombre de variables. Une classification correcte d’un petit échantillon n’a donc aucune valeur prédictive. Par contre, lorsque l’on travaille sur suffisamment de données et que le problème s’y prête, on constate empiriquement que le perceptron appris par un des algorithmes précédents a un bon pouvoir prédictif.

Il est bien évident que la plupart des problèmes d’apprentissage qui se posent naturellement ne peuvent pas être résolus par des méthodes aussi simples : il n’y a que très peu d’espoir que les exemples naturels se répartissent sagement de part et d’autre d’un hyperplan. Deux manières de résoudre cette difficulté peuvent être envisagées :

  • soit mettre au point des séparateurs non-linéaires,

  • soit (ce qui revient à peu près au même) complexifier l’espace de représentation de manière à linéariser le problème initial.

Les réseaux multicouches abordent ce type de problème.