try:
import torch_geometric
except ModuleNotFoundError:
!pip3 install --quiet torch_geometric
import torch_geometric
Graph Neural Networks#
Comme leur nom l’indique, les Graph Neural Networks sont des réseaux de neurones qui traitent les graphes. Ce traitement pose trois problématiques :
leur topologie est variable, et il est difficile de concevoir des réseaux qui soient à la fois suffisamment expressifs et capables de gérer cette variation.
ils peuvent être de taille conséquente : un graphe représentant les connexions entre les utilisateurs d’un réseau social peut avoir plusieurs millions de sommets.
il se peut qu’il n’y ait à disposition pour le problème à traiter qu’un seul graphe, de sorte que le protocole habituel d’entraînement avec de nombreux exemples de données et de test avec de nouvelles données n’est pas toujours possible.
Représentation d’un graphe#
Définition matricielle d’un graphe#
Soit \(G=(V,E)\) un graphe à \(N=|V|\) sommets et \(M=|E|\) arcs (ou arêtes). Chaque sommet et chaque arc (ou arête) peut porter une information vectorielle (graphe pondéré). On choisit alors de représenter \(G\) par trois matrices \(\mathbf A,\mathbf X\) et \(\mathbf E\) représentant respectivement la struture de \(G\), les sommets et arcs (ou arêtes):
\(\mathbf A\) est la matrice d’adjacence (pour les arêtes) ou d’incidence (pour les arcs).
\(\mathbf X\) est une matrice de taille \(d\times N\), la \(i\)-eme colonne de \(\mathbf X\) donnant les \(d\) informations portées par le sommet \(i\in[\![1,N]\!]\).
\(\mathbf E\) est une matrice de taille \(d_e\times M\), la \(i\)-eme colonne de \(\mathbf E\) donnant les \(d_e\) informations portées par l’arc (ou l’arête) \(i\in[\![1,N]\!]\).
Dans un premier temps, on considérera uniquement le cas où \(\mathbf X\) existe (seuls les sommets sont pondérés). On reviendra sur le cas de \(\mathbf E\) plus tard.
Propriétés#
La matrice d’adjacence peut être utilisée pour trouver les voisins d’un sommet. Supposons que le \(i\)-eme sommet soit encodé sous la forme d’un vecteur colonne \(\mathbf X_{\bullet,i}\) avec une seule entrée non nulle à la position \(i\), fixée à un. En prémultipliant \(\mathbf X_{\bullet,i}\) par la matrice \(\mathbf A\), on calcule un vecteur avec des uns aux positions des voisins. En répétant cette procédure \(n\) fois, on accède aux voisins du sommet \(i\) accessibles en \(n\) étapes. Ainsi, le coefficient (l,c) de \(\mathbf A^n\) contient le nombre de chaînes uniques de longueur \(n\) du sommet \(l\) au sommet \(c\). A noter que ce n’est pas le nombre de chemins uniques puisqu’il inclut les chemins qui visitent le même sommet plus d’une fois. Les sommets étant numérotés arbitrairement dans \(G\), il est de plus possible de changer l’indexation de ces sommets, sans changer la struture de \(G\), à l’aide d’une matrice de permutation \(\mathbf P\). Les informations portées par les sommets sont alors résumées dans la matrice \(\mathbf X\mathbf P\), et la nouvelle matrice d’adjacence est donnée par \(\mathbf P^T\mathbf A \mathbf P\).
Introduction aux GNN#
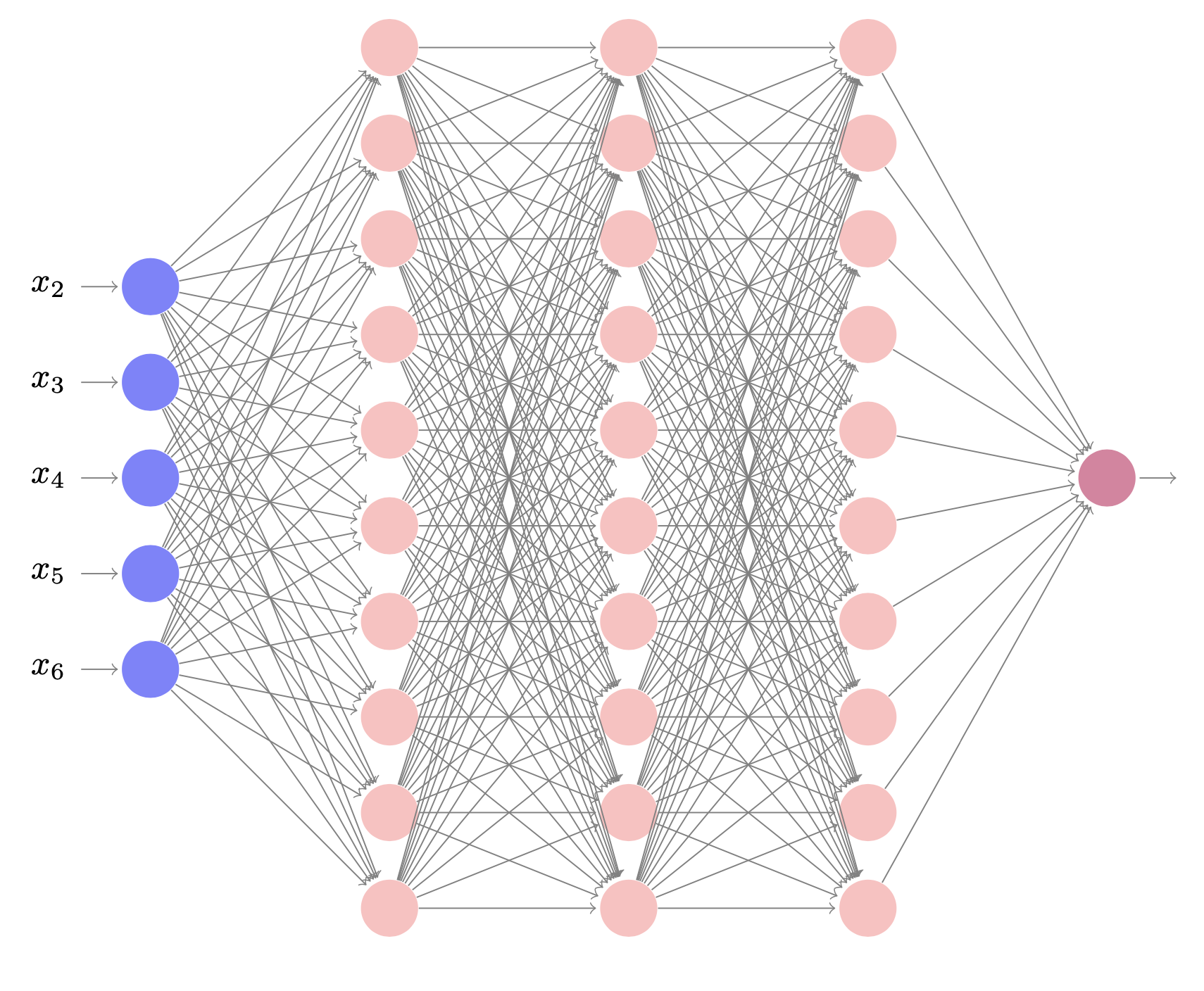
Un GNN est un modèle qui prend les représentations des sommets
\(\mathbf X\) et la matrice d’adjacence \(\mathbf A\) comme entrées et les
fait passer par une série de \(K\) couches. Les représentations des
sommets sont mises à jour à chaque couche pour créer des représentations
intermédiaires cachées \(\mathbf H_k\) avant de calculer les
représentations de sortie \(\mathbf H_K\), dont les colonnes comprennent
des informations sur les sommets correspondants et leur contexte dans
\(G\).
Les GNN peuvent être utilisés en exploitant la structure de \(G\), les sommets et/ou les arcs ou arêtes.
Utilisations#
En relation avec la structure de graphe#
Le réseau attribue une étiquette ou estime une ou plusieurs valeurs à partir de l’ensemble du graphe, en exploitant à la fois la structure et la représentation des sommets. Par exemple, on peut vouloir prédire la température à laquelle un gaz (molécules représentées sous la forme d’un graphe) devient liquide (régression) ou si une molécule est toxique ou non (classification). Les représentations des sommets de sortie sont combinées (par exemple, en calculant la moyenne) et le vecteur résultant est mis en correspondance avec un vecteur de taille fixe par le biais d’une transformation linéaire ou d’un réseau de neurones. Pour la régression, le décalage entre le résultat et les valeurs de vérité terrain est calculé à l’aide de la fonction de perte moindres carrés. Pour la classification binaire, la sortie passe par une fonction sigmoïde et la perte est calculée à l’aide de l’entropie croisée binaire
où \(\beta_K\) et \(\mathbf w_K^T\in\mathbb{R}^D\) sont des paramètres à apprendre. Multiplier à droite par le vecteur colonne \(\mathbf 1\) somme toutes les représentations, et diviser par \(N\) calcule la moyenne. La technique résultante est dite mean pooling.
En relation avec les sommets#
Le réseau attribue une étiquette (classification) ou une ou plusieurs valeurs (régression) à chaque sommet du graphe, en utilisant à la fois la structure du graphe et les représentations des sommets. Par exemple, dans un graphe construit à partir d’un nuage de points 3D d’un avion, l’objectif peut être de classer les sommets selon qu’ils appartiennent aux ailes ou au fuselage (classification). En régression, on peut par exemple vouloir prédire le nombre de messages qu’un abonné d’un réseau social recevra. Les fonctions de perte sont définies de la même manière que pour les tâches au niveau du graphe, sauf que cette opération est effectuée indépendamment pour chaque sommet i :
En relation avec les arcs ou arêtes#
Le réseau prédit s’il doit y avoir ou non un arc (ou arête) entre les sommets \(i\) et \(j\). Par exemple, dans le cadre d’un réseau social, le réseau peut prédire si deux personnes se connaissent et s’apprécient et suggérer qu’elles se connectent si c’est le cas. C’est une tâche de classification binaire pour laquelle la représentation des deux sommets doit être convertie en un nombre unique représentant la probabilité de présence de l’arc (ou arête). L’une des possibilités consiste à prendre le produit scalaire des représentations des sommets et à faire passer le résultat par une fonction sigmoïde pour calculer la probabilité.
GCN#
Il existe de nombreux types de GNN, on se restreint ici aux réseaux convolutifs de graphes, ou GCN. Ces modèles sont convolutifs en ce sens qu’ils mettent à jour chaque sommet en agrégeant les informations provenant des sommets voisins. En tant que tels, ils induisent un biais inductif relationnel (une tendance à donner la priorité aux informations provenant des voisins). On suppose de plus que les convolutions s’opèrent dans le domaine spatial (utilisant la structure de \(G\)), plutôt que dans l’espace de Fourier (méthodes basées spectre). Chaque couche du GCN est une fonction \(\mathbf F_{\boldsymbol \phi}\), de paramètres \({\boldsymbol \phi}\), qui prend en entrée les représentations des sommets \(\mathbf X\) et la matrice d’adjacence \(\mathbf A\) de \(G\) et produit de nouvelles représentations des sommets :
les \(\boldsymbol \phi_{k}\) étant les paramètres du réseau entre la couche \(k\) et la couche \(k+1\).
Equivariance et invariance#
L’indexation des sommets dans le graphe étant arbitraire, il est indispensable que tout modèle respecte cette propriété. Chaque couche doit donc être équivariante par rapport aux permutations des indices des sommets, soit pour toute permutation \(\mathbf P\) et tout \(k\):
Remark 1
Une fonction \(f\) est équivariante pour une transformation \(t\) si pour tout \(x, f(t(x)) = t(f(x))\)
Pour les tâches de classification des sommets et de prédiction des arcs ou arêtes, les résultats doivent également être équivariants pour les permutations des indices des sommets. Toutefois, pour les tâches en relation avec le graphe, la couche finale agrège les informations provenant de l’ensemble du graphe, de sorte que le résultat est invariant par rapport à l’ordre des sommets.
Partage des paramètres#
Dans les réseaux convolutifs, des couches convolutives sont utilisées, qui traitent chaque position de l’image de manière identique. Cela permet de réduire le nombre de paramètres et d’introduire un biais inductif qui force le modèle à traiter chaque partie de l’image de la même manière. Le même argument peut être avancé pour les sommets d’un graphe. On pourrait apprendre un modèle avec des paramètres distincts associés à chaque sommet. Cependant, le réseau doit maintenant apprendre indépendamment la signification des connexions dans le graphe à chaque position, et l’apprentissage nécessiterait de nombreux graphes ayant la même topologie. Il est plus judicieux de construire un modèle qui utilise les mêmes paramètres à chaque sommet, réduisant ainsi le nombre de paramètres et partageant ce que le réseau apprend à chaque sommet sur l’ensemble du graphe.
On peut modéliser une convolution (qui met à jour une variable en prenant une somme pondérée des informations provenant de ses voisins) comme le fait que chaque voisin envoie un message à la variable d’intérêt, qui agrège ces messages pour former la mise à jour. Dans le cas des images, les voisins sont les pixels d’une région carrée de taille fixe autour de la position actuelle, de sorte que les relations spatiales à chaque position sont les mêmes. Dans un graphe, chaque sommet peut avoir un nombre différent de voisins et il n’existe a priori pas de relation privilégiée entre sommets : il n’y a aucune raison de pondérer favorablement (ou pas) les informations provenant d’un sommet particulier.
Exemple#
La (Fig. 61) présente un exemple simple de GCN.
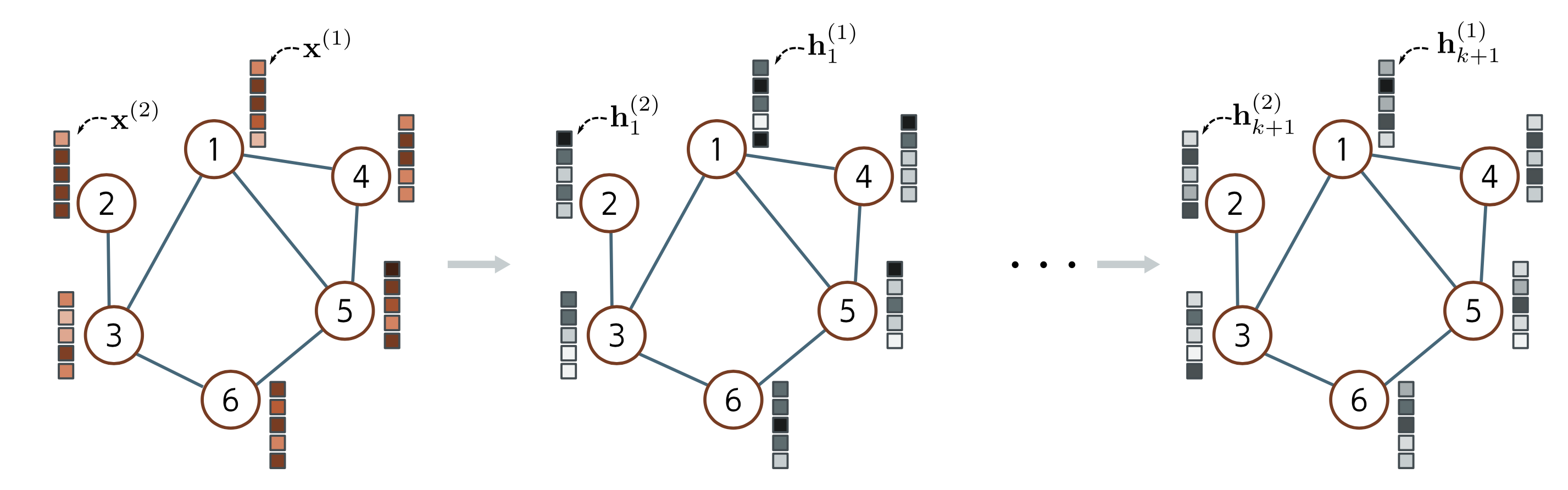
Fig. 61 Exemple de GCN#
à gauche le graphe \(G\) initial, les colonnes de \(\mathbf X\) étant reportées à côté des sommets correspondants.
au milieu, chaque sommet de la première couche cachée est mis à jour en :
agrégeant les sommets voisins d’un sommet \(i\) en un unique vecteur : \(\mathbf f_1(i) = \displaystyle\sum_{j\textrm{ voisin de }i} \mathbf h_1(j)\)
appliquant pour tout \(i\) une transformation linéaire \(\mathbf L\) au sommet initial \(\mathbf x^{i}\) et aux sommets agrégés et en ajoutant un biais \(\boldsymbol\beta_0\) : \(\boldsymbol \beta_0 + \mathbf L\mathbf x^{i} + \mathbf L \mathbf f_1(i)\)
appliquant une fonction non linéaire \(g\) au résultat précédent : \(\mathbf h_1^{i} =g(\boldsymbol \beta_0 + \mathbf L \mathbf x^{i} + \mathbf L f_1(i))\)
à droite, le processus répété pour toute couche \(k\) :
\[(\forall i)\; \; \mathbf h_{k+1}^{i} = g \left (\boldsymbol \beta_k+\mathbf L_k \mathbf h_k^{i} + \mathbf L_k\left (\displaystyle\sum_{j\textrm{ voisin de }i} \mathbf h_k(j)\right ) \right )\]
On peut écrire ce processus de manière matricielle : Si \(\mathbf H_k\in\mathcal{M}_{D,N}(\mathbb{R})\) est la matrice dont les colonnes sont les représentations des sommets, alors
où \(g\) est appliquée point à point sur les éléments de la matrice argument. On remarque que la couche \(k+1\) est bien équivariante à la permutation de la numérotation des sommets, utilise la structure du graphe (\(\mathbf A\)) pour produire un biais inductif et partage les paramètres sur tout le graphe.
Application en classification#
Pour l’exemple, on s’intéresse à un problème de classification binaire. On modélise une molécule comme un graphe, sont les sommets sont les atomes. La matrice \(\mathbf A\) donne les liaisons entre les atomes, et la matrice \(\mathbf X\) donne le nom de l’atome : si la table périodique des éléments comporte \(D\) atomes, le sommet (l’atome) \(i\) est un vecteur de \(\{0,1\}^D\), où la seule composante qui vaille 1 est celle qui identifie le type de l’atome. On s’intéresse alors de savoir si une molécule donnée est toxique (\(y=1\)) ou pas (\(y=0\)).
Les équations du réseau sont alors :
et
où \(\boldsymbol \phi=(\boldsymbol \beta_k,\mathbf L_k)_{k\in[\![0,K]\!]}\) sont les paramètres du réseau à apprendre et \(\sigma\) la fonction sigmoïde.
Étant donnés \(n\) exemples d’entraînement \((\mathbf X_i,\mathbf A_i,y_i)_{i\in[\![1,n]\!]}\), \(\boldsymbol \phi\) peut être classiquement appris par minimisation de l’entropie croisée binaire sur des batchs d’exemples. Si dans les MLP et les CNN, les entrées sont de taille identique (et donc les exemples sont concaténés en un tenseur de dimension supérieure pour un entraînement efficace par GPU ou TPU), les graphes de la base d’entraînement ont très probablement un nombre de sommets \(N\) et une dimension de l’espace de représentation \(D\) différents, ce qui rend cette concaténation impossible. Une astuce simple permet cependant de traiter l’ensemble du batch en parallèle. Les graphes du batch sont traités comme des composantes disjointes d’un seul grand graphe. Le réseau peut alors être exécuté comme une instance unique des équations de réseau. La mise en commun des moyennes est effectuée uniquement sur les graphes individuels afin d’obtenir une représentation unique par graphe qui peut être introduite dans la fonction de perte.
Modèles inductifs et transductifs#
Jusqu’à présent, tous les modèles présentés dans ce cours ont été inductifs : on exploite un ensemble de données étiquetées pour apprendre la relation entre les entrées et les sorties. On l’applique ensuite à de nouvelles données de test. En d’autres termes, on apprend la règle qui associe les entrées aux sorties, puis on l’applique ailleurs.
En revanche, un modèle transductif (ou apprentissage semi-supervisé) prend en compte les données étiquetées et non étiquetées en même temps. Il ne produit pas de règle, mais simplement une étiquette pour les sorties inconnues. Il présente l’avantage de pouvoir utiliser des modèles sur des données non étiquetées pour prendre ses décisions, mais nécessite un nouvel entraînement du modèle lorsque des données non étiquetées supplémentaires sont ajoutées.
Les deux types de problèmes sont couramment rencontrés pour les graphes. Parfois, on dispose de nombreux graphes étiquetés et on apprend une correspondance entre le graphe et les étiquettes. D’autres fois, il arrive qu’il n’y ait à disposition qu’un seul graphe de très grande dimension et dans ce cas, les données d’apprentissage et de test sont nécessairement connectées.
Les utilisations des GNN en relation avec la structure des graphes ne se produisent que dans le cadre inductif où il existe des graphes d’apprentissage et de test. Toutefois, les utilisations en relation avec les sommets et les tâches de prédiction des arcs ou arêtes peuvent se produire dans l’un ou l’autre cadre. Dans le cas transductif, la fonction de perte minimise le décalage entre la sortie du modèle et la vérité lorsqu’elle est connue. Les nouvelles prédictions sont calculées en exécutant la passe avant et en récupérant les résultats lorsque la vérité est inconnue.
Exemple en classification de sommets#
On s’intéresse ici à un problème de classification binaire des sommet dans un cadre transductif. Le graphe considéré comporte des millions de sommets, certains ayant des étiquettes binaires \(y_i\). L’objectif est alors d’étiqueter les sommets non étiquetés restants. Le réseau est le même que pour la classification binaire avec une couche finale différente qui produit un vecteur de sortie de taille \(1\times N\) :
la fonction \(\sigma\) agissant point à point. On trouve \(\boldsymbol \phi\) par minimisation de l’entropie croisée binaire, mais seulement à partir des valeurs des sommets pour lesquels les étiquettes \(y_i\) sont connues.
L’entraînement de ce réseau pose deux problèmes. Tout d’abord, il est difficile d’entraîner un réseau de cette taille, ne serait-ce que parce qu’il faut stocker les représentations des sommets à chaque couche du réseau dans la passe avant. Cela implique à la fois le stockage et le traitement d’une structure plusieurs fois plus grande que le graphe entier. De plus, n’ayant qu’un seul graphe à disposition, la descente de gradient (ou tout autre algorithme d’optimisation) sur batch est impossible, puisq’un seul objet constitue la base d’entraînement.
Pour répondre à ce second problème, on choisit un sous-ensemble aléatoire de sommets étiquetés à chaque étape de l’entraînement. Chaque sommet dépend de ses voisins dans la couche précédente. Ces derniers dépendent à leur tour de leurs voisins de la couche précédente, de sorte que chaque sommet possède l’équivalent d’un champ réceptif comme dans les CNN. La taille du champ réceptif est appelée voisinage à \(k\) sauts. On peut donc effectuer une étape de descente de gradient en utilisant le graphe qui forme l’union des voisinages de \(k\)-sauts des sommets du batch. Les entrées restantes ne contribuent pas. S’il y a de nombreuses couches et que le graphe est fortement connecté, chaque sommet d’entrée peut se trouver dans le champ réceptif de chaque sortie, ce qui ne réduit pas du tout la taille du graphe : c’est le problème de l’expansion du graphe. Deux approches s’attaquent à ce problème : l’échantillonnage du voisinage et le partitionnement du graphe.
Échantillonnage du voisinage#
Le graphe complet est échantillonné, ce qui réduit les connexions à chaque couche du réseau. Par exemple, on peut commencer par les sommets du batch et échantillonner aléatoirement un nombre fixe de leurs voisins dans la couche précédente. Ensuite, on échantillonne au hasard un nombre fixe de leurs voisins dans la couche précédente, et ainsi de suite. La taille du graphe augmente toujours à chaque couche, mais de manière beaucoup plus contrôlée. Cette opération est renouvelée pour chaque batch, de sorte que les voisins contributeurs diffèrent même si le même batch est tiré deux fois. Cette techique rappelle celle du dropout et ajoute une certaine régularisation.
Partitionnement du graphe#
On peut également partitionner le graphe original en sous-ensembles de sommet disjoints, et construire des graphes plus petits qui ne sont pas connectés les uns aux autres avant le traitement. Il existe des algorithmes standards pour choisir ces sous-ensembles afin de maximiser le nombre de liens internes. Ces petits graphes peuvent chacun être traités comme des batchs, ou un sous-ensemble aléatoire d’entre eux peut être combiné pour former un batch (en rétablissant toutes les arêtes entre eux à partir du graphe d’origine). Utilisant l’une de ces deux approches, il est alors possible d’entraîner les paramètres du réseau de la même manière que pour le cadre inductif, en divisant les sommets étiquetés en ensembles d’entrainement, de test et de validation comme souhaité. Pour effectuer l’inférence, on calcule les prédictions pour les sommets inconnus sur la base de leur voisinage de \(k\)-sauts. Contrairement à l’entraînement, il n’est pas nécessaire de stocker les représentations intermédiaires, ce qui rend l’utilisation de la mémoire beaucoup plus efficiente.
Couches d’un GNN#
les sections précédentes combinaient les sommets adjacents par sommation, en multipliant \(\mathbf H\) par \(\mathbf A+\mathbf I\). Dans la suite de ce paragraphe, on présente des alternatives à cette approche.
Amélioration de la diagonale#
La mise à jour proposée jusqu’à lors $\(\forall k\in[\![0,K-1]\!]\; \mathbf H_{k+1} = g\left (\boldsymbol\beta_k \mathbf 1^T + \mathbf L_k\mathbf H_k(\mathbf A+\mathbf I)\right )\)$
peut être modifiée en
où \(\epsilon_k\) est appris, ou en
où \(\mathbf L'_k=\begin{pmatrix}\mathbf L_k &\boldsymbol \psi_k\end{pmatrix}\) permet d’appliquer une transformation linéaire différente au sommet courant.
Connexions résiduelles#
Avec les connexions résiduelles, la représentation agrégée des voisins est transformée et passe par la fonction d’activation avant d’être additionnée ou concaténée avec le sommet actuel :
Agrégation moyenne#
Les méthodes précédentes regroupent les voisins en additionnant les représentation des sommets. Cependant, il est possible de combiner différemment ces représentations. Parfois, il est préférable de prendre la moyenne des voisins plutôt que la somme. Cette méthode peut s’avérer plus performante si les informations de représentation sont plus importantes et les informations structurelles moins, car la part de contribution du voisinage ne dépend pas du nombre de voisins :
où \(\mathcal{V}_i\) désigne l’ensemble des voisins du sommet \(i\). En notation matricielle, si \(\mathbf D\) est la matrice diagonale des degrés alors
Normalisation de Kipf#
Ici
l’information provenant des sommets ayant un grand nombre de voisins devant être revue à la baisse (il existe un grand nombre d’arcs qui fournissent moins d’information unique). En notation matricielle, cette normalisation s’écrit
Example 2
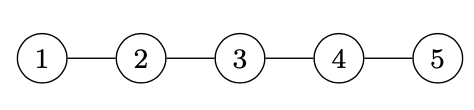
Chaque noeud \(i\in [\![1,5]\!]\) est décrit par \(\mathbf v_i\in\mathbb{R}^3\), \(d=3\)
\(\mathbf A+\mathbf I = \begin{pmatrix}1&1&0&0&0\\ 1&1&1&0&0\\ 0&1&1&1&0\\ 0&0&1&1&1\\ 0&0&0&1&1\end{pmatrix}\)
\(\mathbf D\): matrice \(N\times N\) des degrés de \(\mathbf A+\mathbf I\), \(\mathbf D = \begin{pmatrix}2&0&0&0&0\\ 0& 3&0&0&0\\ 0&0&3&0&0\\ 0&0&0&3&0\\ 0&0&0&0&2 \end{pmatrix}\)
\(\mathbf H_0=\begin{pmatrix} \mathbf v_1&\mathbf v_2&\mathbf v_3&\mathbf v_4&\mathbf v_5\end{pmatrix}\)
\(\mathbf L_0\): matrice \(2\times d\)
\(\boldsymbol\beta_0 \in\mathbb R^2\), \(\mathbf 1\in\mathbb R^N\)
\(\mathbf H_1= \left (\boldsymbol\beta_0 \mathbf 1^T + \mathbf L_0\mathbf H_0(\mathbf D^{-\frac12}\mathbf A\mathbf D^{-\frac12} + I)\right )\) matrice \(2\times N\) : représentation des noeuds à l’itération 1, avec
Agrégation par max pooling#
Comme dans le cas des CNN, on peut envisager d’agréger par le max, qui s’effectue alors composante par composante.
Agrégation par attention#
Les méthodes d’agrégation examinées jusqu’à présent pondèrent la contribution des voisins de manière égale ou d’une manière qui dépend de la topologie du graphe. Inversement, dans les couches d’attention de graphe, les poids dépendent des données aux sommets. Une transformation linéaire est appliquée aux représentations des sommets
La similarité \(s_{ij}\) entre les représentations transformées \(\mathbf h'_i, \mathbf h'_j\) des sommets \(i\) et \(j\) est calculée en concaténant les paires, en effectuant un produit scalaire avec un vecteur colonne \(\boldsymbol \phi_k\) de paramètres appris et en appliquant une fonction d’activation
Les similarités sont stockées dans une matrice \(\mathbf S\). Comme pour les mécanismes d’attention, les poids doivent être positifs et de somme 1, mais pour un sommet donné, seuls lui et ses voisins doivent contribuer. On effectue donc l’opération
la fonction \(\textrm{Softmax}(\bullet,\bullet)\) calcule les valeurs d’attention en appliquant l’opération softmax séparément à chaque colonne de son premier argument \(\mathbf S\), mais seulement après avoir fixé à \(-\infty\) les valeurs pour lesquelles le deuxième argument \(\mathbf A+\mathbf I\) est égal à zéro, de sorte qu’elles ne contribuent pas. Cela garantit que l’attention accordée aux sommets non voisins est nulle.
Prise en compte de l’information des arcs ou arêtes#
Les paragraphes précédents ont abordé le traitement des représentrations des sommets. Ceux-ci évoluent au fur et à mesure qu’ils sont transmis dans le réseau, de sorte qu’à la fin ils représentent à la fois le sommet et son contexte dans le graphe. On considère maintenant le cas où l’information est associée aux arêtes du graphe.
Il est facile d’adapter le mécanisme de représentation précédent pour traiter la représentation des arêtes à l’aide du graphe des arêtes (ou graphe adjoint). Il s’agit d’un graphe complémentaire, dans lequel chaque arête du graphe original devient un sommet, et chaque paire d’arêtes ayant un sommet commun dans le graphe original crée une arête dans le nouveau graphe. En général, un graphe peut être reconstruit à partir de son graphe d’arêtes, de sorte qu’il est possible de passer d’une représentation à l’autre.
Une fois le graphe d’arêtes construit, on utilise les mêmes techniques, en agrégeant les informations de chaque nouveau sommet à partir de ses voisins et en les combinant avec la représentation actuelle. Lorsque les représentations des sommets et d’arêtes sont tous deux présents, on peut passer d’un graphe à l’autre. Il existe donc quatre mises à jour possibles (les sommets mettent à jour les sommets, les sommets mettent à jour les arêtes, les arêtes mettent à jour les sommets et les arêtes mettent à jour les arêtes), qui peuvent être alternées à volonté ou, moyennant des modifications mineures, les sommets peuvent être mis à jour simultanément à partir des sommets et des arêtes.
Implémentation#
On étudie ici la classification semi-supervisée des sommets d’un graphe sur un jeu de données classique (club de karaté de Zachary) . Ce jeu de données est un réseau d’amitiés entre 34 membres d’un club de karaté d’une université dans les années 1970. Une arête entre deux sommets indique que les deux membres ont interagi en dehors du club. Pendant que l’auteur collectait les données, un conflit est survenu entre le président du club (Mr. Hi) et l’entraîneur (Officer), ce qui a conduit à la division du club. Certains membres ont formé un nouveau club autour de l’entraîneur, tandis que d’autres ont trouvé un nouvel entraîneur ou ont abandonné le karaté. Au total, 4 sous-groupes ont été créés.
En utilisant uniquement les informations de connectivité (les arêtes), il est possible de retrouver ces sous-groupes.
On se pose donc la question suivante : Peut-on utiliser les GCN pour prédire l’affiliation de chaque membre étant donné les seules informations du président du club et de l’entraîneur ?
On utilise dans la suite la librairie PyG
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
from IPython.display import HTML
import networkx as nx
from torch_geometric.datasets import KarateClub
from torch_geometric.utils import to_dense_adj,to_networkx
from torch_geometric.nn import GCNConv
On récupère les données et on affiche les caractéristiques du réseau
dataset = KarateClub()
data = dataset[0]
print(f'Nombre de noeuds: {dataset.num_features}')
print(f'Nombre de classes: {dataset.num_classes}')
# Matrice d'adjacence
A = to_dense_adj(data.edge_index)[0].numpy().astype(int)
plt.imshow(A,cmap=plt.cm.gray)
plt.colorbar(ticks=[0, 1])
plt.title("Matrice d'adjacence")
Nombre de noeuds: 34
Nombre de classes: 4
Text(0.5, 1.0, "Matrice d'adjacence")
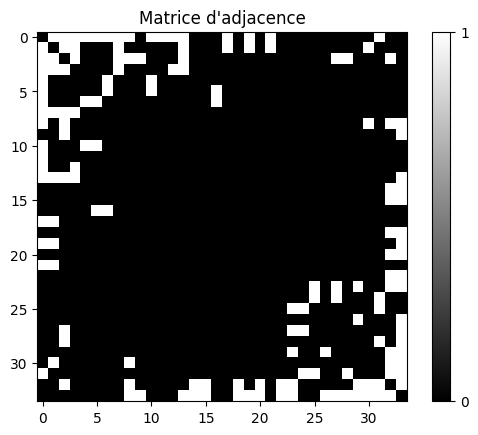
Dans les données initiales, le champ data.train_maskcontient un masque permettant de ne sélectionner dans les données qu’un membre de chaque classe
mask = data.train_mask
print(mask)
tensor([ True, False, False, False, True, False, False, False, True, False,
False, False, False, False, False, False, False, False, False, False,
False, False, False, False, True, False, False, False, False, False,
False, False, False, False])
On souhaite juste retrouver les groupes en fonction des données de l’entraîneur et du président. On modifie donc ce masque
mask[4]= False
mask[8]= False
mask[24]= False
mask[33]= True
print(mask)
tensor([ True, False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False, False,
False, False, False, True])
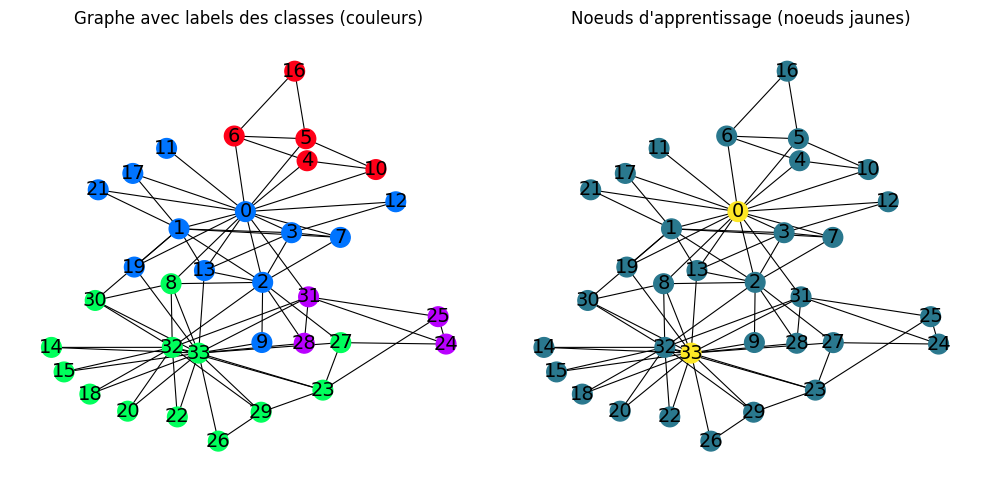
On affiche le graphe avec les groupes, et le graphe qui servira pour l’entraînement : seules les données des noeuds jaunes seront connues. On encode les informations des noeuds par un vecteur one hot encoder.
def oneHotEncoder(labels):
return np.sum([(labels[:, i] == 1) * (i + 1) for i in range(4)], axis=0)
np.random.seed(2)
G = to_networkx(data, to_undirected=True)
fig,axs = plt.subplots(1,2,figsize=(10,5))
plt.subplot(121)
plt.axis('off')
nx.draw_networkx(G,pos=nx.kamada_kawai_layout(G),with_labels=True,node_size=200,node_color=data.y,cmap="hsv",
vmin=-2,vmax=3,width=0.8,edge_color="black",font_size=14)
plt.title("Graphe avec labels des classes (couleurs)")
plt.subplot(122)
plt.axis('off')
nx.draw_networkx(G,pos=nx.kamada_kawai_layout(G),with_labels=True,node_size=200,node_color=oneHotEncoder(data.y * mask[:,np.newaxis]),
vmin=-2,vmax=3,width=0.8,edge_color="black",font_size=14)
plt.title("Noeuds d'apprentissage (noeuds jaunes)")
plt.tight_layout()
On construit ensuite un GCN simple
class GCN(torch.nn.Module):
def __init__(self):
super().__init__()
self.gcn = GCNConv(dataset.num_features, 3)
self.out = nn.Linear(3, dataset.num_classes)
def forward(self, x, edge_index):
h = self.gcn(x, edge_index).relu()
z = self.out(h)
return h, z
model = GCN()
et on apprend ce modèle
# Fonction de perte en classification
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.02)
def precision(pred_y, y):
return (pred_y == y).sum() / len(y)
pertes = []
precisions = []
res = []
nb_epochs = 70
for epoch in range(nb_epochs):
optimizer.zero_grad()
_, z = model(data.x, data.edge_index)
perte = criterion(z, data.y)
p = precision(z.argmax(dim=1), data.y)
perte.backward()
optimizer.step()
pertes.append(perte)
precisions.append(p)
res.append(z.argmax(dim=1))
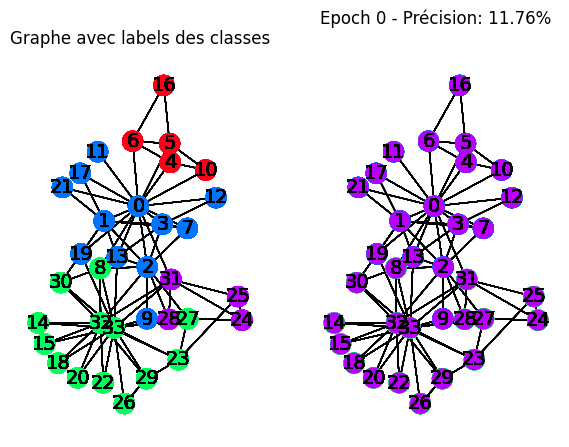
On affiche ensuite l’évolution de l’entraînement
plt.rcParams["animation.bitrate"] = 3000
def animate(i):
G = to_networkx(data, to_undirected=True)
plt.subplot(121)
plt.axis('off')
nx.draw_networkx(G,
pos=nx.kamada_kawai_layout(G),
with_labels=True,
node_size=200,
node_color=data.y,
cmap="hsv",
vmin=-2,
vmax=3,
width=0.8,
edge_color="black",
font_size=14
)
plt.title("Graphe avec labels des classes")
plt.subplot(122)
plt.axis('off')
nx.draw_networkx(G,pos=nx.kamada_kawai_layout(G, ),with_labels=True,node_size=200,
node_color=res[i],cmap="hsv",vmin=-2,vmax=3,width=0.8,edge_color="black",font_size=14)
plt.title(f'Epoch {i} - Précision: {precisions[i]*100:.2f}%', pad=20)
fig,axs = plt.subplots(1,2,figsize=(7,5))
anim = animation.FuncAnimation(fig, animate, np.arange(0, nb_epochs, 2), interval=500, repeat=True)
html = HTML(anim.to_html5_video())
from IPython.display import Video
Video("videos/gnn.mp4",embed =True,width=700)