Transformers#
Nous avons précédemment présenté les réseaux convolutifs, qui sont spécialisés dans le traitement des données qui se trouvent sur une grille régulière. Ils sont particulièrement adaptés au traitement des images, qui comportent un très grand nombre de variables d’entrée, ce qui exclut l’utilisation de réseaux entièrement connectés. Chaque couche d’un réseau convolutif utilise le partage des paramètres de manière à ce que les zones locales de l’image soient traitées de la même manière à chaque position dans l’image.
Nous introduisons ici les transformers, initialement destinés aux problèmes de traitement des langues naturelles, où l’entrée du réseau est une série d’encodages en grande dimension représentant des mots ou des fragments de mots. Les ensembles de données linguistiques partagent certaines des caractéristiques des données d’image. Le nombre de variables d’entrée peut être très important et les statistiques sont similaires à chaque position ; il n’est pas judicieux de réapprendre la signification du mot « maison » à chaque position possible dans un corps de texte. Cependant, les ensembles de données linguistiques présentent la complication suivante : les séquences de texte varient en longueur et, contrairement aux images, il n’existe pas de moyen facile de les redimensionner.
Motivation#
Pour motiver l’utilisation de transformers, considérons le texte suivant : « Le restaurant a refusé de me servir un sandwich au jambon parce qu’il ne cuisine que des plats végétariens. Finalement, ils m’ont donné deux tranches de pain. L’ambiance était tout aussi bonne que la nourriture et le service. »
L’objectif est de concevoir un réseau pour traiter ce texte dans une représentation adaptée aux tâches ultérieures. Par exemple, il pourrait être utilisé pour classer l’avis comme positif ou négatif ou pour répondre à des questions telles que « Le restaurant sert-il de la viande ? »
Trois observations immédiates peuvent être effectuées :
l’entrée codée peut être très grande. Dans ce cas, chacun des 41 mots pourrait être représenté par un vecteur de longueur 1024, de sorte que l’entrée codée serait de longueur 41\(\times\)1024=41984, même pour ce petit passage. Un corps de texte de taille plus réaliste peut comporter des centaines, voire des milliers de mots, de sorte que les réseaux complètement connectés ne sont pas utilisables en pratique.
l’une des caractéristiques des problèmes de reconnaissance automatique du langage est que chaque entrée (une ou plusieurs phrases) est de longueur différente ; il n’est donc même pas évident d’appliquer un réseau complètement connecté. Ces observations suggèrent que le réseau devrait partager des paramètres entre les mots à différentes positions d’entrée, de la même manière que les réseaux convolutifs partagent des paramètres entre différentes positions d’image.
le langage est ambigu : la syntaxe seule ne permet pas de savoir si le pronom « il » fait référence au restaurant ou au sandwich au jambon. Pour comprendre le texte, le mot « il » doit être relié d’une manière ou d’une autre au mot « restaurant ». Dans le langage des transformers, le premier mot doit prêter attention au second. Cela implique qu’il doit y avoir des liens entre les mots et que la force de ces liens dépend des mots eux-mêmes. En outre, ces liens doivent s’étendre sur de grandes parties du texte.
Mécanisme d’attention#
Mise en place#
Un modèle de traitement de texte (i) utilise le partage des paramètres pour traiter les longs passages d’entrée de différentes longueurs et (ii) contient des connexions entre les représentations de mots qui dépendent des mots eux-mêmes. Le transformer acquiert ces deux propriétés en utilisant un mécanisme d”(auto-)attention.
Une couche standard d’un réseau de neurones prend en entrée un vecteur \(\mathbf x\in\mathbb R^d\) et calcule une sortie du type
Un bloc d’attention \(A()\) prend \(N\) entrées \(\mathbf x_1,\cdots \mathbf x_N\) de \(\mathbb R^d\) et renvoie \(N\) vecteurs de sortie de la même taille. Dans le contexte du traitement automatique du langage, chaque entrée représente un mot ou un fragment de mot (token). Tout d’abord, un ensemble de vecteurs est calculé pour chaque entrée
Les poids et biais \(\mathbf W_v,\mathbf b_v\) sont les mêmes pour toutes les entrées. Puis les vecteurs de sortie sont calculés par
le scalaire \(a(\mathbf x_i,\mathbf x_j)\) étant l’attention que la \(j\)-ième sortie accorde à l’entrée \(x_i\). Les \(N\) valeurs \(a(\bullet ,\mathbf x_j)\) sont positifs et de somme unité.
Pour calculer l’attention, on définit deux transformations linéaires des entrées :
où les \(\mathbf q_i\) (respectivement \(\mathbf k_i\)) sont les requêtes (resp. clés). Ces dénominations proviennent de la théorie des bases de données.
Un produit scalaire entre requêtes et clés est alors effectué, et passé à un softmax (pour assurer la positivité et la somme à un)
Le produit scalaire entre requête et clé donne une mesure de similarité entre ces deux entités, et l’attention \(a(\bullet ,\mathbf x_j)\) dépend donc de la similarité entre \(q_j\) et toutes les clés.
Cette approche permet d’avoir un jeu de paramètres partagé entre toutes les entrées (\(\mathbf W_v,\mathbf b_v,\mathbf W_q,\mathbf b_q,\mathbf W_k,\mathbf b_k\)), indépendant de \(N\) et le réseau correspondant peut être appliqué à des entrées de longueur quelconque.
Formulation matricielle#
En formant la matrice \(\mathbf X\in\mathcal{M}_{d,N}(\mathbb R)\) dont les colonnes sont les \(\mathbf x_i\), alors le mécanisme d’attention (Fig. 52) peut s’écrire :
\(Softmax\) appliquant des fonctions softmax indépendantes sur chaque colonne de la matrice argument.
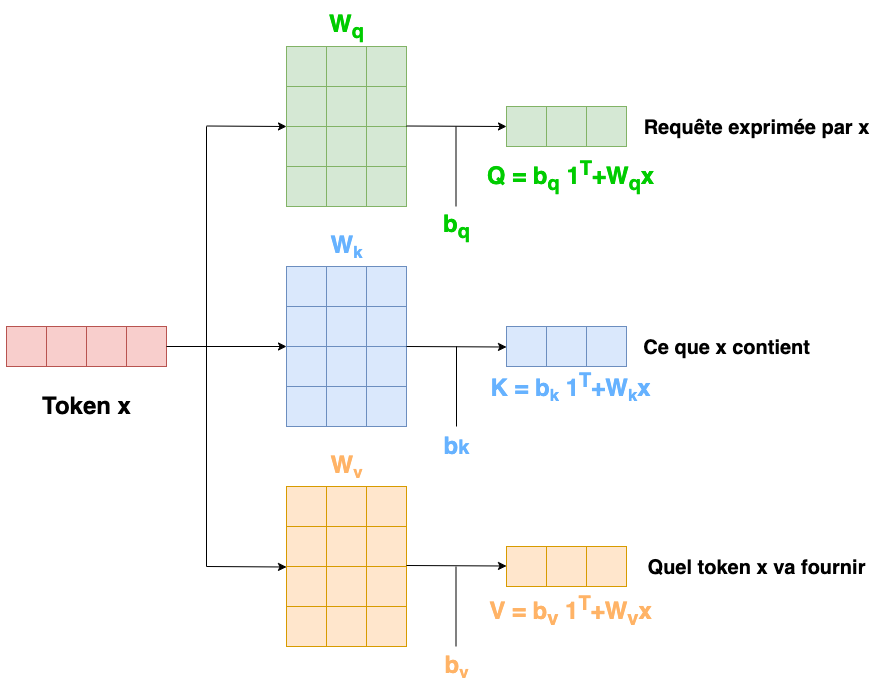
Fig. 52 Bloc d’attention#
Extensions#
Le mécanisme précédent, dit d’auto-attention (self attention) est décliné en plusieurs variantes très utilisées en pratique.
Encodage positionnel#
Le mécanisme d’auto-attention ne tient pas compte d’une information importante : le calcul est le même quel que soit l’ordre des entrées \(\mathbf x_i\). Plus précisément, il est équivariant par rapport aux permutations des entrées. Cependant, l’ordre est important lorsque les entrées correspondent aux mots d’une phrase. Il existe alors deux approches principales pour intégrer les informations de position :
l’encodage positionnel absolu : une matrice encodant l’information positionnelle \(\mathbf P\) est ajoutée aux entrées \(\mathbf X\). Chaque colonne de \(\mathbf P\) est unique et contient une information de position de l’entrée correspondante. \(\mathbf P\) peut être apprise ou fixée.
l’encodage positionnel relatif : l’entrée d’un mécanisme d’auto-attention peut être une phrase entière, plusieurs phrases ou un simple fragment de phrase, et la position absolue d’un mot est beaucoup moins importante que la position relative entre deux entrées. Si le système connaît la position absolue des deux entrées, la position relative peut être déterminée, mais les codages positionnels relatifs encodent directement cette information. Chaque élément de la matrice d’attention correspond à un décalage particulier entre la position de la requête et la position de la clé. Les codages positionnels relatifs apprennent un paramètre pour chaque décalage et l’utilisent pour modifier la matrice d’attention en ajoutant ces valeurs, en les multipliant ou en les utilisant pour modifier la matrice d’attention d’une autre manière.
Il existe de nombreuses raisons pour lesquelles un nombre unique, tel que l’indice de position, n’est pas utilisé en pratique. Par exemple, pour les longues séquences, ces indices peuvent devenir très importants. Même si on normalise ces indices entre 0 et 1, des problèmes persistent, notamment pour les séquences de longueur variable, qui seront normalisées différemment.
Chaque position est en fait encodée par un vecteur. Les auteurs de [1] proposent l’encodage suivant : pour une séquence (texte) de longueur \(L\) dans laquelle on recherche la position du \(k\)-ème token,\(k\in[\![0,L/2]\!]\), l’encodage est donné pour tout \(i\in[\![0,d/2]\!]\)par
avec \(n\) grand (égal à \(10^4\) dans [1]).
L’encodage des tokens et des positions est ensuite combiné, pour servir d’entrée au transformer (Fig. 53).
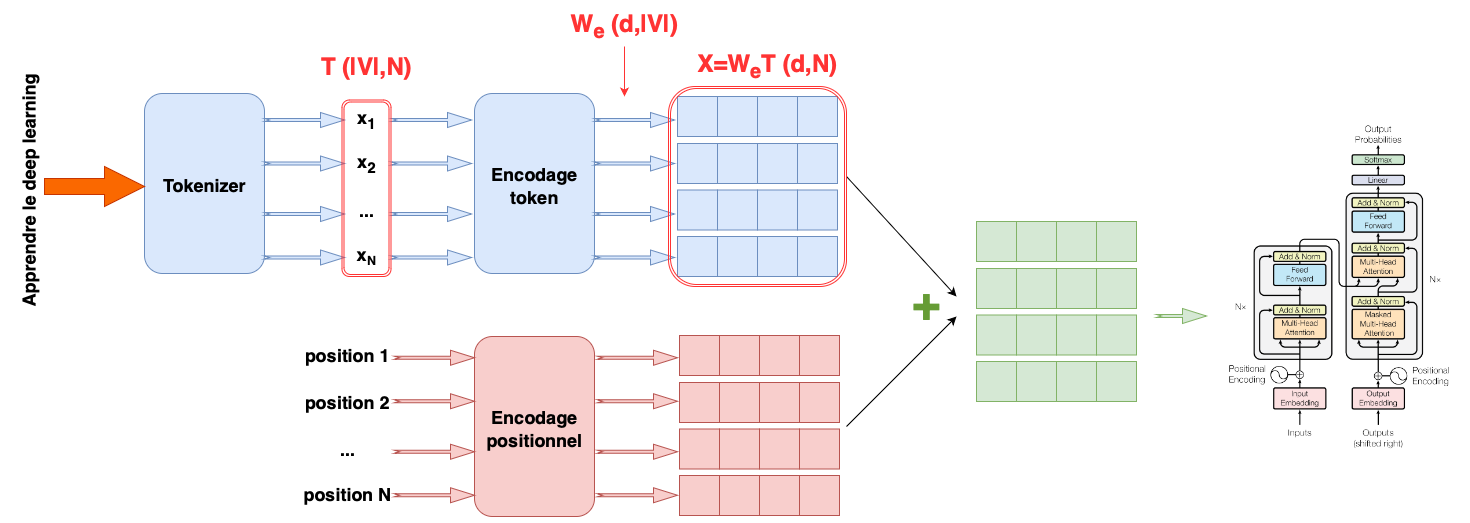
Fig. 53 Encodages de tokens et positionnel#
Une taille \(d\) typique est de 1024, et une taille totale de vocabulaire \(|V|\) typique est de 30 000, donc ce modèle nécessite de nombreux paramètres à apprendre, avant même la mise en place des transformers.
Auto attention par produit scalaire mis à l’échelle#
Les produits scalaires dans le calcul de l’attention peuvent avoir de grandes amplitudes et déplacer les arguments de la fonction softmax dans une région où la plus grande valeur domine. De petites modifications des entrées de la fonction softmax ont désormais peu d’effet sur la sortie (les gradients sont très faibles), ce qui rend le modèle difficile à entraîner. Pour éviter cet inconvénient, les produits scalaires sont mis à l’échelle par la racine carrée de la dimension \(d_q\) des requêtes et des clés :
Mécanisme d’auto attention multiple#
\(H\) ensembles de requêtes et clés sont calculés
\(\mathbf A_h(\mathbf X)\) est le \(h\)-ième mécanisme d’attention ou tête (head) (Fig. 54).
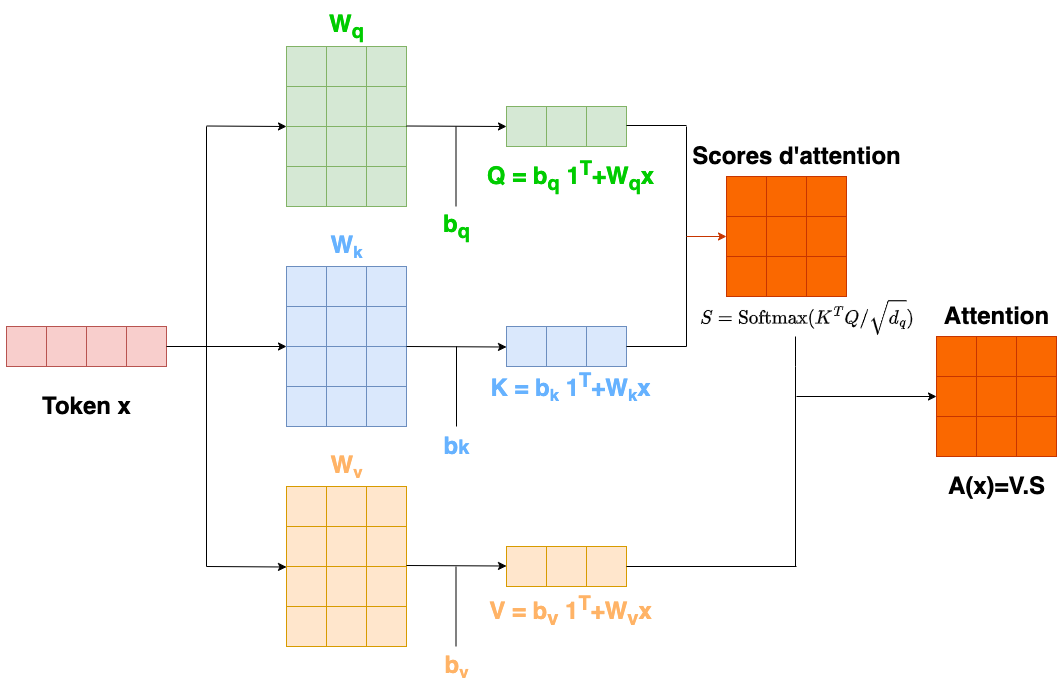
Fig. 54 Mécanisme d’attention#
Typiquement, si la dimension des entrées \(\mathbf x_i\) est \(d\) et qu’il y a \(H\) têtes, les valeurs, les requêtes et les clés seront toutes de taille \(d/H\) pour une implémentation efficiente. Les sorties de ces mécanismes d’auto-attention sont concaténées verticalement, et une autre transformation linéaire \(\mathbf W_c\) est appliquée pour les combiner
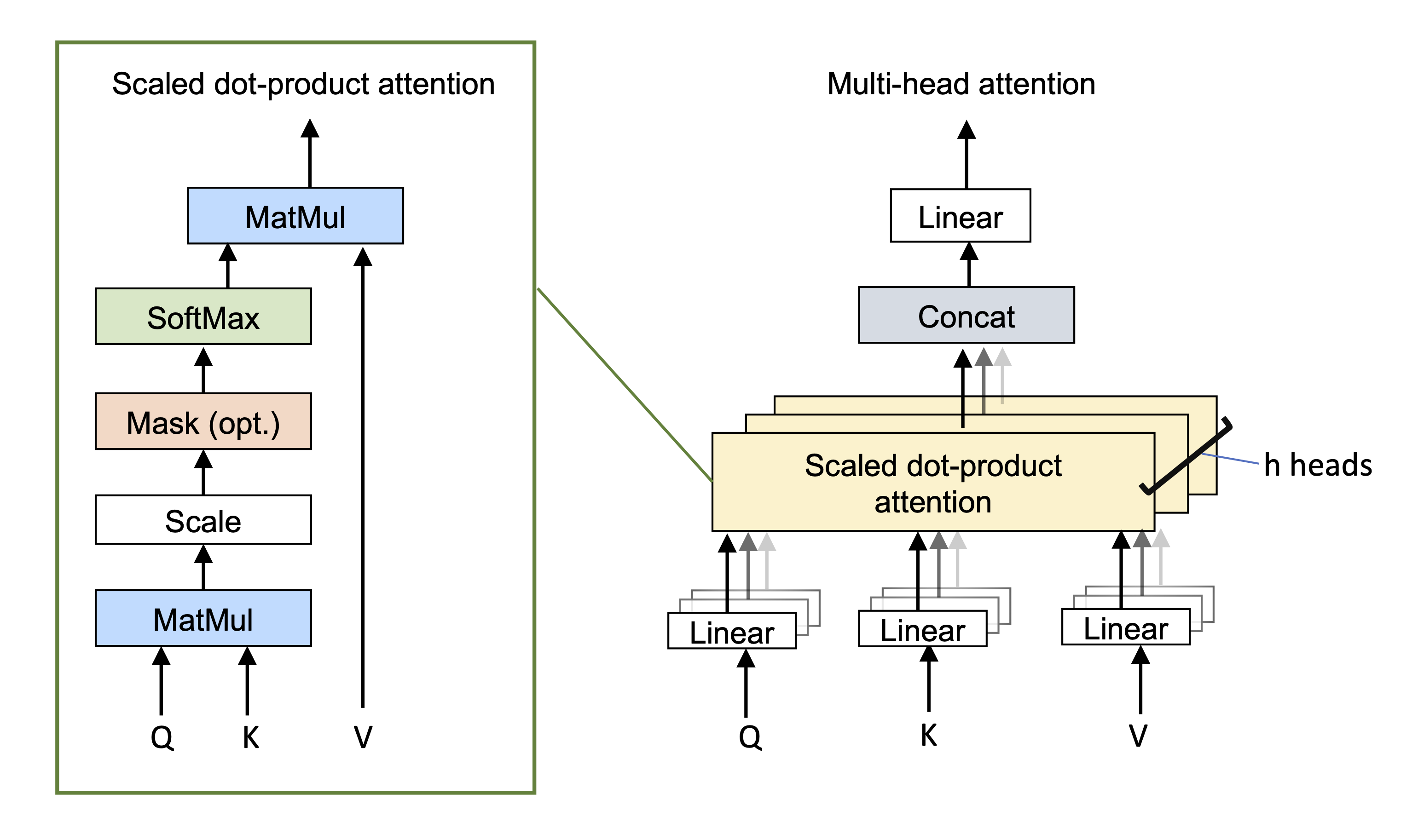
Fig. 55 Mécanisme d’auto attention multiple.#
Les têtes multiples semblent être nécessaires au bon fonctionnement du transformer, on pense qu’elles rendent le réseau d’auto-attention plus résistant aux mauvaises initialisations.
Transformers#
L’auto-attention n’est qu’une partie d’un mécanisme plus large : le bloc transformer (Fig. 56). Celui-ci se compose d’une unité d’auto-attention à plusieurs têtes (qui permet aux représentations de mots d’interagir les unes avec les autres) suivie d’un perceptron multicouches \(MLP\) qui opère séparément sur chaque mot. Les deux unités sont des réseaux résiduels (leur sortie est ajoutée à l’entrée d’origine). En outre, il est courant d’ajouter une opération de normalisation de couche \(LayerNorm\) après les réseaux d’auto-attention et les perceptrons multicouches. La séquence d’opérations complète peut être décrite par
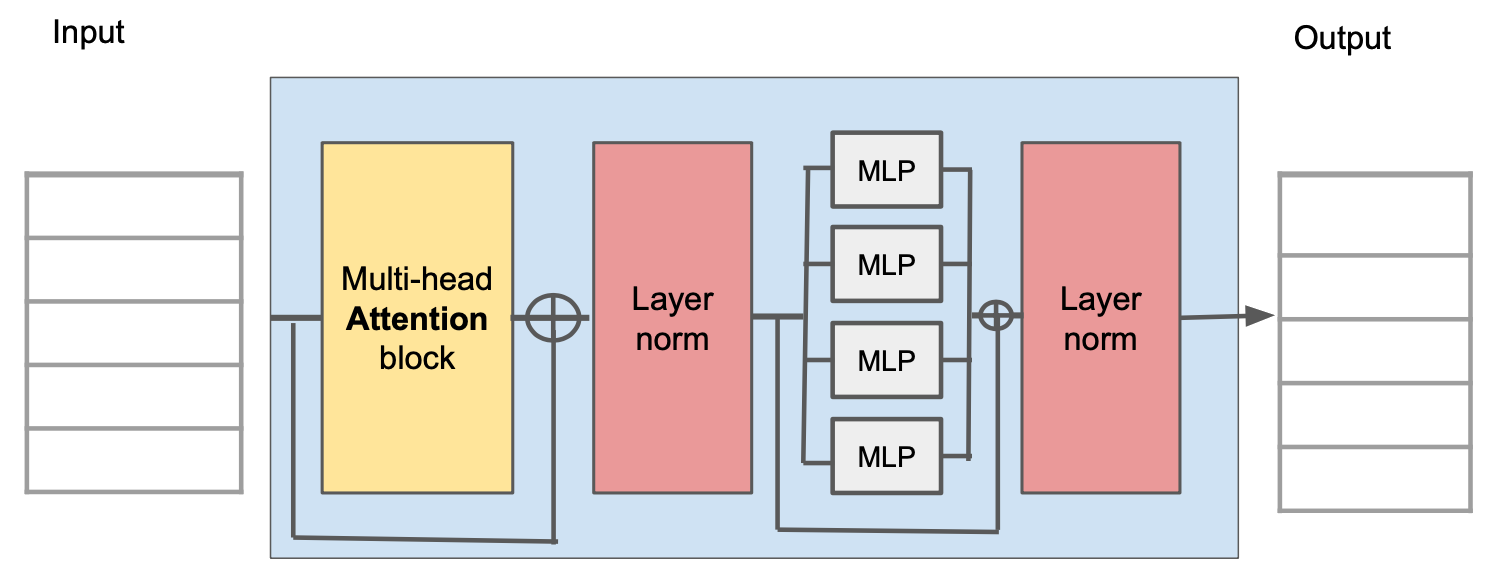
Fig. 56 Bloc transformer.#
En pratique, les données passent par plusieurs de ces blocs, qui composent le transformer.
Les transformers en traitement automatique du langage#
Une chaîne classique de traitement en classique en NLP commence par un tokenizer qui divise le texte en mots ou en fragments de mots. Chacun de ces tokens est ensuite mis en correspondance avec une représentation apprise. Ces représentations passent par une série de transformers.
Tokenizer#
Le texte est tout d’abord divisé en unités constitutives plus petites (jetons ou tokens) à partir d’un vocabulaire de jetons possibles. Ces jetons ne représentent pas nécessairement ces mots car :
inévitablement, certains mots (par exemple, des noms propres) ne figureront pas dans le vocabulaire.
la manière de gérer la ponctuation n’est pas claire, mais elle est importante. Si une phrase se termine par un point d’interrogation, il faut encoder cette information.
Le vocabulaire aurait besoin de différents jetons pour les versions d’un même mot avec des suffixes différents (par exemple, marche, marches, marché, marchés), et il n’y a aucun moyen de clarifier que ces variations sont liées.
Une approche consisterait à utiliser les lettres et les signes de ponctuation comme vocabulaire, mais cela impliquerait de découper le texte en très petites parties et d’exiger du réseau subséquent qu’il réapprenne les relations entre elles.
Dans la pratique, un compromis entre les lettres et les mots complets est utilisé, et le vocabulaire final comprend à la fois des mots courants et des fragments de mots à partir desquels des mots plus grands et moins fréquents peuvent être composés. Le vocabulaire est calculé à l’aide d’un tokeniser de sous-mots tel que le codage par paires d’octets, qui fusionne de manière gloutonne les sous-chaînes les plus courantes en fonction de leur fréquence.
Représentation#
Chaque jeton du vocabulaire \(V\) est associé à une représentation (embedding) de mot unique, et les représentations pour l’ensemble du vocabulaire sont stockées dans une matrice \(\mathbf W_e\in\mathcal{M}_{d,|V|}(\mathbb{R})\). Pour ce faire, les \(N\) jetons d’entrée sont d’abord encodés dans une matrice \(\mathbf T \in\mathcal{M}_{|V|,N}(\mathbb{R})\), où la \(n\)-ième colonne correspond au \(n\)-ième jeton et est un vecteur one-hot (un vecteur où chaque entrée est zéro, sauf l’entrée correspondant au jeton, de valeur 1). Les représentations des entrées sont calculées sous la forme \(\mathbf X =\mathbf W_e\mathbf T\) et \(\mathbf W_e\) est appris comme n’importe quel autre paramètre du réseau.
Ces encodages ne sont pas dépendant de la position des tokens dans le texte. On combine alors ces encodages par un encodage positionnel. L’encodage des tokens et des positions est ensuite combiné, pour servir d’entrée au transformer (Fig. 53).
Transformers#
Enfin, la matrice \(X\) représentant le texte passe par une série de \(K\) transformers.
Il existe trois types de ces modèles, brièvement décrits dans les paragraphes suivants. Globalement, un encodeur transforme la représentation du texte en une représentation qui peut prendre en charge une variété de tâches. Un décodeur prédit le prochain jeton pour poursuivre le texte d’entrée. Les encodeurs-décodeurs sont utilisés dans les tâches de séquence à séquence, où une chaîne de texte est convertie en une autre (par exemple, traduction automatique).
Exemple de modèle à encodeur : BERT#
BERT (Bidirectional Encoder Representations from Transformers) est un modèle d’encodeur qui utilise un vocabulaire de 30 000 mots. Les jetons d’entrée sont convertis en représentations de mots à 1024 dimensions et passent par \(K\)=24 transformers. Chacun d’eux contient un mécanisme d’auto-attention avec 16 têtes. Les requêtes, les clés et les valeurs de chaque tête sont de dimension 64. La dimension de la couche cachée unique dans le réseau complètement connecté du transformer est de 4096. Le nombre total de paramètres est de 340 millions. Lors de la publication de BERT, ce nombre était considéré comme élevé, mais il est aujourd’hui bien inférieur à celui des modèles les plus récents. Les modèles d’encodeurs comme BERT exploitent l’apprentissage par transfert. Pendant le préapprentissage, les paramètres de l’architecture du transformer sont appris par auto-supervision (pas besoin de labels) à partir d’un large corpus de texte. L’objectif est ici que le modèle apprenne des informations générales sur les statistiques de la langue. Au cours de la phase de fine tuning, le réseau résultant est adapté pour résoudre une tâche particulière à l’aide d’un plus petit corpus de données d’apprentissage supervisé.
Exemple de modèle à décodeur : GPT3#
On présente ici une description de haut niveau de GPT3. Le modèle sera développé ici L’architecture de base est très similaire à celle du modèle d’encodage et comprend une série de transformers qui opèrent sur les représentations de mots appris. Cependant, l’objectif est différent. L’encodeur vise à construire une représentation du texte qui peut être affinée pour résoudre une variété de tâches plus spécifiques. À l’inverse, le décodeur n’a qu’un seul objectif : générer le jeton suivant dans une séquence. Il peut générer un passage de texte cohérent en réinjectant la séquence étendue dans le modèle.
Modélisation du langage : GPT3 construit un modèle linguistique autorégressif. Pour illustrer ce modèle, considérons la phrase \(\mathcal{P}\) = « Henri mange beaucoup de viande le soir ». Pour simplifier, supposons que les jetons sont les mots complets. La probabilité de la phrase complète est :
Auto-attention masquée : pour entraîner un décodeur, on maximise la log-probabilité du texte d’entrée dans le cadre du modèle autorégressif. L’idéal serait de transmettre la phrase entière et de calculer simultanément toutes les log-probabilités et tous les gradients. Cependant, cela pose un problème : si on transmet la phrase complète, le terme qui calcule \(log P(\textrm{beaucoup}|\textrm{Henri mange})\) a accès à la fois à la réponse attendue « beaucoup » et au contexte suivant « de viande le soir ». Par conséquent, le système peut tricher au lieu d’apprendre à prédire les mots suivants et ne s’entraînera pas correctement. Fort heureusement, les jetons n’interagissent que dans les couches d’auto-attention d’un réseau transformer. Le problème peut donc être résolu en s’assurant que l’attention portée à la réponse et au contexte est nulle. Pour ce faire, les produits scalaires correspondants dans le calcul de l’auto-attention sont réglés à \(-\infty\) avant d’être passés à la fonction softmax. C’est le principe de l’auto-attention masquée. L’ensemble du réseau du décodeur fonctionne comme suit. Le texte d’entrée est encodé en jetons, et les jetons sont convertis en embeddings. Ces derniers sont transmis au réseau de transformers, qui utilisent l’auto-attention masquée, de sorte qu’ils ne peuvent s’intéresser qu’aux jetons actuels et précédents. Chacune des représentations de sortie peut être considérée comme représentant une phrase partielle, et pour chacune d’entre elles, l’objectif est de prédire le jeton suivant dans la séquence.
Après les transformers, une couche linéaire fait correspondre chaque représentation de mot à la taille du vocabulaire, suivie d’une fonction softmax qui convertit ces valeurs en probabilités. Pendant l’apprentissage, on cherche à maximiser la somme des log-probabilités de l’élément suivant dans la séquence de référence à chaque position en utilisant une fonction de perte d’entropie croisée multiclasse standard.
Génération de texte : puisque ce modèle définit un modèle de probabilité sur des séquences de texte, il peut être utilisé pour échantillonner de nouveaux exemples de texte plausibles. Pour générer à partir du modèle, on débute par une séquence de texte en entrée (qui peut être simplement un jeton spécial \(<\)start\(>\) indiquant le début de la séquence) et on l’introduit dans le réseau, qui produit alors les probabilités sur les jetons suivants possibles. On peut alors choisir le jeton le plus probable ou échantillonner à partir de la distribution de probabilités construite. La nouvelle séquence étendue peut être réinjectée dans le réseau du décodeur qui fournit la distribution de probabilités sur le jeton suivant. En répétant ce processus, on génère un texte entier.
En pratique, de nombreuses stratégies peuvent rendre le texte de sortie plus cohérent. Par exemple, la recherche par faisceau tient compte des nombreux compléments de phrases possibles pour trouver le plus probable (qui n’est pas nécessairement trouvé en choisissant de manière gloutonne le mot suivant le plus probable à chaque étape). L’échantillonnage top-k tire aléatoirement le mot suivant parmi les \(k\) possibilités les plus probables afin d’éviter que le système ne choisisse accidentellement dans la longue traîne des jetons à faible probabilité, ce qui conduirait à une impasse linguistique.
GPT3 est un exemple de LLM (Large Language Model). La longueur des séquences est de 2048 jetons. Il y a \(K\)=96 transformers, chacun calculant une représentation de taille 12288. Dans les couches d’auto attention, on compte 96 têtes et la dimension des requêtes et des clés est de 128. Tout celà amène à un nombre de paramètres de 175 milliards, entraînés sur 300 milliards de jetons (taille d’un batch : 3.2 million de jetons)
Exemple de modèle à encodeur-décodeur : traduction automatique#
La traduction entre langues est un exemple de tâche de séquence à séquence. Cette tâche nécessite un encodeur (pour calculer une bonne représentation de la phrase source) et un décodeur (pour générer la phrase dans la langue cible). Cette tâche peut être abordée à l’aide d’un modèle encodeur-décodeur. Prenons l’exemple d’une traduction de l’anglais vers le français. L’encodeur reçoit la phrase en anglais et la traite à travers une série de transformers pour créer une représentation de sortie pour chaque jeton. Pendant l’entraînement, le décodeur reçoit la traduction de référence en français et la fait passer par une série de transformers qui utilisent l’auto-attention masquée et prédisent le mot suivant à chaque position.
Cependant, les couches du décodeur s’occupent également de la sortie de l’encodeur. Par conséquent, chaque mot français en sortie est conditionné par les mots précédents en sortie et par l’ensemble de la phrase anglaise qu’il traduit. Pour ce faire, on modifie les transformers du décodeur. Le transformer original du décodeur consistait en une couche d’auto-attention masquée suivie d’un réseau appliqué individuellement à chaque représentation. Une nouvelle couche d’auto-attention est alors ajoutée entre ces deux composants, dans laquelle les représentations du décodeur s’intéressent aux représentations de l’encodeur. Cette méthode utilise une version de l’auto-attention connue sous le nom d’attention encodeur-décodeur ou d’attention croisée, où les requêtes sont calculées à partir des représentations du décodeur et les clés et valeurs à partir des représentations de l’encodeur.
Les transformers en traitement d’images#
Le succès des transformers en traitement automatique du langage a conduit à se pencher sur leur utilisation sur des images. L’idée semblait incongrue, et ce pour deux raisons : il y a beaucoup plus de pixels dans une image que de mots dans une phrase, de sorte que la complexité quadratique de l’auto-attention constitue un goulot d’étranglement pratique. De plus, les réseaux convolutifs ont un bon biais inductif parce que chaque couche est équivariante à la translation spatiale et qu’ils prennent en compte la structure 2D de l’image. Ce qu’il faudrait apprendre dans un réseau transformer. Malgré cela, les réseaux transformers ont désormais éclipsé les performances des réseaux convolutifs pour entre autres la classification d’images. Cela s’explique en partie par l’échelle à laquelle ils peuvent être construits et par les grandes quantités de données qui peuvent être utilisées pour pré-entraîner les réseaux.
ImageGPT#
ImageGPT est un décodeur. Il construit un modèle autorégressif de pixels qui assimile une image partielle et prédit la valeur du pixel suivant. La complexité quadratique du réseau de transformers signifie que le plus grand modèle (qui contient 6,8 milliards de paramètres) ne peut fonctionner que sur des images de taille 64\(\times\)64. En outre, pour que le système soit viable, l’espace colorimétrique RVB original de 24 bits a dû originellement être quantifié en un espace colorimétrique de neuf bits, de sorte que le système assimile (et prédit) l’un des 512 jetons possibles à chaque position. Les images sont naturellement des objets 2D, mais ImageGPT apprend simplement un codage positionnel différent pour chaque pixel. Il doit donc apprendre que chaque pixel a une relation étroite avec ses voisins précédents ainsi qu’avec les pixels voisins de la rangée supérieure.
La représentation interne de ce décodeur a été utilisée comme base pour la classification des images. Les représentations finales des pixels sont moyennées et une couche linéaire les met en correspondance avec des activations qui passent par une couche softmax pour prédire les probabilités de classe. Le système est pré-entraîné sur un large corpus d’images web, puis affiné sur la base de données ImageNet redimensionnée à 48\(\times\)48 pixels à l’aide d’une fonction de perte qui contient à la fois un terme d’entropie croisée pour la classification des images et un terme de perte générative pour la prédiction des pixels. Malgré l’utilisation d’une grande quantité de données d’apprentissage externes, le système a obtenu un taux d’erreur de 27,4% sur ImageNet. Ce taux est inférieur à celui des architectures convolutives de l’époque, mais reste impressionnant compte tenu de la petite taille de l’image d’entrée ; sans surprise, il ne parvient pas à classer les images où l’objet cible est petit ou mince.
ViT : Vision Transformer#
ViT s’est attaqué au problème de la résolution de l’image en divisant l’image en patchs de 16\(\times\)16 . Chaque patch est mis en correspondance avec une dimension inférieure par le biais d’une transformation linéaire apprise, et ces représentations sont introduites dans le réseau du transformer. Les codages positionnels 1D standard sont appris. Il s’agit d’un modèle encodeur avec un jeton \(<\)cls\(>\). Cependant, contrairement à BERT, il utilise un pré-entraînement supervisé sur une grande base de données de 303 millions d’images étiquetées provenant de 18 000 classes. Le jeton \(<\)cls\(>\) est mappé via une couche finale du réseau pour créer des activations qui sont introduites dans une fonction softmax pour générer des probabilités de classe.
Après le pré-entraînement, le système est appliqué en classification en remplaçant la couche finale par une couche qui correspond au nombre de classes souhaité et qui est ajustée par fine tuning. Ce système a obtenu un taux d’erreur de 11,45% pour le top 1 sur ImageNet. Cependant, il n’a pas obtenu d’aussi bons résultats que les meilleurs réseaux convolutifs contemporains sans pré-entraînement supervisé. Le fort biais inductif des réseaux convolutifs ne peut être surmonté que que par l’utilisation de quantités extrêmement importantes de données d’entraînement.
Implémentation#
Vu les temps d’entraînement et les bases de données nécessaires, il est impossible de proposer de faire tourner un transformer sans beaucoup de ressources. On se propose donc ici d’implémenter un Transformer de bout en bout, et plus particulièrement le travail séminal sur ce sujet [1]. Dans la mesure du possible, on propose en illustration des codes les figures de l’article.
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
import numpy as np
On implémente le mécanisme d’auto-attention multiple (multihead attention)
class MultiHeadAttention(nn.Module):
def __init__(self, d, H):
super(MultiHeadAttention, self).__init__()
assert d % H == 0,
self.d = d
self.H = H
self.d_q = d // H
self.W_q = nn.Linear(d, d)
self.W_k = nn.Linear(d, d)
self.W_v = nn.Linear(d, d)
self.W_o = nn.Linear(d, d)
# Calcul des attentions
def Ah(self, Q, K, V, mask=None):
attn_scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_q)
# Cas de l'auto-attention masquée
if mask is not None:
attn_scores = attn_scores.masked_fill(mask == 0, -1e10)
attn_probs = torch.softmax(attn_scores, dim=-1)
output = torch.matmul(attn_probs, V)
return output
# Redimensionne le tenseur d'entrée pour les têtes
def tetes(self, x):
batch_size, N, d = x.size()
return x.view(batch_size, N, self.H, self.d_q).transpose(1, 2)
# Combine les attentions de toutes les têtes
def concateneAttention(self, x):
batch_size, _, N, d_q = x.size()
return x.transpose(1, 2).contiguous().view(batch_size, N, self.d)
# Calcul l'auto-attention multiple.
def forward(self, Q, K, V, mask=None):
Q = self.tetes(self.W_q(Q))
K = self.tetes(self.W_k(K))
V = self.tetes(self.W_v(V))
attn_output = self.Ah(Q, K, V, mask)
output = self.W_o(self.concateneAttention(attn_output))
return output
On s’intéresse ensuite au codage positionnel des mots. On encode la position d’un mot à l’aide des formules proposées dans [1]. Pour ce faire, on créé une classe PositionFFN qui permet de prendre en compte la position des éléments dans le calcul des prédictions.
class PositionFFN(nn.Module):
def __init__(self, d, d_ff):
super(PositionFFN, self).__init__()
self.fc1 = nn.Linear(d, d_ff)
self.fc2 = nn.Linear(d_ff, d)
self.relu = nn.ReLU()
def forward(self, x):
return self.fc2(self.relu(self.fc1(x)))
Cette classe est ensuite utilisée dans l’encodage positionnel à proprement parler. On initialise un tenseur de taille \(d\times max\_N\) permettant de stocker les valeurs d’encodage.
class PositionalEncoding(nn.Module):
def __init__(self, d, max_N):
super(PositionalEncoding, self).__init__()
# Codage de l'encodage proposé dans l'article
pe = torch.zeros(max_N, d)
p = torch.arange(0, max_N, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d, 2).float() * -(math.log(10000.0) / d))
pe[:, 0::2] = torch.sin(p * div_term)
pe[:, 1::2] = torch.cos(p * div_term)
self.register_buffer('pe', pe.unsqueeze(0))
def forward(self, x):
return x + self.pe[:, :x.size(1)]
On construit ensuite l’encodeur (Fig. 57) et le décodeur (Fig. 58).
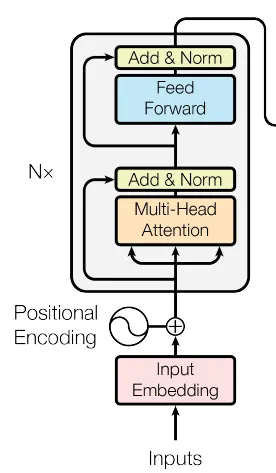
class EncoderLayer(nn.Module):
def __init__(self, d, H, d_ff, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = MultiHeadAttention(d, H)
self.feed_forward = PositionFFN(d, d_ff)
self.norm1 = nn.LayerNorm(d)
self.norm2 = nn.LayerNorm(d)
self.dropout = nn.Dropout(dropout)
def forward(self, x, mask):
attn_output = self.self_attn(x, x, x, mask)
# connexion résiduelle
x = self.norm1(x + self.dropout(attn_output))
ff_output = self.feed_forward(x)
# connexion résiduelle
x = self.norm2(x + self.dropout(ff_output))
return x
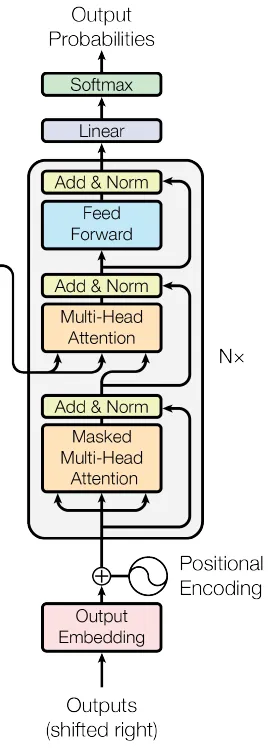
class DecoderLayer(nn.Module):
def __init__(self, d, H, d_ff, dropout):
super(DecoderLayer, self).__init__()
self.self_attn = MultiHeadAttention(d, H)
self.cross_attn = MultiHeadAttention(d, H)
self.feed_forward = PositionFFN(d, d_ff)
self.norm1 = nn.LayerNorm(d)
self.norm2 = nn.LayerNorm(d)
self.norm3 = nn.LayerNorm(d)
self.dropout = nn.Dropout(dropout)
def forward(self, x, enc_output, src_mask, tgt_mask):
attn_output = self.self_attn(x, x, x, tgt_mask)
x = self.norm1(x + self.dropout(attn_output))
attn_output = self.cross_attn(x, enc_output, enc_output, src_mask)
x = self.norm2(x + self.dropout(attn_output))
ff_output = self.feed_forward(x)
x = self.norm3(x + self.dropout(ff_output))
return x
et on assemble le tout en un bloc transformer (Fig. 59)
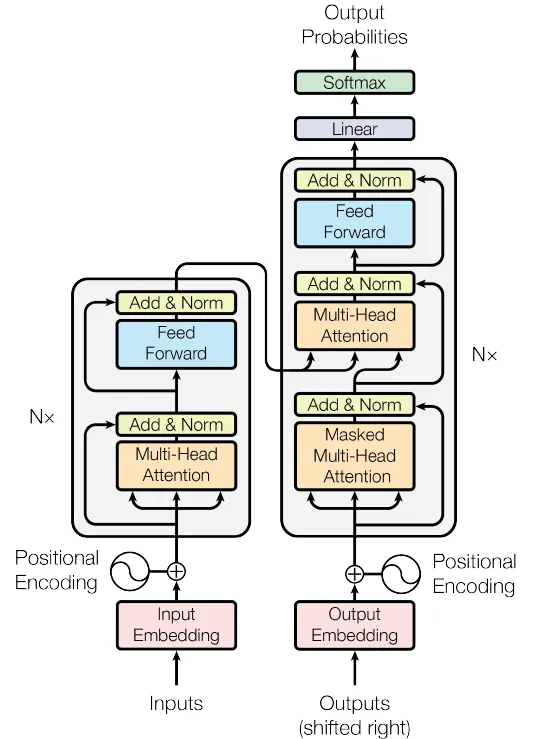
class Transformer(nn.Module):
def __init__(self, taille_voc_source, taille_voc_cible, d, H, nb_layers, d_ff, max_N, dropout):
super(Transformer, self).__init__()
self.encoder_embedding = nn.Embedding(taille_voc_source, d)
self.decoder_embedding = nn.Embedding(taille_voc_cible, d)
self.positional_encoding = PositionalEncoding(d, max_N)
self.encoder_layers = nn.ModuleList([EncoderLayer(d, H, d_ff, dropout) for _ in range(nb_layers)])
self.decoder_layers = nn.ModuleList([DecoderLayer(d, H, d_ff, dropout) for _ in range(nb_layers)])
self.fc = nn.Linear(d, taille_voc_cible)
self.dropout = nn.Dropout(dropout)
def generate_mask(self, src, cible):
src_mask = (src != 0).unsqueeze(1).unsqueeze(2)
cible_mask = (cible != 0).unsqueeze(1).unsqueeze(3)
N = cible.size(1)
nopeak_mask = (1 - torch.triu(torch.ones(1, N, N), diagonal=1)).bool()
cible_mask = cible_mask & nopeak_mask
return src_mask, cible_mask
def forward(self, src, cible):
src_mask, cible_mask = self.generate_mask(src, cible)
src_embedded = self.dropout(self.positional_encoding(self.encoder_embedding(src)))
cible_embedded = self.dropout(self.positional_encoding(self.decoder_embedding(cible)))
enc_output = src_embedded
for enc_layer in self.encoder_layers:
enc_output = enc_layer(enc_output, src_mask)
dec_output = cible_embedded
for dec_layer in self.decoder_layers:
dec_output = dec_layer(dec_output, enc_output, src_mask, cible_mask)
output = self.fc(dec_output)
return output
On peut alors tester ce transformer sur un jeu de données (ici simple et de synthèse)
taille_voc_source = 5000
taille_voc_cible = 5000
d = 512
H = 8
nb_layers = 6
d_ff = 2048
max_N = 100
dropout = 0.1
bath_size = 64
transformer = Transformer(taille_voc_source, taille_voc_cible, d, H, nb_layers, d_ff, max_N, dropout)
# Calcul du nombre de paramètres entraînables
model_parameters = filter(lambda p: p.requires_grad, transformer.parameters())
params = sum([np.prod(p.size()) for p in model_parameters])
print(params)
# Génération de deux séquences
src_data = torch.randint(1, taille_voc_source, (batch_size, max_N))
cible_data = torch.randint(1, taille_voc_cible, (batch_size, max_N))
criterion = nn.CrossEntropyLoss(ignore_index=0)
optimizer = optim.Adam(transformer.parameters(), lr=0.0001, betas=(0.9, 0.98), eps=1e-9)
l = []
transformer.train()
nb_epochs = 100
for epoch in range(nb_epochs):
optimizer.zero_grad()
output = transformer(src_data, cible_data[:, :-1])
loss = criterion(output.contiguous().view(-1, taille_voc_cible), cible_data[:, 1:].contiguous().view(-1))
loss.backward()
optimizer.step()
l.append(loss.item())
print(f"Epoch: {epoch+1}, Loss: {loss.item()}")
plt.plot(np.arange(nb_epochs),l)
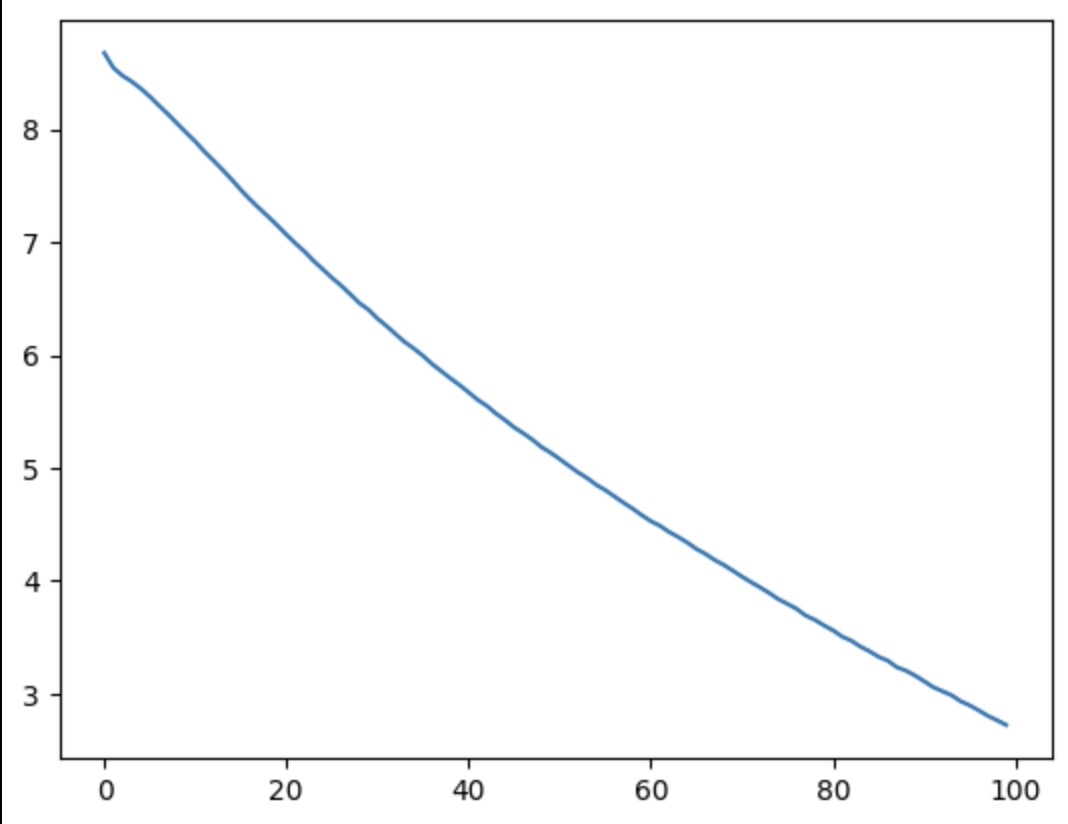
Fig. 60 Fonction de perte.#
src = torch.tensor([[0, 2, 5, 6, 4, 3, 9, 5, 2, 9, 10, 1]])
trg = torch.tensor([[0]])
print(src.shape,trg.shape)
out = transformer.forward(src, trg)
out
Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Ł ukasz Kaiser, and Illia Polosukhin. Attention is all you need. In I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc., 2017. URL: https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf.