Réseaux récurrents#
Définition#
Les réseaux de neurones récurrents (RNN, Recurrent Neural Networks) sont des réseaux à propagation avant, permettant de prendre en compte le temps. Comme dans les réseaux classiques, il n’existe pas de cycle, mais les arcs ajoutés pour introduire la notion de temps (les arcs récurrents) peuvent en revanche former des cycles, y compris de longueur 1 (connexion d’un neurone avec lui-même). À l’instant \(t\), les neurones possédant des arcs récurrents reçoivent en entrée la donnée courante \(\mathbf{x_t}\) et les valeurs des neurones cachés \({h_{t-1}}\) informant sur l’état précédent du réseau. La sortie \(\hat{y}_{t}\) est calculée étant donné l’état \(\mathbf{x_t}\) des neurones cachés à l’instant \(t\). La donnée \(\mathbf{x_{t-1}}\) peut influencer \(\hat{y}_{t}\) et la sortie aux instants suivants, à l’aide des arcs récurrents.
Deux équations permettent de calculer les quantités nécessaires à l’instant \(t\) dans la phase de propagation avant d’un réseau récurrent simple (comme celui de la Fig. 28 gauche) :
où \(\mathbf{W_{hx}}\) est la matrice des poids reliant
l’entrée à la couche cachée et \(\mathbf{W_{hh}}\) celle des poids des
arcs récurrents. Les biais sont notés \(b_h\) et \(b_y\).
La dynamique du réseau peut être décrite en dépliant ce réseau dans le
temps (Fig. 28 droite). Le réseau devient donc un réseau profond, avec une couche par instant \(t\) et un partage de poids au cours du temps. Ce dernier peut
donc être entraîné de manière classique par l’algorithme de
rétropropagation du gradient, indicé par le temps (Backpropagation
through time, BPTT algorithm).
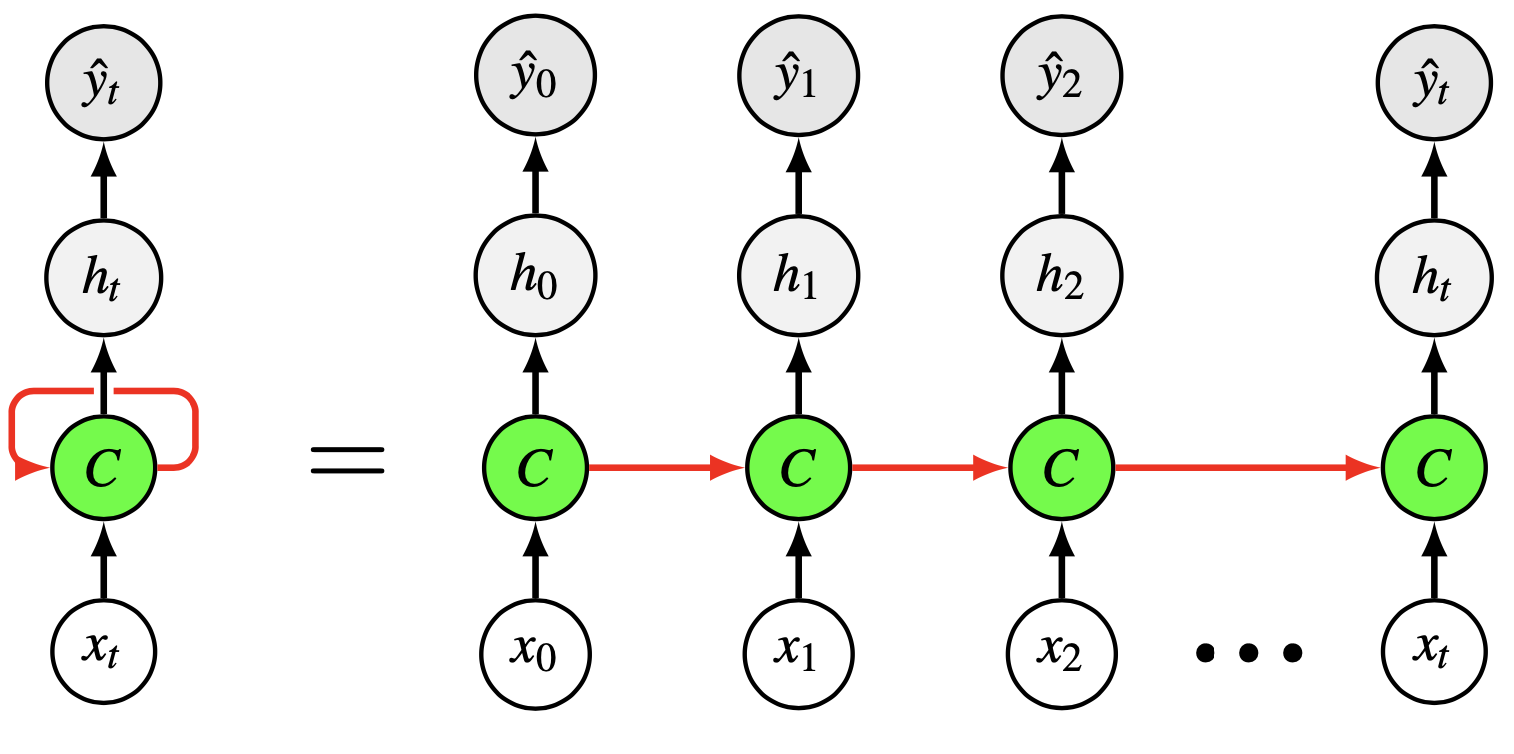
Fig. 28 Réseau récurrent et sa version dépliée dans le temps.#
Avec ces réseaux, il est possible de traiter des séquences de longueur quelconque, la taille du modèle étant indépendante de cette longueur. Plusieurs architectures peuvent être déclinées sur ce principe
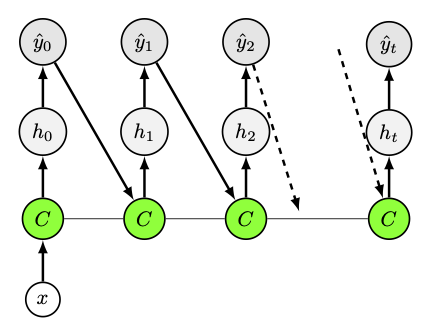
Fig. 29 Architectures « un vers plusieurs » , utilisées par exemple en génération de musique ou légendage d’images.#
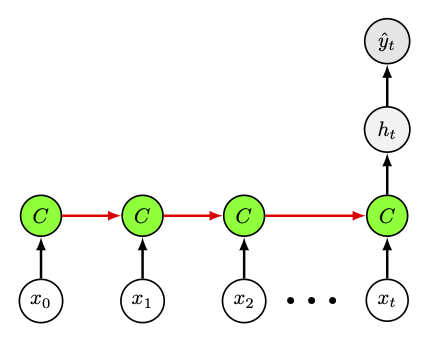
Fig. 30 Architectures « un vers plusieurs » , utilisées par exemple en classification de sentiments#
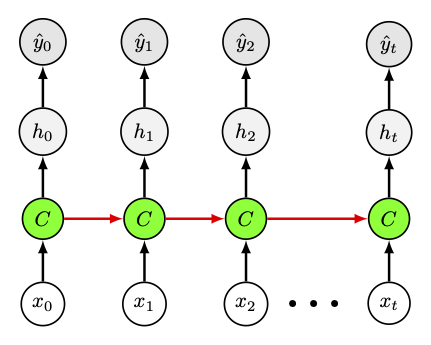
Fig. 31 Architectures « plusieurs vers plusieurs », pour la reconnaissance d’entité dans des textes ou annotation de vidéos.#
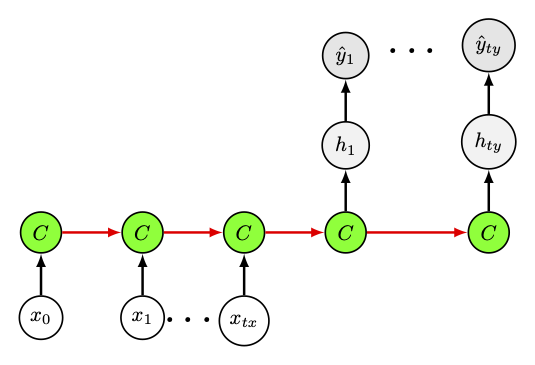
Fig. 32 Architectures « plusieurs vers plusieurs », pour la traduction automatique.#
Entraînement des réseaux récurrents#
L’apprentissage de dépendances long terme peut être difficile. Les problèmes d’évanescence (vanishing) ou d’explosion du gradient peuvent rapidement survenir, lors de la rétropropagation sur plusieurs pas de temps.
Prenons un exemple simple pour comprendre : considérons un réseau à un neurone d’entrée, un neurone récurrent caché et un neurone de sortie. On donne au réseau une entrée à l’instant \(t_0\) et on calcule l’erreur à l’instant \(t>t_0\), en supposant des entrées nulles entre \(t_0\) et \(t\). Le lien entre les poids au cours du temps fait que le poids sur l’arc récurrent ne change jamais. La contribution de l’entrée au temps \(t_0\) à la sortie au temps \(t\) deviendra de plus en plus importante, ou se rapprochera de zéro, de manière exponentielle à mesure que \(t-t_0\) croît. Et la dérivée de l’erreur par rapport à l’entrée explosera ou disparaîtra, selon que le poids de l’arc récurrent a une valeur absolue plus grande ou plus petite que 1 et selon la fonction d’activation du neurone caché (le problème du gradient évanescent est très présent avec une sigmoïde et une activation ReLU force davantage l’explosion).
Plusieurs solutions ont été proposées (régularisation, retropropagation tronquée, conception d’architecture et heuristiques) pour résoudre ces problèmes.
Quelques architectures#
LSTM#
Les réseaux Long Short-Term Memory (LSTM) ont été introduits en 1997 [1] pour résoudre le problème de l’évanescence du gradient. Ce modèle ressemble à un réseau récurrent classique à une couche cachée, mais chaque neurone de la couche cachée est remplacé par une cellule de mémoire.
Dans la suite, on note \(\mathbf{x_t}\) l’entrée de la cellule à l’instant \(t\), \({h_{t-1}}\) la sortie de la couche cachée calculée au temps \(t-1\). Au lieu de calculer une sortie du type \(\sigma\left( \mathbf{W^\top x}+b\right)\), la cellule contient plusieurs éléments distincts aux fonctions particulières. Les LSTM introduisent la notion de portes, qui sont des unités d’activation de type sigmoïde qui prennent comme arguments \(\mathbf{x_t}\) et \({h_{t-1}}\) et viennent pondérer des valeurs calculées dans la cellule. En particulier, si la valeur d’une porte est nulle, alors le flot est coupé dans le graphe, alors qu’il transite intégralement si la valeur de la porte est égale à 1.
On retrouve dans une cellule (Fig. 33) les éléments suivants :
Neurone d’entrée : ce neurone prend en entrée \(\mathbf{x_t}\) et \({h_{t-1}}\) et calcule, à la manière d’un neurone classique, une sortie \(g^{t} = \sigma\left(\mathbf{W_C^\top} \left[\mathbf{x_t}, {h_{t-1}}\right ] +b_C\right)\).
Porte d’entrée (ou de mise à jour) : la porte calcule \(i^{t} = \sigma\left(\mathbf{W_i}^\top \left[\mathbf{x_t}, {h_{t-1}}\right ] +b_i\right)\) et vient pondérer la valeur du neurone d’entrée pour décider de l’importance à lui donner au temps \(t\).
Porte d’oubli : cette porte calcule \(f^{t}=\sigma\left(\mathbf{W_f}^\top\left[\mathbf{x_t} , {h_{t-1}}\right ] +b_f\right)\) et permet au réseau d’oublier son état interne.
État interne : le cœur de la cellule de mémoire est son état interne, noté \(C^{t}\), composé d’un neurone récurrent à poids fixe unité, assurant que le gradient peut passer par cet arc de nombreuses fois sans disparaître ou exploser. La mise à jour de l’état interne est effectuée par une opération du type \(C^{t} =g^{t}.i^{t} + C^{(t-1)}.f^{t}\).
Porte de sortie : la valeur \(h_t\) produite par la cellule de mémoire est calculée comme le produit de \(tanh(C^{t})\) par la valeur de la porte de sortie \(o^{t}\). Cette porte sélectionne la part de \(C^{t}\) à fournir en sortie et est calculée par \(o^{t} = \sigma\left(\mathbf{W_o}^\top\left[\mathbf{x_t} , h_{t-1}\right ] +b_o\right)\).
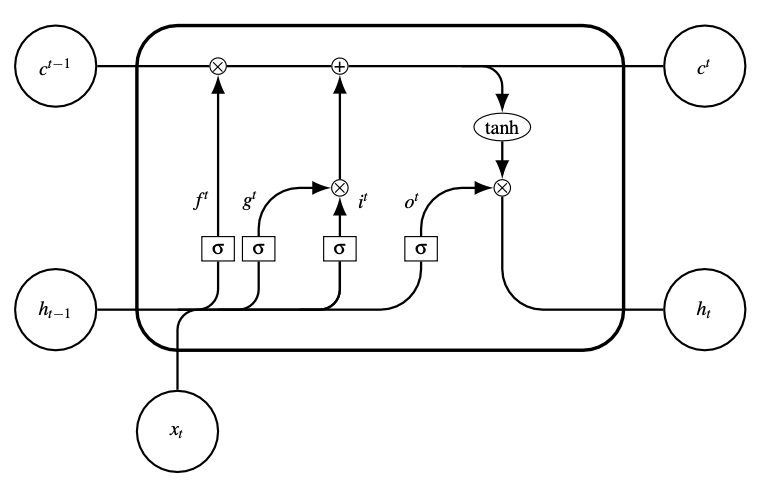
Fig. 33 Cellule LSTM#
En résumé, un LSTM effectue donc les opérations suivantes à l’instant \(t\) :
GRU#
En 2014 [2], une version simplifiée des réseaux LSTM a été introduite, qui nécessite moins de paramètres. Les GRU (Gated Recurrent Units) (Fig. 34) sont en effet des réseaux sans mémoire interne \(C^{t}\), ni porte de sortie \(o^{t}\). Ces réseaux sont composés de deux portes au lieu de trois :
une porte reset \(r^{t}\), qui détermine la manière de combiner la nouvelle entrée au temps \(t\) avec la mémoire provenant du temps \(t-1\).
une porte de mise à jour \(z^{t}\), qui détermine la quantité de mémoire précédente qui doit être conservée. Cette porte est la combinaison des portes d’entrée et d’oubli des LSTM.
Formellement :
Si, pour tout \(t, r^{t}=1\) et \(z^{t}=0\), alors on modélise un réseau récurrent classique.
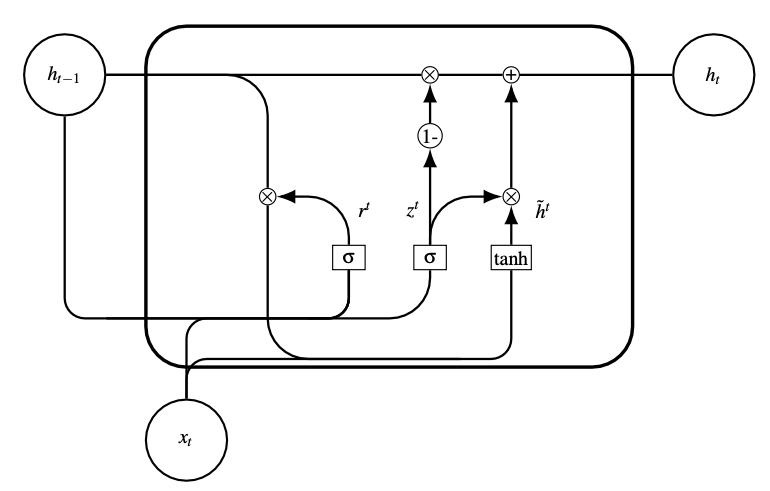
Fig. 34 Cellule GRU#
Réseaux récurrents bidirectionnels#
Les réseaux bidirectionnels ont été décrits pour la première fois en 1997 [3]. Dans ces réseaux, deux couches cachées sont présentes, chacune connectée à l’entrée et la sortie. La première couche cachée a des connexions récurrentes depuis le passé vers le futur, tandis que l’autre transmet les activations depuis le futur vers le passé (Fig. 35).
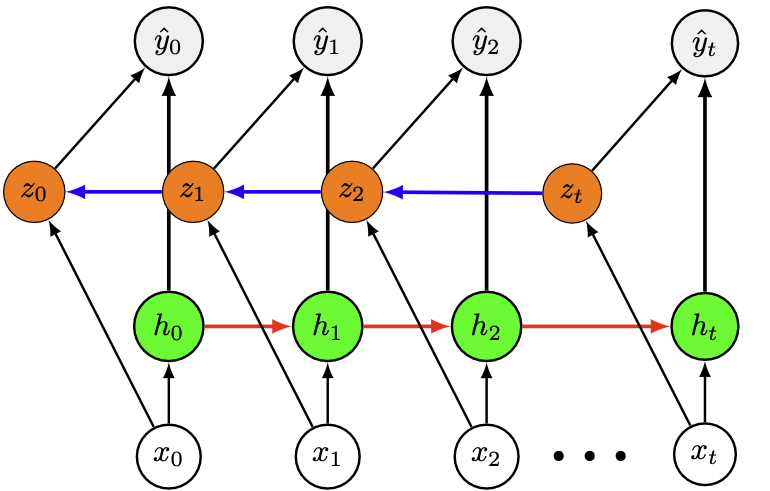
Fig. 35 Réseau bidirectionnel#
Étant données une entrée et une sortie du réseau (des séquences), le réseau peut être entraîné par rétropropagation après avoir été déplié :
où \(h_t\) (respectivement \(z_{t}\)) représente la valeur de la couche cachée dans le sens du temps (respectivement dans le sens inverse). Puisque le temps doit être fini dans les deux sens de parcours, les réseaux bidirectionnels ne peuvent traiter que des séquences finies.
Machines de Turing neuronales#
Les réseaux récurrents sont performants pour construire une représentation implicite de l’information, mais restent relativement peu adaptés à la conservation d’informations explicites (des dates précises par exemple). S’inspirant des mémoires de travail, théorisées par les neurosciences et qui sont responsables du raisonnement inductif et de la création de nouveaux concepts, l’idée est alors d’ajouter à ces modèles une mémoire de travail externe, ce qui permet de découpler la mémoire (assimilable à la RAM d’un ordinateur) des opérations liées à la tâche effectuée par le réseau (assimilable à la CPU). Puisque la mémoire des LSTM est distribuée dans chaque cellule, elle est donc liée au nombre de cellules et à la capacité de calcul et ce modèle ne répond pas directement au problème posé.
Graves et al. [4] proposent alors une architecture, appelée machine de Turing neuronale, constituée de deux éléments principaux : une mémoire et un contrôleur doté d’un mécanisme d’attention qui lit et écrit dans cette mémoire. Les accès mémoire sont ici des équivalents analogiques dérivables, pour permettre d’entraîner le contrôleur par descente de gradient. Typiquement, le contrôleur est un réseau de neurones ou un réseau récurrent type LSTM (Fig. 36).
Les têtes de lecture et d’écriture interagissent avec la mémoire. Chaque tête est contrôlée par un vecteur de poids, chaque composante définissant le degré d’interaction de la tête avec la zone mémoire correspondante. Un mécanisme de mise à jour de ces poids, composé de quatre opérations, est mis en place pour permettre l’apprentissage du réseau :
Le réseau s’intéresse tout d’abord aux zones mémoire proches d’une clé \(k_t\) donnée. Cela permet au modèle de retrouver une information spécifique, en recherchant si la zone mémoire \(M_t(i)\) est proche de la clé, au sens d’une similarité \(K\). Formellement, chaque poids correspondant à la zone mémoire \(i\) est calculé par \(w_t(i) = softmax(\beta_t K[k_t,M_t(i)])\).
Un mécanisme d’interpolation linéaire permet ensuite de mettre à jour les poids en fonction de leur valeur précédente (pour prendre plus ou moins en compte l’information issue de la clé, ou au contraire la valeur précédente du poids) : \(w_t(i)=g_t.w_t(i) + (1-g_t).w_{t-1}(i)\).
Un décalage par convolution translate ensuite les poids, à la manière du décalage de la tête dans une machine de Turing classique : \(w_t(i)=\displaystyle\sum_j w_t(j)\mathbf{s_t}(i-j)\) où \(\mathbf{s_t}\) est un vecteur qui définit un décalage des poids à l’instant \(t\).
Enfin, le vecteur de poids est focalisé : \(w_t(i) = w_t(i)^{\gamma_t}\), \(\gamma_t>1\).
Une fois que la tête a mis à jour les poids, elle interagit avec la mémoire :
Dans le cas de la tête de lecture, elle calcule une combinaison linéaire des zones mémoire, pondérées par les poids \(w_t(i)\) et produit le vecteur \(\mathbf{r_t}\), fourni au contrôleur de l’instant suivant.
Dans le cas de la tête d’écriture, le contenu de la mémoire est mis à jour selon la formule \(M_t(i) = M_{t-1}(i)(1-w_t(i)\mathbf{e_t})+w_t(i)\mathbf{a_t}\), où \(\mathbf{e_t}\) est un vecteur d’effacement, dont les composantes sont dans {0,1} et \(\mathbf{a_t}\) est un vecteur d’ajout.
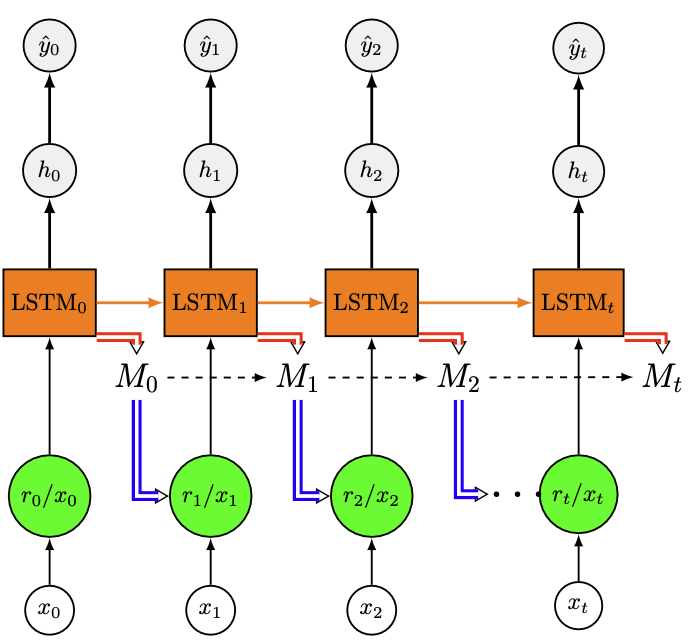
Fig. 36 Exemple de machine de Turing nuronale dépliée dans le temps, oà le contrôleur est un LSTM. Les accès en écriture du LSTM dans la mémoire sont représentés par des flèches rouges, les accès en lecture en bleu.#
Implémentation#
import pandas as pd
import numpy as np
import math
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from sklearn.preprocessing import MinMaxScaler
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
On s’intéresse aux données financières d’Apple (Fig. 37) et plus particulièrement
au prix d’une action à l’ouverture (open) et à la fermeture (close), par jour
au prix le plus bas (low) et haut (high), par jour
à l’ajustement de clôture (adj_close) et le volume de vente (volume), par jour.
df = pd.read_csv("./data/finance.csv",index_col=0)
column_names = list(df.columns.values)
df_plot = df.copy()
ncols = 2
nrows = int(round(df_plot.shape[1] / ncols, 0))
fig, ax = plt.subplots(nrows=nrows, ncols=ncols,sharex=True, figsize=(14, 7))
for i, ax in enumerate(fig.axes):
ax.plot(np.array(df_plot.iloc[:, i]))
ax.set_ylabel(column_names[i])
ax.tick_params(axis="x", rotation=30, labelsize=10, length=0)
ax.xaxis.set_major_locator(mdates.AutoDateLocator())
fig.tight_layout()
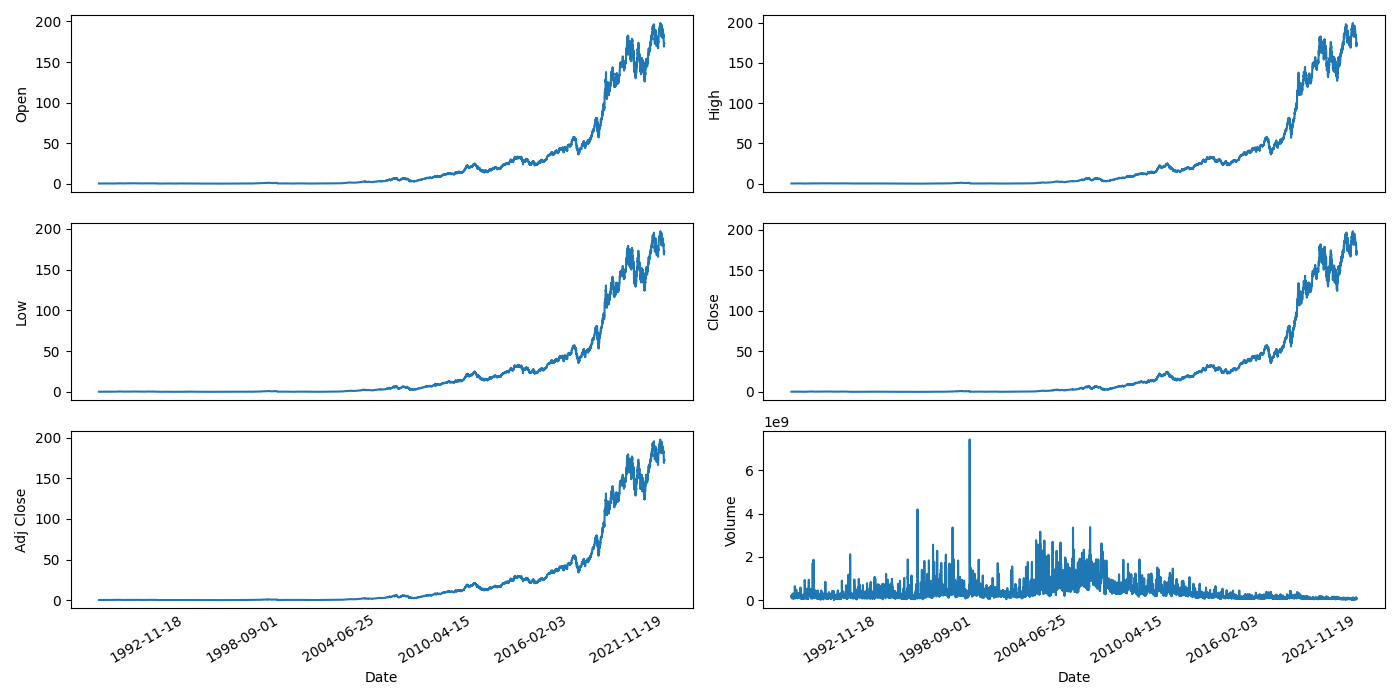
Fig. 37 Données financières d’Apple (source : Yahoo finance)#
On découpe les données en ensemble d’entraînement et de test, et on s’intéresse au prix à l’ouverture de l’action. On normalise ces données dans [0,1]
l = math.ceil(len(df) * .8)
train_data = df[:l].iloc[:,:1]
test_data = df[l:].iloc[:,:1]
dataset_test = test_data.Open.values
dataset_test = np.reshape(dataset_test, (-1,1))
scaler = MinMaxScaler(feature_range=(0,1))
x_train = scaler.fit_transform(dataset_train)
x_test = scaler.fit_transform(dataset_test)
On créé les séquences d’entraînement (de longueur 50 ici) et de test (de longueur 30)
l = 50
X_train, y_train = [], []
for i in range(len(x_train) - l):
X_train.append(x_train[i:i+l])
y_train.append(x_train[i+1:i+l+1])
X_train = torch.tensor(np.array(X_train) , dtype=torch.float32)
y_train = torch.tensor(np.array(y_train), dtype=torch.float32)
l = 30
X_test, y_test = [], []
for i in range(len(x_test) - l):
X_test.append(x_test[i:i+l])
y_test.append(x_test[i+1:i+l+1])
X_test = torch.tensor(np.array(X_test), dtype=torch.float32)
y_test = torch.tensor(np.array(y_test), dtype=torch.float32)
On créé ensuite le modèle. input_sizeest le nombre de caractéristiques de l’entrée à chaque pas de temps. hidden_sizeest le nombre d’unités du LSTM et num_layersle nombre de couches LSTM.
class LSTMModel(nn.Module):
def __init__(self, input_size, hidden_size, num_layers):
super(LSTMModel, self).__init__()
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)
self.linear = nn.Linear(hidden_size, 1)
def forward(self, x):
out, _ = self.lstm(x)
out = self.linear(out)
return out
On sélectionne le device d’entraînement, on instantie un modèle que l’on équipe d’une fonction de perte et d’un optimiseur.
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
input_size,num_layers,hidden_size,output_size = 1,2,64,1
model = LSTMModel(input_size, hidden_size, num_layers).to(device)
loss_fn = torch.nn.MSELoss(reduction='mean')
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
On définit les batchs, et on entraîne le réseau
batch_size = 16
train_dataset = torch.utils.data.TensorDataset(X_train, y_train)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_dataset = torch.utils.data.TensorDataset(X_test, y_test)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
num_epochs = 30
train_hist =[]
test_hist =[]
for epoch in range(num_epochs):
total_loss = 0.0
model.train()
for batch_X, batch_y in train_loader:
batch_X, batch_y = batch_X.to(device), batch_y.to(device)
predictions = model(batch_X)
loss = loss_fn(predictions, batch_y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
average_loss = total_loss / len(train_loader)
train_hist.append(average_loss)
# Validation sur l'ensemble de test
model.eval()
with torch.no_grad():
total_test_loss = 0.0
for batch_X_test, batch_y_test in test_loader:
batch_X_test, batch_y_test = batch_X_test.to(device), batch_y_test.to(device)
predictions_test = model(batch_X_test)
test_loss = loss_fn(predictions_test, batch_y_test)
total_test_loss += test_loss.item()
average_test_loss = total_test_loss / len(test_loader)
test_hist.append(average_test_loss)
x = np.linspace(1,num_epochs,num_epochs)
plt.plot(x,train_hist,scalex=True, label="Perte, entraînement")
plt.plot(x, test_hist, label="Perte, test")
plt.xlabel('epoch')
plt.ylabel('MSE')
plt.legend()
plt.tight_layout()
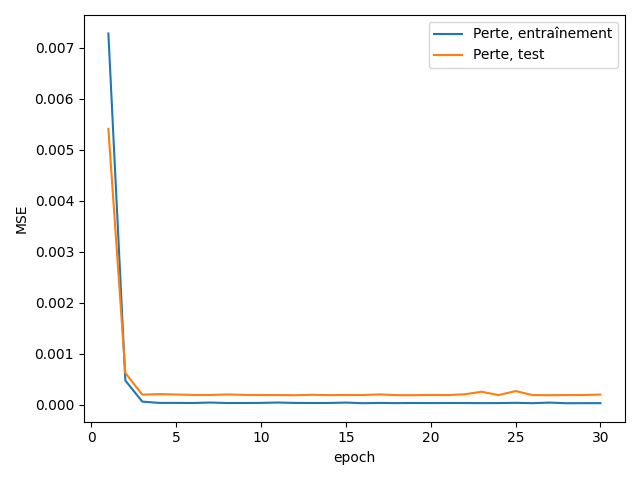
Fig. 38 Fonction de perte en entraînement et en test#
On utilise ensuite le modèle pour prédire les valeurs à l’ouverture de l’action sur les 30 jours suivants
nb_predire = 30
seq = X_test.squeeze().cpu().numpy()
# initialisation : 30 derniers pas de temps
historique = seq[-1]
val_predites = []
# Prédiction
with torch.no_grad():
for _ in range(nb_predire*2):
historique_tensor = torch.as_tensor(historique).view(1, -1, 1).float().to(device)
# Prédiction de la valeur suivante
val_predite = model(historique_tensor).cpu().numpy()[0, 0]
val_predites.append(val_predite[0])
# déplacement de l'historique
historique = np.roll(historique, shift=-1)
historique[-1] = val_predite
# dates futures
last_date = test_data.index[-1]
from pandas.tseries.offsets import DateOffset
future_dates = pd.date_range(start=pd.to_datetime(last_date) + pd.DateOffset(1), periods=nb_predire)
index_c = test_data.index.append(future_dates).map(str)
et on affiche le résultat (Fig. 39)
fig, ax = plt.subplots(1,1, figsize=(14, 5))
ax.tick_params(axis="x", rotation=30, labelsize=10, length=0)
ax.xaxis.set_major_locator(mdates.AutoDateLocator())
#Données test
plt.plot(test_data.index[-100:-nb_predire], test_data.Open[-100:-nb_predire], label = "Données test", color = "b")
val_reelles = scaler.inverse_transform(np.expand_dims(seq[-1], axis=0)).flatten()
# Données utilisées pour la prédiction
plt.plot(test_data.index[-nb_predire:], val_reelles, label='Valeurs réelles', color='green')
val_predites = scaler.inverse_transform(np.expand_dims(val_predites, axis=0)).flatten()
plt.plot(index_c[-2*nb_predire:], val_predites, label='Valeurs prédites', color='red')
plt.xlabel('Date')
plt.ylabel('Valeur')
plt.legend()
plt.title('Prévision')
plt.grid(True)
plt.tight_layout()
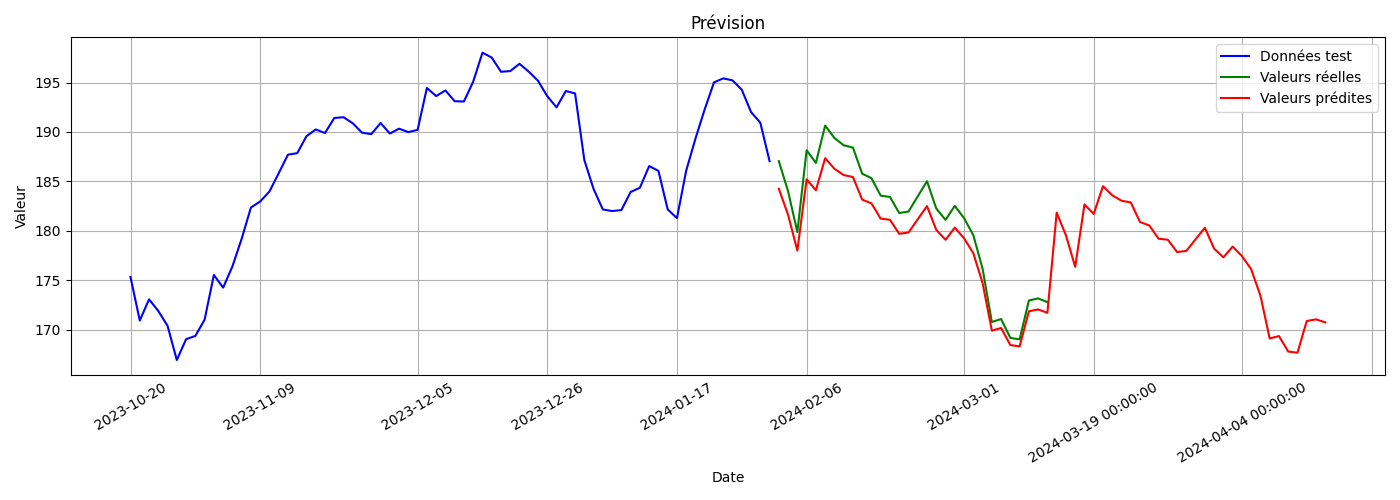
Fig. 39 Prédiction du modèle et valeurs réelles#
S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural Comput., 9(8):1735–1780, November 1997. URL: http://dx.doi.org/10.1162/neco.1997.9.8.1735, doi:10.1162/neco.1997.9.8.1735.
J Chung, Ç Gülçehre, K Cho, and Y Bengio. Empirical evaluation of gated recurrent neural networks on sequence modeling. CoRR, 2014. URL: http://arxiv.org/abs/1412.3555.
M. Schuster and K.K. Paliwal. Bidirectional recurrent neural networks. Trans. Sig. Proc., 45(11):2673–2681, November 1997. URL: http://dx.doi.org/10.1109/78.650093, doi:10.1109/78.650093.
A Graves, G Wayne, and I Danihelka. Neural turing machines. CoRR, 2014. URL: http://arxiv.org/abs/1410.5401.