Réseaux convolutifs#

Introduction#

Inspiration biologique#

Un réseau de neurones convolutif (CNN, Convolutional Neural Network) est un type de réseau de neurones artificiels acyclique à propagation avant, dans lequel le motif de connexion entre les neurones est inspiré par le cortex visuel des animaux. Les neurones de cette région du cerveau sont arrangés de sorte à ce qu’ils correspondent à des régions (appelés champs réceptifs) qui se chevauchent lors du pavage du champ visuel. Ils sont de plus organisés de manière hiérarchique, en couches (aire visuelle primaire V1, secondaire V2, puis aires V3, V4, V5 et V6, gyrus temporal inférieur), chacune des couches étant spécialisée dans une tâche, de plus en plus abstraite en allant de l’entrée vers la sortie. En simplifiant à l’extrême, une fois que les signaux lumineux sont reçus par la rétine et convertis en potentiels d’action :

  • L’aire primaire V1 s’intéresse principalement à la détection de contours, ces contours étant définis comme des zones de fort contraste de signaux visuels reçus.

  • L’aire V2 reçoit les informations de V1 et extrait des informations telles que la fréquence spatiale, l’orientation, ou encore la couleur.

  • L’aire V4, qui reçoit des informations de V2, mais aussi de V1 directement, détecte des caractéristiques plus complexes et abstraites liées par exemple à la forme.

  • Le gyrus temporal inférieur est chargé de la partie sémantique (reconnaissance des objets), à partir des informations reçues des aires précédentes et d’une mémoire des informations stockées sur des objets.

L’architecture et le fonctionnement des réseaux convolutifs sont inspirés par ces processus biologiques. Ces réseaux consistent en un empilage multicouche de perceptrons, dont le but est de prétraiter de petites quantités d’informations. Les réseaux convolutifs ont de larges applications dans la reconnaissance d’image et vidéo, les systèmes de recommandation et le traitement du langage naturel.

Un réseau convolutif se compose de deux types de neurones, agencés en couches traitant successivement l’information. Dans le cas du traitement de données de type images, on a ainsi :

  • des neurones de traitement, qui traitent une portion limitée de l’image (le champ réceptif) au travers d’une fonction de convolution;

  • des neurones de mise en commun des sorties dits d’agrégation totale ou partielle (pooling).

Un traitement correctif non linéaire est appliqué entre chaque couche pour améliorer la pertinence du résultat. L’ensemble des sorties d’une couche de traitement permet de reconstituer des images intermédiaires, dite cartes de caractéristiques (feature maps), qui servent de base à la couche suivante. Les couches et leurs connexions apprennent des niveaux d’abstraction croissants et extraient des caractéristiques de plus en plus haut niveau des données d’entrée.

Dans la suite, le propos sera illustré sur des images 2D en niveaux de gris, de taille \(n_1 \times n_2\) :

\[\begin{split}\begin{aligned} \mathbf{I} : [\![1,n_1]\!]\times [\![1, n_2]\!] &\rightarrow& \mathbb{R}\\ (i,j) &\mapsto& I_{i,j} \end{aligned}\end{split}\]

\(\mathbf{I}\) sera indifféremment vue comme une fonction ou une matrice.

Convolution discrète#

Pour reproduire la notion de champ réceptif, et ainsi permettre aux neurones de détecter des caractéristiques de petite taille mais porteurs d’information, l’idée est de laisser un neurone caché voir et traiter seulement une petite portion de l’image qu’il prend en entrée. L’outil retenu dans les réseaux convolutifs est la convolution discrète.

Definition 5 (Convolution discrète)

Soient \(h_1,h_2\in\mathbb{N}, \mathbf{K} \in \mathbb{R}^{(2h_1+1) \times (2h_2+1)}\). La convolution discrète de \(\mathbf{I}\) par le filtre \(\mathbf{K}\) est donnée par :

\[\begin{aligned} \label{eq:convolution} \left(\mathbf{K} \ast \mathbf{I}\right)_{r,s} = \displaystyle\sum _{u = -h_1} ^{h_1} \displaystyle\sum _{v = -h_2}^{h_2} K_{u,v} I_{r+u,s+v} \end{aligned}\]

où \(\mathbf{K}\) est donné par :

\[\begin{split}\begin{aligned} \mathbf{K} = \begin{pmatrix} K_{-h_1,-h_2} & \ldots & K_{-h_1,h_2}\\ \vdots & K_{0,0} & \vdots\\ K_{h_1,-h_2} & \ldots & K_{h_1,h_2}\\ \end{pmatrix}. \end{aligned}\end{split}\]

La taille du filtre \((2h_1+1) \times (2h_2+1)\) précise le champ visuel capturé et traité par \(\mathbf{K}\).
Lorsque \(\mathbf{K}\) parcourt \(\mathbf{I}\), le déplacement du filtre est réglé par deux paramètres de stride (horizontal et vertical). Un stride de 1 horizontal (respectivement vertical) signifie que \(\mathbf{K}\) se déplace d’une position horizontale (resp. verticale) à chaque application de l’équation précédente. Les valeurs de stride peuvent également être supérieures et ainsi sous-échantillonner \(\mathbf{I}\).

Le comportement du filtre sur les bords de \(\mathbf{I}\) doit également être précisé, par l’intermédiaire d’un paramètre de padding. Si l’image convoluée \(\left(\mathbf{K} \ast \mathbf{I}\right)\) doit posséder la même taille que \(\mathbf{I}\), alors \(2h_1\) lignes de 0 (\(h_1\) en haut et \(h_1\) en bas) et \(2h_2\) colonnes de 0 (\(h_2\) à gauche et \(h_2\) à droite) doivent être ajoutées. Dans le cas où la convolution est réalisée sans padding, l’image convoluée est de taille \((n_1-2h_1)\times (n_2-2h_2)\).

Définition des couches#

Nous introduisons ici les principaux types de couches utilisées dans les réseaux convolutifs. L’assemblage de ces couches permet de construire des architectures complexes pour la classification ou la régression.

Couche de convolution#

Soit \(l\in\mathbb{N}\) une couche de convolution. L’entrée de la couche \(l\) est composée de \(n^{(l-1)}\) cartes provenant de la couche précédente, de taille \(n_1^{(l-1)} \times n_2^{(l-1)}\). Dans le cas de la couche d’entrée du réseau (\(l = 1\)), l’entrée est l’image \(\mathbf{I}\). La sortie de la couche \(l\) est formée de \(n^{(l)}\) cartes de taille \(n_1^{(l)} \times n_2^{(l)}\). La \(i^{\text{e}}\) carte de la couche \(l\), notée \(\mathbf{Y_i^{(l)}}\), se calcule comme :

\[\begin{aligned} \mathbf{Y_i^{(l)}} = \mathbf{B^{(l)}_{i}} + \displaystyle\sum _{j = 1}^{n^{(l-1)}} \mathbf{K^{(l)}_{i,j}} \ast \mathbf{Y_j^{(l-1)}} \end{aligned}\]

où \(\mathbf{B_i^{(l)}}\) est une matrice de biais et \(\mathbf{K^{(l)}_{i,j}}\) est le filtre de taille \((2h_1^{(l)} + 1) \times (2h_2^{(l)} + 1)\) connectant la \(j^{\text{e}}\) carte de la couche \((l-1)\) à la \(i^{\text{e}}\) carte de la couche \(l\) (Fig. 10).

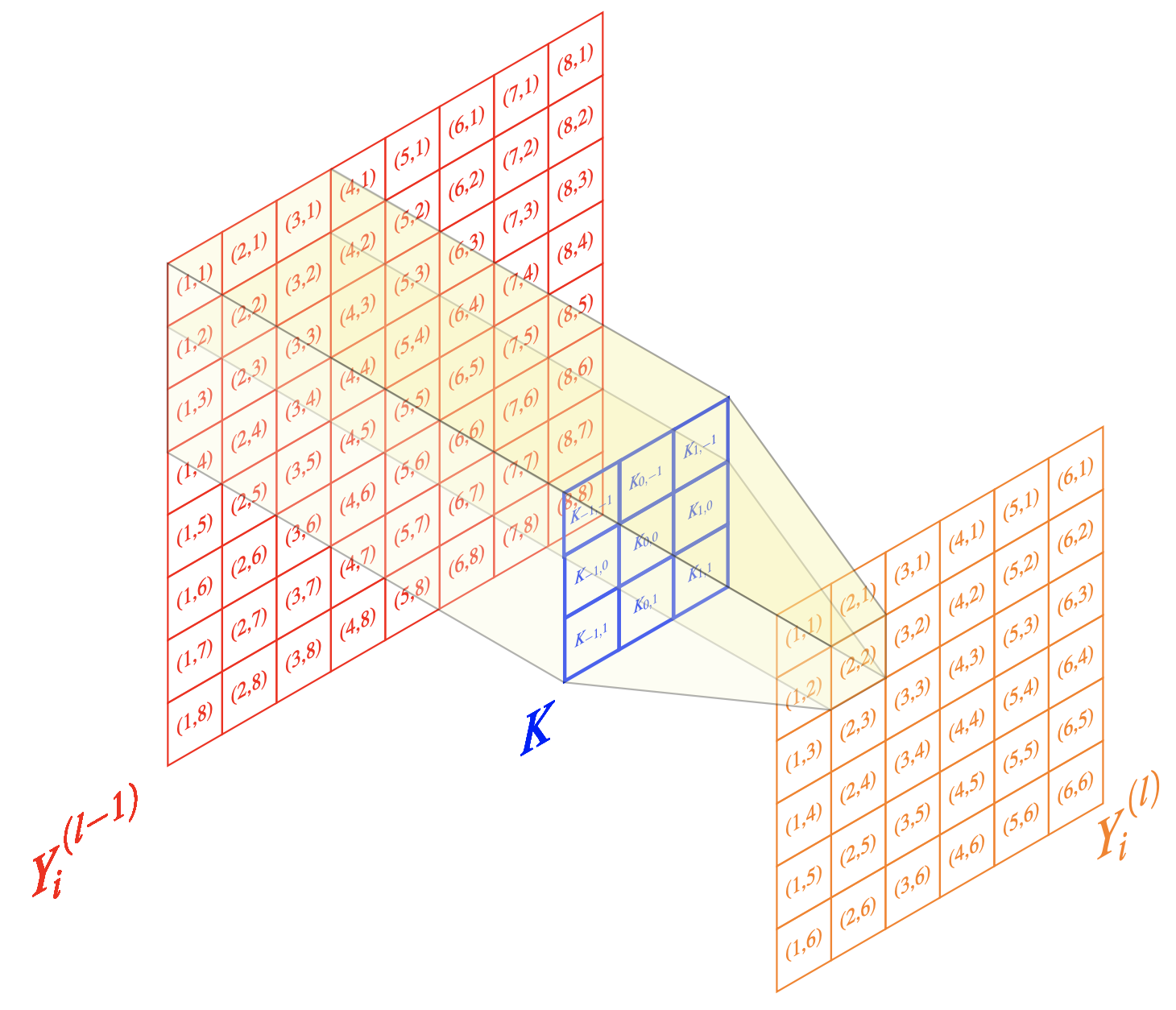
_images/cnn1.png

Fig. 10 Illustration des calculs effectués dans une opération de convolution discrète. Le pixel (2,2) de l’image \({\mathbf Y_i^{l}}\) est une combinaison linéaire des pixels \((i,j)\in[\![1,3]\!]^2\) de \({\mathbf Y_i^{l-1}}\) les coefficients de la combinaison étant portés par le filtre \(\mathbf K\).#

\(n_1^{(l)}\) et \(n_2^{(l)}\) doivent prendre en compte les effets de bords : lors du calcul de la convolution, seuls les pixels dont la somme est définie avec des indices positifs doivent être traités. Dans le cas où le padding n’est pas utilisé, les cartes de sortie ont donc une taille de \(n_1^{(l)} = n_1^{(l-1)} - 2h_1^{(l)}\) et \(n_2^{(l)} = n_2^{(l-1)} - 2h_2^{(l)}\).

Souvent, les filtres utilisés pour calculer \(\mathbf{Y_i^{(l)}}\) sont les mêmes, i.e. \(\mathbf{K_{i,j}^{(l)}} = \mathbf{K _{i,k}^{(l)}}\) pour \(j \neq k\). De plus, la somme dans l’équation de la convolution peut être conduite sur un sous-ensemble des cartes d’entrée.

Il est possible de mettre en correspondance la couche de convolution, et l’opération qu’elle effectue, avec un perceptron multicouche. Pour cela, il suffit de réécrire l’équation : chaque carte \(\mathbf{Y_i^{(l)}}\) de la couche \(l\) est formée de \(n_1^{(l)} \cdot n_2^{(l)}\) neurones organisés dans un tableau à deux dimensions. Le neurone en position \((r,s)\) calcule :

\[\begin{split}\begin{aligned} \left(\mathbf{Y_i^{(l)}}\right)_{r,s} &= \left(\mathbf{B_i^{(l)}}\right)_{r,s} + \displaystyle\sum _{j = 1}^{n^{(l-1)}} \left(\mathbf{K^{(l)}_{i,j} }\ast \mathbf{Y_j^{(l-1)}}\right)_{r,s}\\ &= \left(\mathbf{B_i^{(l)}}\right)_{r,s} + \displaystyle\sum _{j = 1}^{n^{(l-1)}} \displaystyle\sum _{u = - h_1^{(l)}} ^{h_1^{(l)}} \displaystyle\sum _{v = - h_2^{(l)}} ^{h_2^{(l)}} \left(\mathbf{K^{(l)}_{i,j}}\right)_{u,v} \left(\mathbf{Y_j^{(l-1)}}\right)_{r+u,s+v} \end{aligned}\end{split}\]

Les paramètres du réseau à entraîner (poids) peuvent alors être trouvés dans les filtres \(\mathbf{K^{(l)}_{i,j}}\) et les matrices de biais \(\mathbf{B_i^{(l)}}\).

Comme nous le verrons plus loin, un sous-échantillonnage est utilisé pour diminuer l’influence du bruit et des distorsions dans les images. Le sous-échantillonnage peut être également réalisé simplement avec des paramètres de stride, en sautant un nombre fixe de pixels dans les dimensions horizontale (saut \(s_1^{(l)}\)) et verticale (saut \(s_2^{(l)}\)) avant d’appliquer de nouveau le filtre. La taille des images de sortie est alors :

\[\begin{aligned} n_1^{(l)} = \frac{n_1^{(l-1)} - 2h_1^{(l)}}{s_1^{(l)} + 1}\quad \text{ et }\quad n_2^{(l)} = \frac{n_2^{(l-1)} - 2h_2^{(l)}}{s_2^{(l)} + 1}. \end{aligned}\]

Un point clé des réseaux convolutifs est d’exploiter la corrélation spatiale des données. L’utilisation des noyaux permet d’alléger le modèle, plutôt que d’utiliser des couches complètement connectées.

Couche non linéaire#

Pour augmenter le pouvoir d’expression des réseaux profonds, on utilise des couches non linéaires. Les entrées d’une couche non linéaire sont \(n^{(l-1)}\) cartes et ses sorties \(n^{(l)} = n^{(l-1)}\) cartes \(\mathbf{Y_i^{(l)}}\), de taille \(n_1^{(l-1)} \times n_2^{(l-1)}\) telles que \(n_1^{(l)} = n_1^{(l-1)}\) et \(n_2^{(l)} = n_2^{(l-1)}\), données par \(\mathbf{Y_i^{(l)}}\) = \(f \left(\mathbf{Y_i^{(l-1)}}\right)\), où \(f\) est la fonction d’activation utilisée dans la couche \(l\).

La Fig. 3 du cours sur les perceptrons multicouches présente quelques fonctions d’activation classiques.

En apprentissage profond, il a été reporté que la sigmoïde et la tangente hyperbolique avaient des performances moindres que la fonction d’activation softsign :

\[\begin{aligned} \mathbf{Y_i^{(l)}} = \frac{1}{1+ \left|\mathbf{Y_i^{(l-1)}} \right |}. \end{aligned}\]

En effet, les valeurs des pixels des cartes \(\mathbf{Y_i^{(l-1)}}\) arrivant près des paliers de saturation de ces fonctions donnent des gradients faibles, qui ont tendance à s’annuler (problème du gradient évanescent ou vanishing gradient) lors de la phase d’apprentissage par rétropropagation du gradient. Une autre fonction, non saturante elle, est très largement utilisée. Il s’agit de la fonction ReLU (Rectified Linear Unit) [1] :

\[\begin{aligned} \mathbf{Y_i^{(l)}} = max\left (0,\mathbf{Y_i^{(l-1)}}\right ) \end{aligned}\]

Les neurones utilisant la fonction ReLU sont appelés neurones linéaires rectifiés. Glorot et Bengio [2] ont montré que l’utilisation d’une couche ReLU en tant que couche non linéaire permettait un entraînement efficace de réseaux profonds sans pré-entraînement non supervisé. Plusieurs variantes de cette fonction existent, par exemple pour assurer une différentiabilité en 0 ou pour proposer des valeurs non nulles pour des valeurs négatives de l’argument.

Couches de normalisation#

La normalisation prend aujourd’hui une place de plus en plus importante, notamment depuis les travaux de Ioffe et Szegedy [3]. Les auteurs suggèrent qu’un changement dans la distribution des activations d’un réseau profond, résultant de la présentation d’un nouveau mini batch d’exemples, ralentit le processus d’apprentissage. Pour pallier ce problème, chaque activation du mini batch est centrée et normée (variance unité), la moyenne et la variance étant calculées sur le mini batch entier, indépendamment pour chaque activation. Des paramètres d’offset \(\beta\) et multiplicatif \(\gamma\) sont alors appliqués pour normaliser les données d’entrée (Algorithm 5).

Algorithm 5 (Normalisation par batch sur la présentation d’un mini batch \(\mathcal{B}\))

Entrées : valeurs de l’activation \(x\) sur un mini batch \(\mathcal{B} = \{x_1\cdots x_m\}\), Paramètres \(\beta,\gamma\) à apprendre

Sortie : Données normalisées \(\{y_1\cdots y_m\}=BatchNorm_{\gamma,\beta}(x_1\cdots x_m)\)

  1. \(\mu_\mathcal{B} = \frac{1}{m}\displaystyle\sum_{i=1}^m x_i\)

  2. \(\sigma^2_\mathcal{B} = \frac{1}{m}\displaystyle\sum_{i=1}^m \left (x_i-\mu_\mathcal{B}\right )^2\)

  3. Pour \(i=1\) à \(m\)

    1. \(y_i = \gamma \frac{x_i-\mu_\mathcal{B}}{\sqrt{\sigma^2_\mathcal{B}+\epsilon}}+\beta\)

Lorsque la descente de gradient est achevée, un post apprentissage est appliqué dans lequel la moyenne et la variance sont calculées sur l’ensemble d’entraînement et remplacent \(\mu_\mathcal{B}\) et \(\sigma^2_\mathcal{B}\) (Algorithm 6).

Algorithm 6 (Normalisation par batch d’un réseau)

{ Entrées : {un réseau \(N\), un ensemble d’activations \(\{x^1\cdots x^K\}\)

  1. \(N_n=N\)

  2. Pour \(i=1\) à \(K\)

    1. Calculer \(y^i=BN_{\gamma,\beta}(x^i)\) à l’aide de l”Algorithm 5

    2. Modifier chaque couche de \(N_n\) : l’entrée \(y^i\) remplace l’entrée \(x^i\)

  3. Entraîner \(N_n\) pour optimiser les paramètres de \(N\) et \((\gamma^i,\beta^i)_{i\in[\![1,K]\!]}\)

  4. \(N^f = N_n\)

  5. Pour \(i=1\) à \(K\)

    1. Utiliser \(N^f\) sur des batchs \(\mathcal{B}\) de taille \(m\)

    2. Calculer la moyenne des moyennes \(\bar{x^i}\) et des variances \(Var(x^i)\)

    3. Remplacer dans \(N^f\) la transformation \(y^i=BN_{\gamma,\beta}(x^i)\) par

\[y^i=\frac{\gamma^i}{\sqrt{Var(x^i)+\epsilon}}x^i+\left(\beta^i -\frac{\gamma^i \bar{x^i}}{\sqrt{Var(x^i)+\epsilon}}\right)\]

Couche d’agrégation et de sous-échantillonnage#

Le sous-échantillonnage (pooling) des cartes obtenues par les couches précédentes a pour objectif d’assurer une robustesse au bruit et aux distorsions.

La sortie d’une couche d’agrégation \(l\) (Fig. 11) est composée de \(n^{(l)} = n^{(l-1)}\) cartes de taille réduite. En général, l’agrégation est effectuée en déplaçant dans les cartes d’entrée une fenêtre de taille \(2p \times 2p\) toutes les \(q\) positions (il y a recouvrement si \(q < p\) et non recouvrement sinon), et en calculant, pour chaque position de la fenêtre, une seule valeur, affectée à la position centrale dans la carte de sortie.

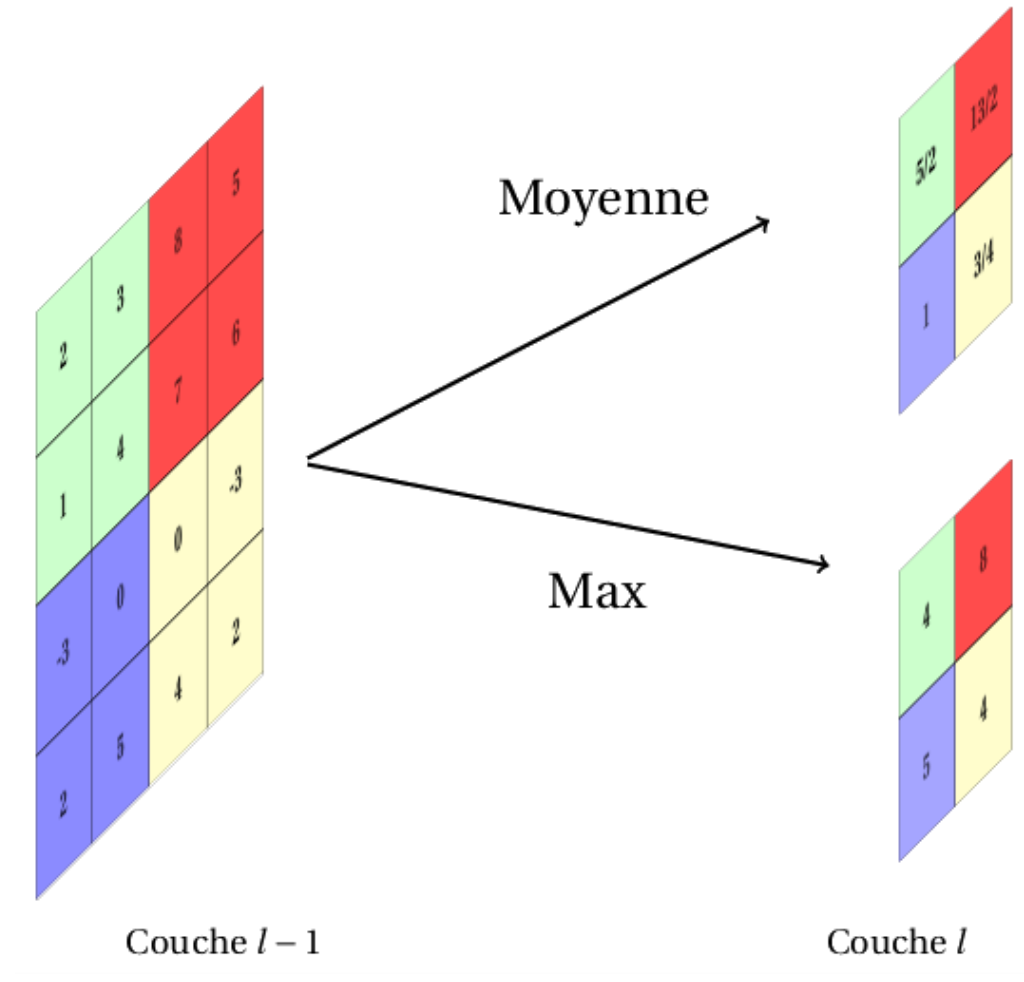
_images/pooling.png

Fig. 11 Couche d’agrégation et de sous-échantillonnage \(l\). Chacune des \(n^{(l−1)}\) cartes de la couche \(l-1\) est traitée individuellement. Chaque neurone des \(n^(l) = n^{(l−1)}\) cartes de sortie est la moyenne (ou le maximum) des valeurs contenues dans une fenêtre de taille donnée dans la carte correspondante de la couche \(l-1\).#

On distingue généralement deux types d’agrégation :

  • La moyenne : on utilise un filtre \(\mathbf{K_B}\) de taille \((2h_1 + 1)\times (2h_2 + 1)\) défini par

    \[\left(\mathbf{K_B}\right)_{r,s} = \frac{1}{(2h_1 + 1)(2h_2 + 1)}\]

  • Le maximum : la valeur maximum dans la fenêtre est retenue.

Le maximum est souvent utilisé pour assurer une convergence rapide durant la phase d’entraînement. L’agrégation avec recouvrement, elle, semble assurer une réduction du phénomène de surapprentissage

Couche complètement connectée#

Si \(l\) et \((l-1)\) sont des couches complètement connectées, l’équation :

\[\begin{aligned} z_i^{(l)} = \sum _{k = 0} ^{m^{(l-1)}} w_{i,k}^{(l)} y_k^{(l-1)}\quad \text{ où }\quad \mathbf{Z^{(l)}} = \mathbf{W^{(l)}} \mathbf{Y^{(l-1)}} \end{aligned}\]

avec \(\mathbf{Z^{(l)}}\), \(\mathbf{W^{(l)}}\) et \(\mathbf{Y^{(l-1)}}\) les représentations vectorielle et matricielle des entrées \(z_i^{(l)}\), des poids \(w_{i,k}^{(l)}\) et des sorties \(y_k^{(l-1)}\), permet de relier ces deux couches.

Dans le cas contraire, la couche \(l\) attend \(n^{(l-1)}\) entrées de taille \(n_1^{(l-1)} \times n_2^{(l-1)}\) et le \(i^{\text{e}}\) neurone de la couche \(l\) calcule :

\[\begin{aligned} y_i^{(l)} = f\left(z_i^{(l)}\right)\quad\text{ avec }\quad z_i^{(l)} = \displaystyle\sum _{j = 1}^{n^{(l-1)}} \displaystyle\sum _{r = 1} ^{n_1^{(l-1)}} \displaystyle\sum _{s = 1}^{n_2^{(l-1)}} w_{i,j,r,s}^{(l)} \left(\mathbf{ Y_j^{(l-1)}} \right)_{r,s} \end{aligned}\]

où \(w_{i,j,r,s}^{(l)}\) est le poids connectant le neurone en position \((r,s)\) de la \(j^{\text{e}}\) carte de la couche \((l - 1)\) au \(i^{\text{e}}\) neurone de la couche \(l\).

En pratique, les réseaux convolutifs sont utilisés pour apprendre une hiérarchie dans les données et la (ou les) couche(s) complètement connectée(s) est(sont) utilisée(s) en bout de réseau pour des tâches de classification ou de régression.

Une couche de classification classiquement mise en œuvre utilise le classifieur softmax, qui généralise la régression logistique au cas multiclasse (\(k\) classes). L’ensemble d’apprentissage \({\mathcal E}_a = \left \{(\mathbf{x^{(i)}}, y^{(i)}),i \in[\![1,m]\!]\right \}\) est donc tel que \(y^{(i)}\in[\![1,k]\!]\) et le classifieur estime la probabilité \(P(y^{(i)}=j |\mathbf{x^{(i)}})\) pour chaque classe \(j\in [\![1,k]\!]\). Le classifieur softmax calcule cette probabilité selon :

\[\forall j\in[\![1,k]\!]\quad P(y^{(i)}=j | \mathbf{x^{(i)}},\mathbf{W}) = \frac{e^{\mathbf{W_j^\top x^{(i)}}}}{\displaystyle\sum_{l=1}^k e^{\mathbf{W_l^\top}\mathbf{x^{(i)}}}}\]

où \(\mathbf{W}\) est la matrice des paramètres du modèle (les poids). Ces paramètres sont obtenus en minimisant une fonction de coût, qui peut par exemple s’écrire :

\[J(\mathbf{W}) =- \frac{1}{m}\displaystyle\sum_{i=1}^m \displaystyle\sum_{j=1}^k \mathbb{I}_{y^{(i)}=j}log\left ( \frac{e^{\mathbf{W_j^\top x^{(i)}}}}{\displaystyle\sum_{l=1}^k e^{\mathbf{W_l^\top x^{(i)}}}}\right ) + \frac{\lambda}{2}\displaystyle\sum_{i=1}^n \displaystyle\sum_{j=1}^k W_{ji}^2 \]

où \(\lambda\) est un paramètre de régularisation contrôlant le second terme du coût qui pénalise les grandes valeurs des poids (régularisation \(\ell_2\)).

Régularisation#

Un des enjeux principaux en apprentissage automatique est de construire des algorithmes ayant une bonne capacité de généralisation. Les stratégies mises en œuvre pour arriver à cette fin rentrent dans la catégorie générale de la régularisation et de nombreuses méthodes sont aujourd’hui proposées en ce sens. La régularisation a déjà été abordée dans le chapitre consacré aux perceptrons multicouches (voir section Régularisation). Nous faisons ici un focus sur trois stratégies largement utilisées en apprentissage profond.

Régularisation de la fonction de coût#

L’équation précédente est un exemple de régularisation de la fonction de coût, utilisée lors de la phase d’entraînement. À la fonction d’erreur est ajoutée une fonction des poids du réseau, qui peut prendre de multiples formes. Les deux principales stratégies sont :

  • La régularisation \(\ell_2\) (ou ridge regression), qui force les poids à avoir une faible valeur absolue : un terme de régularisation fonction de la norme \(\ell_2\) de la matrice des poids est ajouté. On parle souvent de weight decay.

  • La régularisation \(\ell_1\), qui tend à rendre épars le réseau profond, i.e. à imposer à un maximum de poids de s’annuler. Un terme de régularisation, somme pondérée des valeurs absolues des poids, est ajouté à la fonction objectif.

Dropout#

Les techniques de dropout se rapprochent des stratégies classiques de bagging en apprentissage automatique. L’objectif est d’entraîner un ensemble constitué de tous les sous-réseaux qui peuvent être construits en supprimant des neurones (hors neurones d’entrée et de sortie) du réseau initial. Si le réseau comporte \(|\mathbf{W}|\) neurones cachés, il existe ainsi \(2^{|\mathbf{W}|}\) modèles possibles. En pratique, les neurones cachés se voient perturbés par un bruit binomial, qui a pour effet de les empêcher de fonctionner en groupe et de les rendre, au contraire, plus indépendants. Le phénomène de surapprentissage est ainsi fortement réduit sur le réseau, qui doit décomposer les entrées en caractéristiques pertinentes, indépendamment les unes des autres. Les réseaux construits par dropout partagent partiellement leurs paramètres, ce qui diminue l’empreinte mémoire de la méthode.

Lors de la phase de prédiction, le réseau complet est utilisé, mais les neurones cachés sont pondérés par la fraction de bruit utilisé pendant l’apprentissage (i.e. pour chaque neurone le nombre de fois où il a été supprimé d’un sous-réseau, rapporté au nombre total de réseaux), afin de conserver la valeur moyenne des activations des neurones identiques à celles durant l’apprentissage.

Notons qu’il est également possible d’éteindre non pas un neurone, mais un poids. La stratégie correspondante est appelée DropConnect.

Partage de paramètres#

La régularisation de la fonction de coût permet d’imposer aux poids certaines contraintes (par exemple de rester faibles en amplitude pour la régularisation \(\ell_2\), ou de s’annuler pour la régularisation \(\ell_1\)). Il peut également être intéressant d’imposer certains a priori sur les poids, par exemple une dépendance entre les valeurs des paramètres.

Une dépendance classique consiste à imposer que les valeurs de certains poids soient proches les unes des autres (dans le cas par exemple où deux modèles de classification \(M_1\) et \(M_2\), de paramètres \(\mathbf{W_1}\) et \(\mathbf{W_2}\), opèrent sur des données similaires et sur des classes identiques) et, là encore, une stratégie de pénalisation de la fonction objectif peut être utilisée. Cependant, il est plus courant dans ce cas d’imposer que les paramètres soient égaux (dans l’exemple précédent imposer \(\mathbf{W_1}=\mathbf{W_2}\)) et d’arriver à une stratégie dite de partage des paramètres. Dans le cas des réseaux convolutifs utilisés en vision, cette régularisation est assez intuitive puisque les entrées (images) possèdent de nombreuses propriétés invariantes par transformations affines (une image de voiture reste une image de voiture, même si l’image est translatée ou mise à l’échelle (Fig. 12)). Le réseau exploite alors ce partage de paramètres, en calculant une même caractéristique (un neurone et son poids) à différentes positions dans l’image. De ce fait, le nombre de paramètres est drastiquement réduit, ainsi que l’empreinte mémoire du réseau appris.

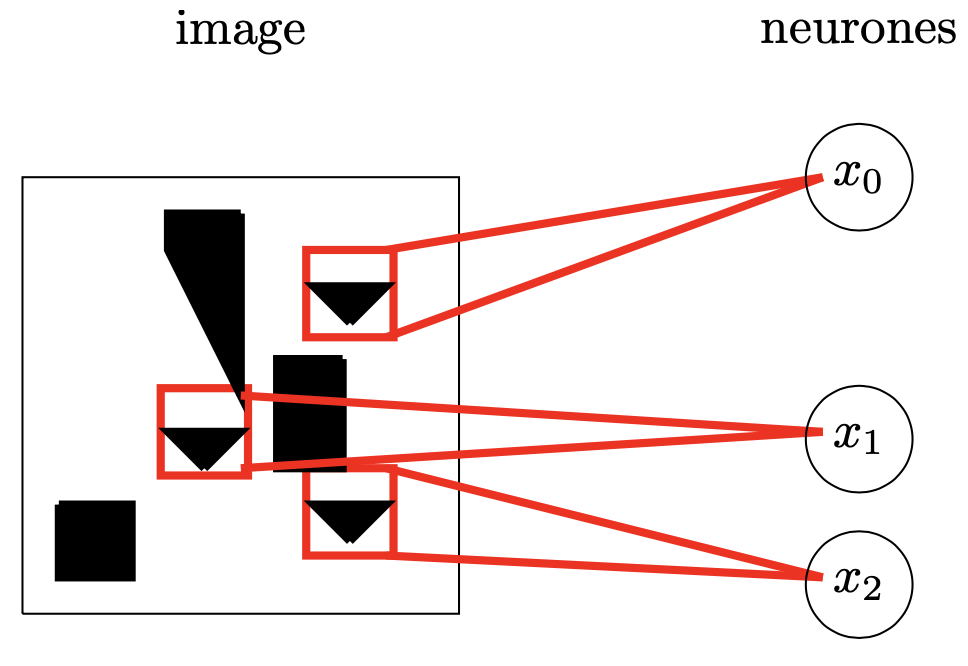
_images/partage.png

Fig. 12 Partage de paramètres : les neurones voient des champs réceptifs distincts, mais partagent les mêmes paramètres (poids). Leur capacité de détection d’un triangle restera la même, quelle que soit la position de l’objet dans l’image.#

Initialisation#

Une initialisation convenable des poids est essentielle pour assurer une convergence de la phase d’entraînement. Un choix arbitraire des poids (à zéro, à de petites ou grandes valeurs aléatoires) peut ralentir, voire causer de la redondance dans le réseau (problème de la symétrie). Ces aspects ont déjà été abordés dans la section Initialisation des poids), où l’initialisation de Xavier

\[\begin{aligned} - \frac{\sqrt{6}}{\sqrt{m^{(l-1)} + m^{(l)}}} < w_{i,j}^{(l)} < \frac{\sqrt{6}}{\sqrt{m^{(l-1)} + m^{(l)}}}. \end{aligned}\]

a été notamment détaillée.

Apprentissage#

La présence de nombreuses couches cachées va permettre de calculer des caractéristiques beaucoup plus complexes et informatives des entrées. Chaque couche calculant une transformation non linéaire de la couche précédente, le pouvoir de représentation de ces réseaux s’en trouve amélioré. On peut par exemple montrer qu’il existe des fonctions qu’un réseau à \(k\) couches peut représenter de manière compacte (avec un nombre de neurones cachés qui est polynomial en le nombre des entrées), alors qu’un réseau à \(k-1\) couches ne peut pas le faire, à moins d’avoir une combinatoire exponentielle sur le nombre de neurones cachés.

Le problème de l’entraînement#

Si l’intérêt de ces réseaux est manifeste, la complexité de leur utilisation vient de l’étape d’apprentissage. Jusqu’à récemment, l’algorithme utilisé était classique et consistait en une initialisation aléatoire des poids du réseau, suivie d’un entraînement sur un ensemble d’apprentissage, en minimisant une fonction objectif. Cependant, dans le cas des réseaux profonds, cette approche peut ne pas être adaptée :

  • Les données étiquetées doivent être en nombre suffisant pour permettre un entraînement efficace, d’autant plus que le réseau est complexe. Dans le cas contraire, un surapprentissage peut notamment être induit.

  • Sur un tel réseau, l’apprentissage se résume à l’optimisation d’une fonction fortement non convexe, qui amène presque sûrement à des minima locaux lorsque des algorithmes classiques sont utilisés.

  • Dans l’étape de rétropropagation, les gradients diminuent rapidement à mesure que le nombre de couches cachées augmente. La dérivée de la fonction objectif par rapport à \(\mathbf{W}\) devient alors très faible à mesure que le calcul se rétropropage vers la couche d’entrée. Les poids des premières couches changent donc très lentement et le réseau n’est plus en capacité d’apprendre. Ce problème est connu sous le nom de problème de gradient évanescent (vanishing gradient).

L’algorithme principalement utilisé pour l’apprentissage des réseaux convolutifs reste la rétropropagation du gradient. Le choix de la fonction objectif, de sa régularisation, de la méthode d’optimisation (descente de gradient, méthodes à taux d’apprentissage adaptatifs telles qu’AdaGrad, RMSProp ou Adam) et des paramètres associés, ou des techniques de présentation des exemples (batchs, minibatchs) sont autant de facteurs importants permettant aux modèles non seulement de converger vers un optimum local satisfaisant, mais également de proposer un modèle final ayant une bonne capacité de généralisation.

Aujourd’hui, de nombreux réseaux, déjà entraînés, sont mis à disposition (voir section Utilisation de réseaux existants). En effet, ces entraînements nécessitent de grandes bases d’apprentissage (type ImageNet) et une puissance de calcul assez élevée (GPUs obligatoires). Pour le traitement de problèmes précis, des méthodes existent, qui partent de ces réseaux préentraînés et les modifient localement pour, par exemple, apprendre de nouvelles classes d’images non encore vues par le réseau. L’idée sous-jacente est que les premières couches capturent des caractéristiques bas niveau et que la sémantique vient avec les couches profondes. Ainsi, dans un problème de classification, où les classes n’ont pas été apprises, on peut supposer qu’en conservant les premières couches on extraira des caractéristiques communes des images (bords, colorimétrie,…) et qu’en changeant les dernières couches (information sémantique et haut niveau et étage de classification), c’est-à-dire en réapprenant les connexions, on spécifiera le nouveau réseau pour la nouvelle tâche de classification. Cette approche rentre dans le cadre des méthodes de transfer learning et de fine tuning, cas particulier d’adaptation de domaine :

  • Les méthodes de transfert prennent un réseau déjà entraîné, enlèvent la dernière couche complètement connectée et traitent le réseau restant comme un extracteur de caractéristiques. Un nouveau classifieur, la dernière couche, est alors entraîné sur le nouveau problème (Fig. 13).

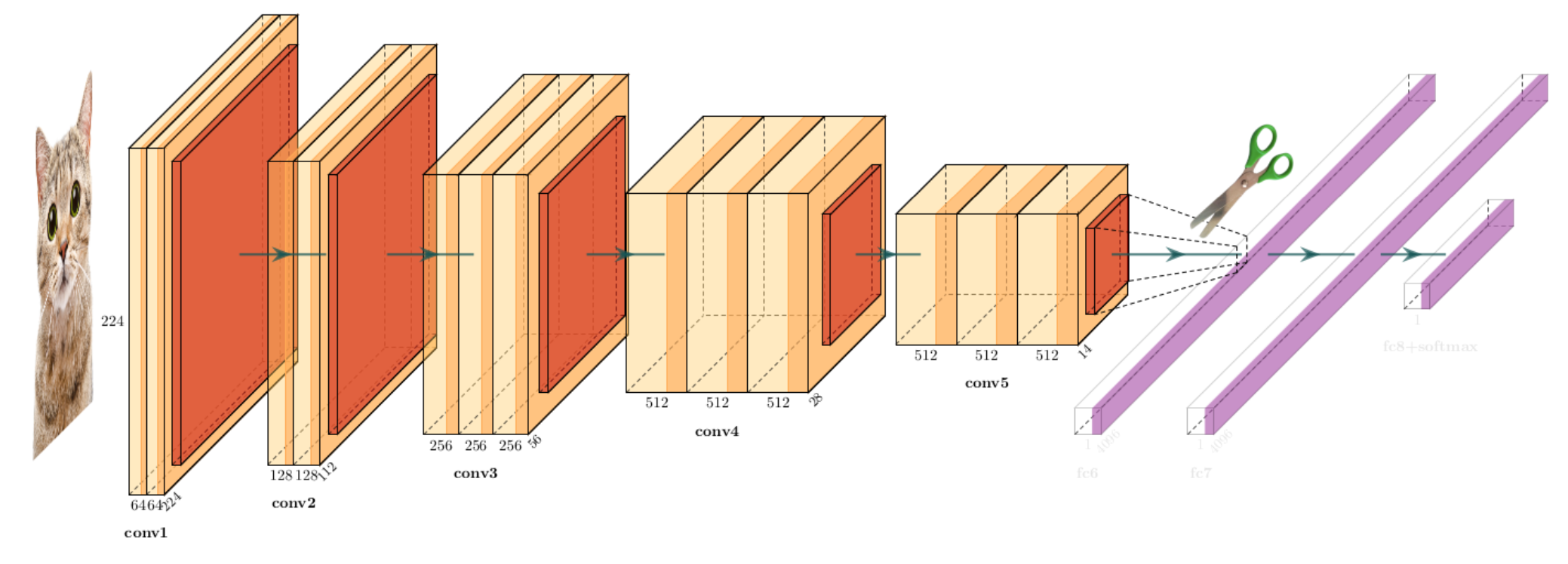
_images/transferLearning.png

Fig. 13 Illustration de la technique de transfer Learning. Le réseau appris à classer des images de chat est amputé de sa partie classification. Un nouveau classifieur est mis au bout du réseau, dont les poids sont entraînés sur la nouvelle tâche de classification.#

  • Les méthodes de fine tuning ré-entraînent tout ou partie d’un réseau (suivant les données disponibles) et conservent les poids non ré-entrainés.

Plusieurs facteurs influent sur le choix de la méthode à utiliser : la taille des données d’apprentissage du nouveau problème et la ressemblance du nouveau jeu de données avec celui qui a servi à entraîner le réseau initial :

  • Pour un jeu de données similaire de petite taille, on utilise du transfer learning, avec un classifieur utilisé sur les caractéristiques calculées sur les dernières couches du réseau initial.

  • Pour un jeu de données de petite taille et un problème différent, on utilise du transfer learning, avec un classifieur utilisé sur les caractéristiques calculées sur les premières couches du réseau initial.

  • Pour un jeu de données, similaire ou non, de grande taille, on utilise le fine tuning.

Notons qu’il est toujours possible d’augmenter la taille du jeu de données par des technique d’augmentation de données.

Dans le cas où un réseau ad hoc doit être construit et où une base d’apprentissage suffisante est disponible, l’entraînement par optimisation reste possible mais peut nécessiter des ressources de calcul importantes. De plus, il a été montré que :

  • le transfer Learning ou le fine tuning permettaient souvent d’aboutir à de meilleures performances que l’entraînement depuis un réseau initial aléatoire (on se sert des poids du réseau pré entraîné comme initialisation, plutôt qu’une initialisation type Xavier).

  • le fine tuning améliorait la capacité de généralisation du réseau.

Visualisation du mécanisme des réseaux convolutifs#

Le mécanisme interne des réseaux convolutifs est mal compris et l’analyse des raisons qui font que leur puissance de prédiction est importante n’est pas aisée. S’il est toujours possible de rétroprojeter les activations depuis la première couche de convolution, les couches d’agrégation et de rectification empêchent de comprendre le fonctionnement des couches suivantes, ce qui peut être gênant dans la construction et l’amélioration de ces réseaux.

Les méthodes de visualisation du fonctionnement des réseaux convolutifs peuvent être rangées en trois catégories, décrites brièvement dans les paragraphes suivants.

Méthodes de visualisation de base#

Les méthodes les plus simples consistent à visualiser les activations lors du passage d’une image dans le réseau. Pour des activations type ReLU, ces activations sont ininterprétables au début de l’entraînement, mais à mesure que ce dernier progresse, les cartes d’activation \(\mathbf{Y_i^{(l)}}\) deviennent localisées et éparses.

Il est également possible de visualiser les filtres des différentes couches de convolution (Fig. 14). Les filtres des premières couches agissent comme des détecteurs de bords et coins et, à mesure que l’on s’enfonce dans le réseau, les filtres capturent des concepts haut niveau comme des objets ou encore des visages.

Citons encore d’autres méthodes qui proposent de visualiser les dernières couches (les couches complètement connectées) de grande dimension (par exemple 4096 pour AlexNet) via une méthode de réduction de dimension.

_images/visufiltres.png

Fig. 14 Visualisation des filtres de la première couche d’AlexNet (à gauche, 64 filtres 11\(\times\)11) et de ResNet-18 (à droite, 64 filtres 7\(\times 7\)).#

Méthodes fondées sur les activations#

Plusieurs stratégies peuvent être adoptées pour sonder le fonctionnement d’un réseau convolutif, en utilisant les informations portées par les cartes \(\mathbf{Y_i^{(l)}}\), parmi lesquelles :

  • Utiliser des couches de convolution transposée (improprement appelées parfois couches de déconvolution), ajoutées à chaque couche de convolution du réseau. Étant données les cartes d’entrée de la couche \(l\), les cartes de sortie \(\mathbf{Y_i^{(l)}}\) sont envoyées dans la couche de convolution transposée correspondante au niveau \(l\). Cette dernière reconstruit les \(\mathbf{Y_i^{(l-1)}}\) qui ont permis le calcul des activations de la couche \(l\). Le processus est alors itéré jusqu’à atteindre la couche d’entrée \(l = 1\), les activations de la couche \(l\) étant alors rétroprojetées dans le plan image. La présence de couches d’agrégation et de rectification rend ce processus non inversible (par exemple, une couche d’agrégation maximum nécessite de connaître à quelles positions de l’image \(\mathbf{Y_i^{(l)}}\) sont situés les maxima retenus).

  • Faire passer un grand nombre d’images dans le réseau et, pour un neurone particulier, conserver celle qui a le plus activé ce neurone. Il est alors possible de visualiser les images pour comprendre ce à quoi le neurone s’intéresse dans son champ réceptif (Fig. 15).

_images/champr.png

Fig. 15 Champ récéptif de quelques neurones de la dernière couche d’agrégation du réseau AlexNet, superposées aux images ayant le plus fortement activé ces neurones. Le champ est encadré en blanc, et la valeur d’activation correspondante est reportée en haut. On voit par exemple que certains neurones sont très sensibles aux textes, d’autres aux réflexions spéculaires, ou encore aux hauts du corps (source :[4])#

  • Cacher (par un rectangle noir par exemple) différentes parties de l’image d’entrée qui est d’une certaine classe (disons un chien) et observer la sortie du réseau (la probabilité de la classe de l’image d’entrée). En représentant les valeurs de probabilité de la classe d’intérêt comme une fonction de la position du rectangle occultant, il est possible de voir si le réseau s’intéresse effectivement aux parties de l’image spécifiques de la classe, ou à des autres zones (le fond par exemple) (Fig. 16).

_images/occlusion.png

Fig. 16 Occlusion d’une image (à gauche). Le rectangle noir est déplacé dans l’image et pour chaque position la probabilité de la classe de l’image (ici un loulou de Poméranie) est enregistrée. Ces probabilités sont ensuite représentées sous forme d’une carte 2D (à droite). La probabilité de la classe s’effondre lorsque le rectangle couvre une partie de la face du chien. Cela suggère que cette face est grandement responsable de la forte probabilité de classement de l’image comme un loulou. A l’inverse, l’occlusion du fond n’altère pas la forte valeur de probabilité de la classe (source :[5])#

Méthodes fondées sur le gradient#

Pour comprendre quelle(s) partie(s) de l’image est (sont) utilisée(s) par le réseau pour effectuer une prédiction, il est possible de calculer des cartes de saillance (saliency maps). L’idée est relativement simple : calculer le gradient de la classe de sortie par rapport à l’image d’entrée. Cela indique à quel point une petite variation dans l’image induit un changement de prédiction. En visualisant les gradients, on observe alors par exemple leurs fortes valeurs, indiquant qu’une petite variation du pixel correspondant augmente la valeur de sortie.
Il est également possible d’utiliser le gradient par rapport à la dernière couche de convolution (approche Grad-CAM), ce qui permet de récupérer des informations de localisation spatiale des régions importantes pour la prédiction (Fig. 17 droite).

Plus généralement, en choisissant un neurone intermédiaire du réseau (d’une couche de convolution), la méthode de rétropropagation guidée calcule le gradient de sa valeur par rapport aux pixels de l’image d’entrée, ce qui permet de souligner les parties de l’image auxquelles ce neurone répond (Fig. 17 milieu).

_images/gradcam.png

Fig. 17 Approches par gradient de visualisation du fonctionnement d’un réseau convolutif. Comparaison de la méthode de rétropropagation guidée et de Grad-CAM (source :[6])#

Ces gradients peuvent également être utilisés dans la méthode de montée de gradient (gradient Ascent), dont l’objectif est de générer une image qui active de manière maximale un neurone donné du réseau. Le principe est d’itérativement passer l’image d’entrée \(\mathbf{I}\) dans le réseau pour obtenir les valeurs des cartes \(\mathbf{Y_i^{(l)}}\), de rétropropager pour obtenir le gradient d’un neurone par rapport aux pixels de \(\mathbf{I}\) et d’opérer une petite modification de ces pixels. Outre son aspect informatif sur la structure interne du réseau étudié (visualisation des cartes \(\mathbf{Y_i^{(l)}}\) intermédiaires), cette méthode produit des images parfois très artistiques (Fig. 18).

_images/monteeg.png

Fig. 18 Visualisation des 4 premières couches de convolution d’un réseau convolutif par montée de gradient (source :[7])#

Notons pour terminer que ce site propose une visualisation interactive du fonctionnement d’un réseau convolutif.

Implémentation#

import numpy as np
from matplotlib import pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torchsummary import summary
import torch.nn.functional as F
from torch.optim.lr_scheduler import StepLR

On travaille sur les données MNIST

# taille des batchs
train_batch_size=128
test_batch_size = 128

# Learning rate
lr = 0.001

# Nombre d'epochs 
num_epochs = 10

# Régularisation Dropout
dropout = 0.25

transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
        ])
dataset1 = datasets.MNIST('../data', train=True, download=True,
                       transform=transform)
dataset2 = datasets.MNIST('../data', train=False,
                       transform=transform)
train_kwargs = {'batch_size': train_batch_size}
test_kwargs = {'batch_size': test_batch_size}
train_loader = torch.utils.data.DataLoader(dataset1,**train_kwargs)
test_loader = torch.utils.data.DataLoader(dataset2, **test_kwargs)

et on implémente un réseau convolutif ayant l’architecture suivante :

CONV1 - RELU - MAX POOLING - CONV2 - RELU - MAX POOLING - FCL - DROPOUT - Prediction

avec :

  • des noyaux de convolution de taille 5\(\times\)5

  • un max pooling sur une région 2\(\times\)2

class CNN(nn.Module):
  def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(1, 32, 5, 1)
        self.conv2 = nn.Conv2d(32, 64, 5, 1)
        self.dropout = nn.Dropout(dropout)
        self.fc1 = nn.Linear(1024, 1024)
        self.fc2 = nn.Linear(1024, 10)

  def forward(self,x):
        x = self.conv1(x)
        x = F.relu(x)
        x = F.max_pool2d(x, 2)
        x = self.conv2(x)
        x = F.relu(x)
        x = F.max_pool2d(x, 2)
        x = torch.flatten(x, 1)
        x = self.fc1(x)
        x = F.relu(x)
        x = self.dropout(x)
        x = self.fc2(x)
        output = F.softmax(x, dim=1)
        return output

On créé ensuite les fonction pour entraîner et tester le réseau

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

def train(model, device, train_loader, optimizer, epoch):
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = F.nll_loss(output, target)
        loss.backward()
        optimizer.step()
        if batch_idx % 100 == 0:
            print('Epoch: {} [{}/{} ({:.0f}%)]\tPerte : {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item()))
    return loss


def test(model, device, test_loader):
    model.eval()
    test_loss = 0
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            output = model(data)
            test_loss += F.nll_loss(output, target, reduction='sum').item()  # sum up batch loss
            pred = output.argmax(dim=1, keepdim=True)  # get the index of the max log-probability
            correct += pred.eq(target.view_as(pred)).sum().item()

    test_loss /= len(test_loader.dataset)
    test_acc = 100. * correct / len(test_loader.dataset)

    print('\nPerte moyenne en test : {:.4f}, Précision : {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),test_acc
        ))
    return test_loss,test_acc

et on instantie le modèle

model = CNN().to(device)
summary(model, (1,28,28))

puis on l’entraîne

optimizer = optim.Adam(model.parameters(), lr=lr)

scheduler = StepLR(optimizer, step_size=1)
trainLoss = []
testLoss = []
testAcc = []
for epoch in range(1, num_epochs + 1):
    trainLoss.append(train(model, device, train_loader, optimizer, epoch).detach().numpy())
    t,a = test(model, device, test_loader)
    testLoss.append(t)
    testAcc.append(a)
    scheduler.step()
    
plt.plot(trainLoss, '-b',label='train')
plt.plot(testLoss, 'r',label='test')
plt.legend(loc='best')
plt.title("Fonction de perte")
plt.xlabel("epoch")
plt.ylabel("Perte")
plt.figure()
plt.plot(testAcc)
plt.xlabel("epoch")
plt.ylabel("Précision")
plt.title("Précision en test")
plt.tight_layout()
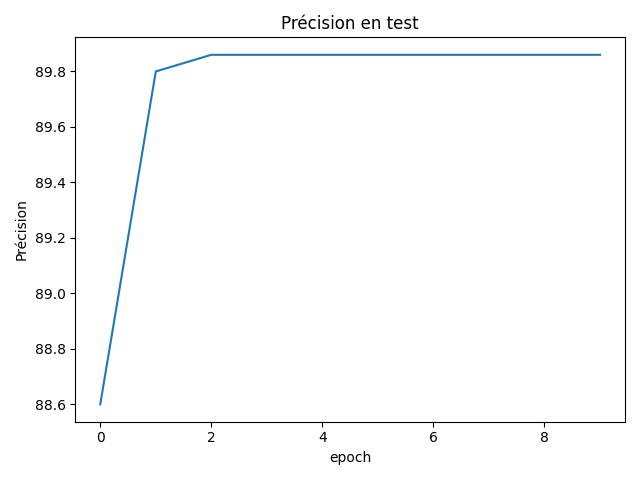
_images/precisionCNN.png

Fig. 19 Précision en apprentissage.#

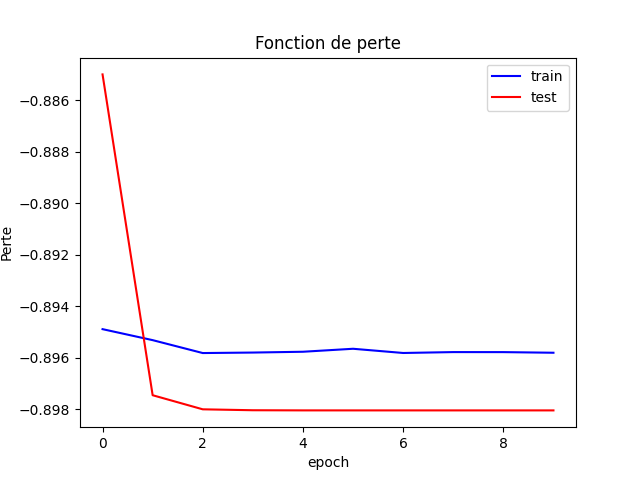
_images/perteCNN.png

Fig. 20 Fonction de perte.#

[1]

V. Nair and G. Hinton. Rectified linear units improve restricted boltzmann machines. In Johannes Fürnkranz and Thorsten Joachims, editors, ICML, 807–814. Omnipress, 2010. URL: http://dblp.uni-trier.de/db/conf/icml/icml2010.html#NairH10.

[2]

Xavier Glorot, Antoine Bordes, and Yoshua Bengio. Deep sparse rectifier neural networks. In Geoffrey J. Gordon, David B. Dunson, and Miroslav Dudík, editors, AISTATS, volume 15 of JMLR Proceedings, 315–323. JMLR.org, 2011. URL: http://dblp.uni-trier.de/db/journals/jmlr/jmlrp15.html#GlorotBB11.

[3]

Sergey Ioffe and Christian Szegedy. Batch normalization: accelerating deep network training by reducing internal covariate shift. In Francis R. Bach and David M. Blei, editors, ICML, volume 37 of JMLR Workshop and Conference Proceedings, 448–456. JMLR.org, 2015. URL: http://dblp.uni-trier.de/db/conf/icml/icml2015.html#IoffeS15.

[4]

R. Girshick, J. Donahue, T. Darrell, and J. Malik. Rich feature hierarchies for accurate object detection and semantic segmentation. In 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), volume 00, 580–587. June 2014. URL: https://ieeexplore.ieee.org/abstract/document/6909475/, doi:10.1109/CVPR.2014.81.

[5]

Matthew D. Zeiler and Rob Fergus. Visualizing and understanding convolutional networks. CoRR, 2013. URL: http://dblp.uni-trier.de/db/journals/corr/corr1311.html#ZeilerF13.

[6]

Ramprasaath R. Selvaraju, Michael Cogswell, Abhishek Das, Ramakrishna Vedantam, Devi Parikh, and Dhruv Batra. Grad-cam: visual explanations from deep networks via gradient-based localization. In ICCV, 618–626. IEEE Computer Society, 2017. URL: http://dblp.uni-trier.de/db/conf/iccv/iccv2017.html#SelvarajuCDVPB17.

[7]

Jason Yosinski, Jeff Clune, Anh Mai Nguyen, Thomas J. Fuchs, and Hod Lipson. Understanding neural networks through deep visualization. CoRR, 2015. URL: http://dblp.uni-trier.de/db/journals/corr/corr1506.html#YosinskiCNFL15.