Auto-encodeurs

Introduction

Un autoencodeur est algorithme entraîné de manière non supervisée à reproduire son entrée \(\mathbf{x}\in \mathcal{X}\). Il peut être vu (Fig. 21) comme composé de deux parties : un encodeur E qui transforme \(\mathbf{x}\) en un code déterministe \(\mathbf{h} = f(\mathbf{x} ; \mathbf{w_E})\in \mathcal{H}\) ou une distribution \(\textbf p_{encodeur} (\mathbf{h}|\mathbf{x},\mathbf{w_E})\), qui représente l’entrée ; et un décodeur D qui produit une reconstruction déterministe \(\mathbf{\hat{x}} = g(\mathbf{h} ; \mathbf{w_D})\) de \(\mathbf{x}\) ou une distribution \(\textbf p_{decodeur} (\mathbf{x}|\mathbf{h},\mathbf{w_D})\). Les vecteurs \(\mathbf{w_E}\) et \(\mathbf{w_D}\) sont les paramètres de E et D. Le plus souvent, l’encodeur et le décodeur sont des réseaux de neurones (perceptrons multicouches plus ou moins profonds, réseaux convolutifs ou récurrents,…) et les paramètres sont donc les poids de ces réseaux. À ce titre, l’entraînement peut être réalisé avec les mêmes algorithmes que ceux utilisés dans les réseaux de neurones classiques.
Entraîner un autoencodeur à reconstruire \(g\circ f(\mathbf{x})=\mathbf{x}\) pour tout \(\mathbf{x}\) n’est pas utile (on apprend l’identité). On contraint donc le réseau à ne pas reproduire parfaitement l’entrée, et à ne s’intéresser qu’à certains aspects de la reconstruction, ce qui lui permet d’apprendre des propriétés utilies des données.

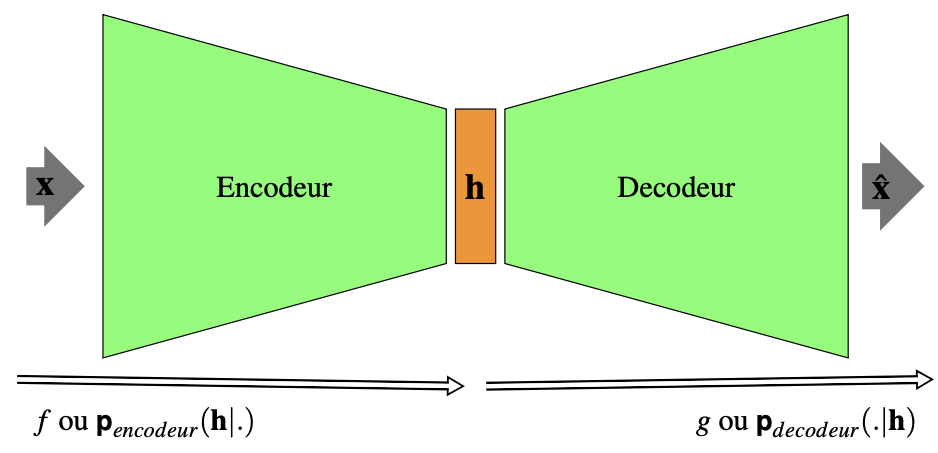
Fig. 21 Architecture générale d’un autoencodeur

Influence de la taille de l’espace de codage

Le cas \(|\mathcal{H}|<|\mathcal{X}|\)

Lorsque la dimension du code \(\mathbf{h}\) est inférieure à celle de \(\mathbf{x}\), l’encodeur E apprend à réduire la dimension. Le décodeur, une fois appris, permet de créer une donnée dans \(\mathcal{X}\) à partir d’un point de \(\mathcal{H}\) : il agit donc comme un modèle génératif.
L’apprentissage (la recherche des valeurs de \(\mathbf{w_E}\) et \(\mathbf{w_D}\)) s’effectue par minimisation d’une fonction de perte

\[\ell(\mathbf{x} , g\left [f(\mathbf{x} ; \mathbf{w_E}); \mathbf{w_D})\right ]\]

Si \(g\) est linéaire et \(\ell\) est la fonction de perte quadratique, alors l’autoencodeur agit comme l’analyse en composantes principales. Dans le cas plus général, l’autoencodeur apprend une représentation plus complexe des données. Il faut cependant prendre garde à ce que \(f\) et \(g\) ne soient pas trop complexes, auquel cas l’autoencodeur ne saura faire que copier exactement l’entrée, sans extraire dans \(\mathcal{H}\) d’information utile sur les données.

L’espace \(\mathcal{H}\) peut être utilisé pour de la visualisation en dimension réduite des données, pour des tâches de classification, ou plus simplement pour un espace de représentation plus compact des données de \(\mathcal{X}\) (Fig. 22).

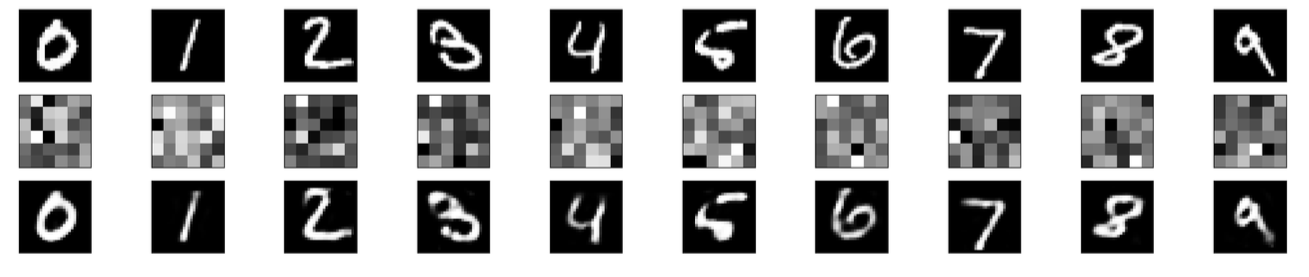
Fig. 22 Utilisation d’un autoencodeur pour la compression et la génération de chiffres manuscrits. Les images MNIST (28\(\times\)28, ligne du haut) sont encodées par un simple perceptron multicouche à activation sigmoïde et une seule couche cachée de taille 36. Le code est visualisé (ligne du milieu) sous la forme d’images 6\(\times\)6. Le décodeur produit des images reconstruites (ligne du bas) à partir de ce code

Le cas \(|\mathcal{H}|\geq|\mathcal{X}|\)

Si la taille de l’espace de représentation \(\mathcal{H}\) est supérieure à celle de l’espace d’entrée, on comprend assez facilement qu’il est très aisé pour l’autoencodeur d’apprendre l’identité, sans extraire d’information utile des données initiales (il suffit de propager \(\mathcal{X}\) dans \(\mathcal{H}\)). Il est donc nécessaire de contraindre le modèle.

Autoencodeurs régularisés

Régulariser un autoencodeur permet d’entraîner efficacement l’algorithme, en choisissant de plus la dimension de \(\mathcal H\) et la complexité de \(f\) et \(g\) en fonction de la complexité de la distribution à modéliser. Plutôt que de limiter la capacité du modèle (en imposant par exemple que E et D soient des réseaux multicouches à faible profondeur et/ou que \(\mathcal H\) soit de faible dimension), la régularisation construit une fonction de perte qui encourage l’autoencodeur à avoir des propriétés supplémentaires, en plus de celle de reproduire son entrée.

Un autoencodeur régularisé minimise la fonction

\[\ell(\mathbf{x} , g\left [f(\mathbf{x} ; \mathbf{w_E}); \mathbf{w_D})\right ] + \beta \Omega(\mathbf{h})\]

où \(\Omega(\mathbf{h})\) est un terme de pénalisation permettant de contraindre les paramètres du modèle et \(\beta\in\mathbb{R}\) contrôle le poids du terme de pénalité dans l’optimisation.

Autoencodeurs parcimonieux

Les autoencodeurs parcimonieux (ou épars) sont typiquement utilisés pour apprendre des caractéristiques pertinentes des données d’entrée, qui sont ensuite utilisées comme entrées d’algorithmes de classification ou de régression.

Supposons que E et D soient des perceptrons multicouches. Il est alors par exemple possible d’imposer aux neurones d’être « inactifs » la plupart du temps, en définissant l’inactivité comme une valeur de sortie du neurone proche de zéro (pour une sigmoïde, ou -1 pour une tangente hyperbolique). Pour cela, on dispose de \(m\) exemples \(\mathcal{S} = \{\mathbf{x_1}\cdots \mathbf{x_m}\}\). On note \(y^{(l)}_j(\mathbf{x})\) l’activation du neurone caché \(j\) de la couche \(l\) lorsque l’entrée \(\mathbf{x}\) est présentée au réseau. On note également

\[\hat\rho_j = \frac{1}{m} \sum_{i=1}^m \left[ y^{(l)}_j(\mathbf{x_i}) \right]\]

l’activation moyenne du neurone caché \(j\) sur présentation de \(\mathcal{S}\). L’objectif est alors d’imposer \(\hat\rho_j = \rho\), où \(\rho\) est une valeur proche de zéro (ainsi l’activation moyenne de chaque neurone caché doit être faible), par l’intermédiaire d’une définition adaptée de \(\Omega\). De nombreux choix sont possibles. Par exemple pour un réseau à une couche cachée :

\[\Omega(\mathbf{h}) = \displaystyle\sum_{j=1}^{n^{(2)}} \rho \log \frac{\rho}{\hat\rho_j} + (1-\rho) \log \frac{1-\rho}{1-\hat\rho_j} = \displaystyle\sum_{j=1}^{n^{(2)}} {KL}(\rho || \hat\rho_j),\]

où \({KL}(\rho || \hat\rho_j)\) est la divergence de Kullback-Leibler (KL) entre une variable aléatoire de loi de Bernoulli de moyenne \(\rho\) et une variable aléatoire de loi de Bernoulli de moyenne \(\hat\rho_j\).
On peut alors montrer que \({KL}(\rho || \hat\rho_j) = 0\) si \(\hat\rho_j = \rho\), et \({KL}\) croît de façon monotone lorsque \(\hat\rho_j\) s’éloigne de \(\rho\).

Le calcul des dérivées partielles et la descente de gradient changent peu pour l’algorithme d’optimisation. Il faut cependant connaître au préalable les \(\textstyle \hat\rho_j\) et donc faire dans un premier temps une propagation avant sur tous les exemples de \(\mathcal{S}\) permettant de calculer les activations moyennes.
Dans le cas où la base d’apprentissage est suffisamment petite, elle tient entièrement en mémoire et les activations peuvent être stockées pour calculer \(\textstyle \hat\rho_j\). Les activations stockées peuvent alors être utilisées dans l’étape de rétropropagation sur l’ensemble des exemples.
Dans le cas contraire, le calcul de \(\textstyle \hat\rho_j\) peut être fait en accumulant les activations calculées exemple par exemple, mais sans sauvegarder les valeurs de ces activations. Une seconde propagation sur chaque exemple sera alors nécessaire pour permettre la rétropropagation.

Les autoencodeurs parcimonieux peuvent également être vus d’un point de vue probabiliste comme des algorithmes maximisant la vraisemblance maximale d’un modèle génératif à variables latentes \(\mathbf{h}\). Supposons disposer d’une distribution jointe explicite

\[\textbf{p}_{modele}(\mathbf{x},\mathbf{h}) = \textbf{p}_{modele}( \mathbf{h})\textbf{p}_{modele}(\mathbf{x}|\mathbf{h})\]

La log vraisemblance peut alors s’écrire

\[log(\textbf{p}_{modele}(\mathbf{x})) = log \left (\displaystyle\sum_{\mathbf{h}} \textbf{p}_{modele}(\mathbf{x},\mathbf{h})\right )\]

L’autoencodeur approche cette somme juste pour une une valeur de \(\mathbf{h}\) fortement probable. Pour cette valeur, on maximise alors $\(log(\textbf{p}_{modele}(\mathbf{x},\mathbf{h})) = log(\textbf{p}_{modele}(\mathbf{h})) + log(\textbf{p}_{modele}(\mathbf{x}|\mathbf{h}))\)\( et \)log(\textbf{p}_{modele}(\mathbf{h}))$ peut être utilisée pour introduire de la parcimonie.

Par exemple si \(\textbf{p}_{modele}(h_i) = \frac{\lambda}{2} e^{-\beta|h_i| }\) (Laplace prior), alors

\[-log(\textbf{p}_{modele}(\mathbf{h})) = \displaystyle\sum_{i=1}^{|\mathcal{H}|}\left (\lambda |h_i| -log\frac{\lambda}{2} \right) = \Omega(\mathbf{h}) + c\]

et l’on retrouve une régularisation \(\ell_1\) (méthode Lasso).

Autoencodeurs contractifs

Une autre stratégie de régularisation consiste à faire dépendre \(\Omega\) du gradient du code en fonction des entrées :

\[\Omega(\mathbf{x},\mathbf{h}) = \displaystyle\sum_{i=1}^{|\mathcal{H}|}\|\nabla_{\mathbf{x}} h_i\|^2 =\left \|\frac{\partial f(\mathbf{x},\mathbf{w_E})}{\partial \mathbf{x}}\right \|_F^2\]

où \(\|.\|_F\) est la norme de Frobenius. Le modèle apprend alors une fonction qui change peu lorsque \(\mathbf{x}\) varie peu. Puisque la pénalité n’est appliquée que sur les exemples de \(\mathcal{S}\), les informations capturées dans le code concernent la distribution des données d’entraînement, et plus précisément la variété sur laquelle vivent les données de \(\mathcal{S}\). En ce sens, ces autoencodeurs sont à rapprocher des méthodes de Manifold Learning.

Autoencodeurs de débruitage

Plutôt que d’ajouter un terme à la fonction de perte, on peut directement changer cette dernière pour apprendre des caractéristiques utiles des données.
Un autoencodeur de débruitage considère la fonction de perte

\[\ell(\mathbf{x} , g\left [f(\mathbf{\tilde{x}} ; \mathbf{w_E}); \mathbf{w_D})\right ]\]

où \(\mathbf{\tilde{x}}\) est une version de \(\mathbf{{x}}\) bruitée par une distribution conditionnelle \(C(\mathbf{\tilde{x}},\mathbf{x})\). L’autoencodeur apprend alors une distribution de reconstruction \(\textbf{p}_R(\mathbf{x}\mid \mathbf{\tilde{x}})\) selon l”Algorithm 7 (Fig. 23).

Algorithm 7 (Algorithe d’apprentissage d’un autoencodeur de débruitage)

Entrée : \(\mathcal{S}\), \(C(\mathbf{\tilde{x}},\mathbf{x})\), un autoencodeur \((f,g)\)

Sortie : Un autoencodeur de débruitage

1. Tant que (non stop)

   1. Tirer un exemple \(\mathbf x\) de \(\mathcal{S}\)

   2. Tirer \(\mathbf {\tilde{x}}\) selon \(C(\mathbf{\tilde{x}},\mathbf{x})\)

   3. Estimer \(\textbf{p}_R(\mathbf{x}\mid \mathbf{\tilde{x}}) = \textbf{p}_{decodeur}(\mathbf{x}\mid \mathbf{h},\mathbf{w_D})=g(\mathbf{h},\mathbf{w_D})\) où \(\mathbf{h} = f(\mathbf{\tilde{x}},\mathbf{w_E})\)

L’apprentissage peut être vu comme une descente de gradient stochastique de

\[-\mathbb{E}_{\mathbf{x}\sim \textbf{p}_{\mathcal{S}}(\mathbf{x})} \mathbb{E}_{\mathbf{\tilde{x}}\sim C(\mathbf{\tilde{x}},\mathbf{x})} \left (log\;\textbf{p}_{decodeur} (\mathbf{x}|\mathbf{h}=f(\mathbf{\tilde{x}},\mathbf{w_E}),\mathbf{w_D})\right )\]

Fig. 23 Autoencodeur de débruitage sur les données MNIST. Les images \(\mathbf{x}\) (ligne du haut) sont corrompues par un bruit gaussien centré de variance unité (deuxième ligne). Un autoencodeur de débruitage est ensuite entraîné. Le code \(\mathbf{h}\) de taille 32 est visualisé (troisième ligne) sous la forme d’images 8\(\times\)4. Le décodeur produit les images débruitées de la dernière ligne.

Autoencodeurs variationnels

Le dernier modèle d’autoencodeurs que nous abordons sera traité plus précisément dans un chapitre dédié, dans la partie consacrée aux modèles génératifs.

Les autoencodeurs variationnels (VAE) [1] sont des modèles génératifs. Ce ne sont pas à proprement parler des autoencodeurs tels que nous les avons abordés dans les paragraphes précédents, ils empruntent juste une architecture similaire (Fig. 24), d’où leur nom.

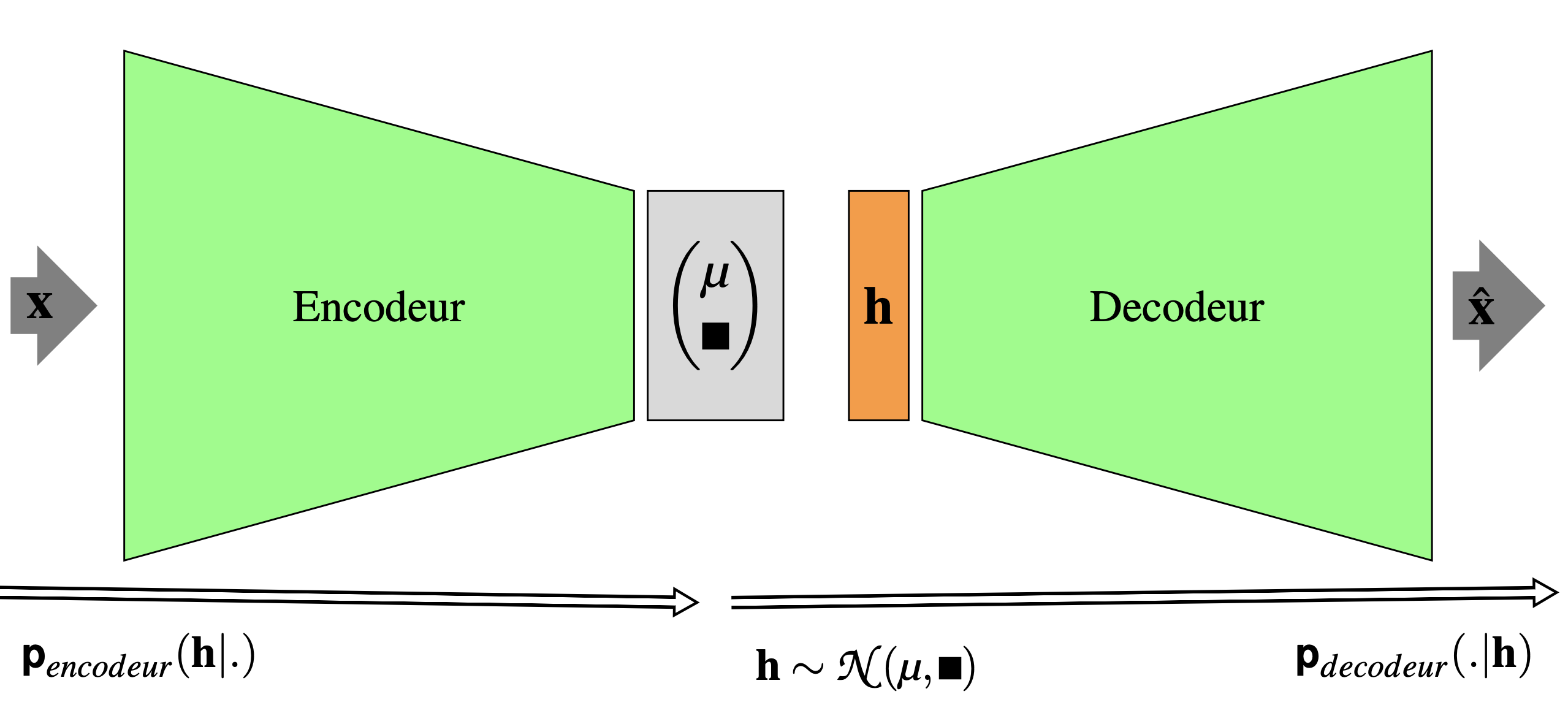
Fig. 24 Architecture générale d’un autoencodeur variationnel.

Au lieu d’apprendre \(f(.,\mathbf{w_E})\) et \(g(.,\mathbf{w_D})\), un autoencodeur variationnel apprend des distributions de probabilité \(\textbf{p}_{encodeur} (\mathbf{h}|\mathbf{x},\mathbf{w_E})\) et \(\textbf{p}_{decodeur} (\mathbf{x}|\mathbf{h},\mathbf{w_D})\).
Apprendre des distributions plutôt que des fonctions déterministes présente plusieurs avantages, et notamment :

• les données d’entrée peuvent être bruitées, et un modèle de distribution \(\textbf{p}_\mathbf{x}\) peut être plus utile

• il est possible d’utiliser \(\textbf{p}_{decodeur} (\mathbf{x}|\mathbf{h},\mathbf{w_D})\) pour échantillonner \(\mathbf{h}\) puis \(\mathbf{x}\), et donc de générer des données ayant des statistiques similaires aux éléments de \(\mathcal{S}\) (Fig. 25).

Abordons ces autoencodeurs sous l’angle des modèles génératifs. Supposons que nous voulions générer des points suivant la distribution \(\textbf{p}_\mathbf{x}\). Plutôt que d’inférer directement sur cette distribution, nous pouvons utiliser des variables latentes (le code des autoencodeurs). Les modèles à variables latentes font l’hypothèse que les données \(\mathbf{x}\) sont issues d’une variable non observée \(\mathbf{h}\). S’il peut être difficile de modéliser directement \(\textbf{p}_\mathbf{x}\), il peut être plus facile de choisira priori une distribution \(\textbf{p}_\mathbf{h}\) et chercher à modéliser \(\textbf{p}_{\mathbf{x}|\mathbf{h}}\).
Pour générer \(\mathbf{x}\sim \textbf{p}_\mathbf{x}\), un autoencodeur variationnel tire donc tout d’abord \(\mathbf{h}\sim \textbf{p}_\mathbf{h}\). \(\mathbf{h}\) est ensuite passé à un réseau de neurones et \(\mathbf{x}\) est finalement tiré selon \(\textbf{p}_{decodeur} (\mathbf{x}|\mathbf{h},\mathbf{w_D})\). L’entraînement est réalisé en maximisant la borne inférieure variationnelle :

\[\mathcal{L}(q) = \mathbb{E}_{\mathbf{h}\sim q(\mathbf{h}|\mathbf{x})} log \left (\textbf{p}_{decodeur} (\mathbf{x}|\mathbf{h},\mathbf{w_D})\right ) -KL\left (q(\mathbf{h}|\mathbf{x}) ||\textbf{p}_\mathbf{h}\right )\]

où \(KL\) est la divergence de Kullback Leibler déjà rencontrée dans les autoencodeurs parcimonieux. Le premier terme de \(\mathcal{L}(q)\) est la log vraisemblance de la reconstruction trouvée dans les autoencodeurs classiques, tandis que le second terme tend à rapprocher la distribution a posteriori \(q(\mathbf{h}|\mathbf{x})\) et le modèle a priori \(\textbf{p}_\mathbf{h}\). Dans les techniques classiques d’inférence, \(q\) est approché par optimisation. Dans les autoencodeurs variationnels, on entraîne un encodeur paramétrique (un réseau de neurones paramétré par \(\mathbf{w_E}\)) qui produit les paramètres de \(q\). Tant que \(\mathbf{h}\) est continue, il est donc possible de rétropropager à travers les tirages de \(\mathbf{h}\) effectués selon \(q(\mathbf{h}|\mathbf{x}) = q(\mathbf{h}| f(\mathbf{x} ; \mathbf{w_E}))\) pour obtenir le gradient par rapport à \(\mathbf{w_E}\). L’apprentissage consiste alors simplement à maximiser \(\mathcal{L}\) par rapport à \((\mathbf{w_E},\mathbf{w_D})\).

Il est courant de choisir comme prior \(\textbf{p}_\mathbf{h}\) une loi normale centrée réduite \(\mathcal{N}(\mathbf{0},\mathbf{I})\). Cette simplicité apparente ne réduit pas le pouvoir d’expression du modèle si l’effort est fait sur l’optimisation de la distribution \(\textbf{p}_{decodeur} (\mathbf{x}|\mathbf{h},\mathbf{w_D})\). L’encodeur E est alors un réseau de neurones générant des paramètres de distribution de \(q\) dans \(\mathcal{H}\), soit un vecteur de moyenne \(\mu\) et une matrice de covariance \(\mathbf{\Sigma}\).
Notons enfin que la rétropropagation du gradient nécessite une astuce de calcul dans \(\mathcal{H}\), dite astuce de reparamétrisation : la génération de \(\mathbf{h}\sim \textbf{p}_{encodeur} (\mathbf{h}|\mathbf{x},\mathbf{w_E})\) se fait effectivement en tirant une variable aléatoire \(\epsilon\sim\mathcal{N}(\mathbf{0},\mathbf{I})\), puis en calculant \(\mathbf{h}\)=\(\mu\) + \(\Sigma^{1/2} \epsilon\). L’échantillonnage se fait alors seulement pour \(\epsilon\), qui n’a pas besoin d’être rétropropagé.

Fig. 25 Visualisation de l’espace latent \(\mathcal H = \mathbb{R}^2\) appris par un autoencodeur variationnel sur les donneés MNIST. Pour chaque valeur \(\mathbf h_i\) discrétisée sur \(\mathcal H\) est affichée une image \(\mathbf x ∼ \textbf{p}_{decodeur}(\mathbf{x}\mid \mathbf h_i,\mathbf{w_D})\). Les chiffres de la même classe sont groupés dans cet espace, et les axes de \(\mathcal H\) ont une interprétation (l’axe horizontal semble souligner le caractère « penché » des chiffres).

Implémentation

import numpy as np
from matplotlib import pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torchvision.utils import make_grid

On travaille sur les données MNIST

# taille des batchs
train_batch_size=128
test_batch_size = 128

# Paramètres du réseau et de l'apprentissage
lr = 0.001
num_epochs = 100
num_hidden_1 = 256  
num_hidden_2 = 128  
num_input = 784  

transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
        ])
dataset1 = datasets.MNIST('../data', train=True, download=True,
                       transform=transform)
dataset2 = datasets.MNIST('../data', train=False,
                       transform=transform)
train_kwargs = {'batch_size': train_batch_size}
test_kwargs = {'batch_size': test_batch_size}
train_loader = torch.utils.data.DataLoader(dataset1,**train_kwargs)
test_loader = torch.utils.data.DataLoader(dataset2, **test_kwargs)

et on implémente un autoencodeur :

class AE(nn.Module):
    def __init__(self, x_dim, h_dim1, h_dim2):
        super(AE, self).__init__()
        # encodeur 
        self.fc1 = nn.Linear(x_dim, h_dim1)
        self.fc2 = nn.Linear(h_dim1, h_dim2)
        # decodeur part
        self.fc3 = nn.Linear(h_dim2, h_dim1)
        self.fc4 = nn.Linear(h_dim1, x_dim)

    def encodeur(self, x):
        x = torch.sigmoid(self.fc1(x))
        x = torch.sigmoid(self.fc2(x))
        return x

    def decodeur(self, x):
        x = torch.sigmoid(self.fc3(x))
        x = torch.sigmoid(self.fc4(x))
        return x

    def forward(self, x):
        x = self.encodeur(x)
        x = self.decodeur(x)
        return x

On instantie le modèle

model = AE(num_input, num_hidden_1, num_hidden_2)
optimizer = optim.Adam(model.parameters())
loss_function = nn.MSELoss()

Et on entraîne

for i in range(num_epochs):
    train_loss = 0
    for batch_idx, (data, _) in enumerate(train_loader):
        inputs = torch.reshape(data,(-1, 784)) 
        optimizer.zero_grad()
        recons = model(inputs)
        loss = loss_function(recons, inputs)
        loss.backward()
        train_loss += loss.item()
        optimizer.step()
        
    if i%10==0:    
        print('Epoch: {} perte moyenne: {:.9f}'.format(i, train_loss))

La figure (Fig. 26) montre l’évolution de la reconstruction au cours des itérations.

Fig. 26 Reconstruction aux itérations 0,10,20,30 et 40 d’un sous-ensemble de l’ensemble d’apprentissage.

Pour finalement visualiser les résultats de la reconstruction sur un ensemble de test (Fig. 27).

def imshow(img):
    npimg = img.numpy()
    ax = plt.gca()
    plt.imshow(np.transpose(npimg, (1, 2, 0))) 
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
    plt.tight_layout()

inputs, _ = next(iter(test_loader))
inputs_example = make_grid(inputs[:16,:,:,:],4)
inputs=torch.reshape(inputs,(-1,784))

outputs=model(inputs)
outputs=torch.reshape(outputs,(-1,1,28,28))
outputs=outputs.detach().cpu()
outputs_example = make_grid(outputs[:16,:,:,:],4)

fig = plt.figure(122)
fig.add_subplot(121)
fig.set_title("Images originales")
imshow(inputs_example)
fig.add_subplot(122)
fig.set_title("Images reconstruites")
imshow(outputs_example)

Fig. 27 Images originales de test (gauche) et reconstruites (droite) par l’autoencodeur.

L’Autoencodeur peut ensuite être utilisé par exemple en reconnaissance de chiffres. Une manière simple consiste à choisir au hasard 10 échantillons d’apprentissage de chaque classe et à leur attribuer une étiquette. Ensuite, étant donné les données de test, il est possible de prédire à quelles classes elles appartiennent en trouvant les échantillons d’apprentissage étiquetés les plus similaires dans l’espace latent \(\mathcal H\).

# Données d'entraînement
x_train, y_train = next(iter(train_loader))
candidates = np.random.choice(train_batch_size, 10*10)
x_train = x_train[candidates]
y_train = y_train[candidates]

# Données test à étiqueter
x_test, y_test = next(iter(test_loader))
candidates = np.random.choice(test_batch_size, 10*10)
x_test = x_test[candidates_test]
y_test = y_test[candidates]

#Représentation des données dans l'espace latent
h_train=model.encodeur(torch.reshape(x_train,(-1,784)))
h_test=model.encodeur(torch.reshape(x_test,(-1,784)))

# Données d'entraînement les plus proches (MSE) de chaque exemple de test
MSEs = np.mean(np.power(np.expand_dims(h_test.detach().cpu(), axis=1) - np.expand_dims(h_train.detach().cpu(), axis=0), 2), axis=2)
neighbours = MSEs.argmin(axis=1)
predicts = y_train[neighbours]

print("Taux de reconnaissance des chiffres manuscrits sur l'ensemble de test :  %.1f%%" % (100 * (y_test == predicts).numpy().astype(np.float32).mean()))

[1]

D. Kingma and M. Welling. Auto-encoding variational bayes. CoRR, 2013. URL: http://dblp.uni-trier.de/db/journals/corr/corr1312.html#KingmaW13.