Réseaux antagonistes générateurs

Principe

Dans les réseaux antagonistes génératifs (GAN: Generative Adversarial Networks [1]), la tâche d’apprentissage d’un modèle génératif est exprimée comme un jeu à somme nulle à deux joueurs entre deux réseaux, le générateur \(G\) et le discriminateur \(D\) (Fig. 68).

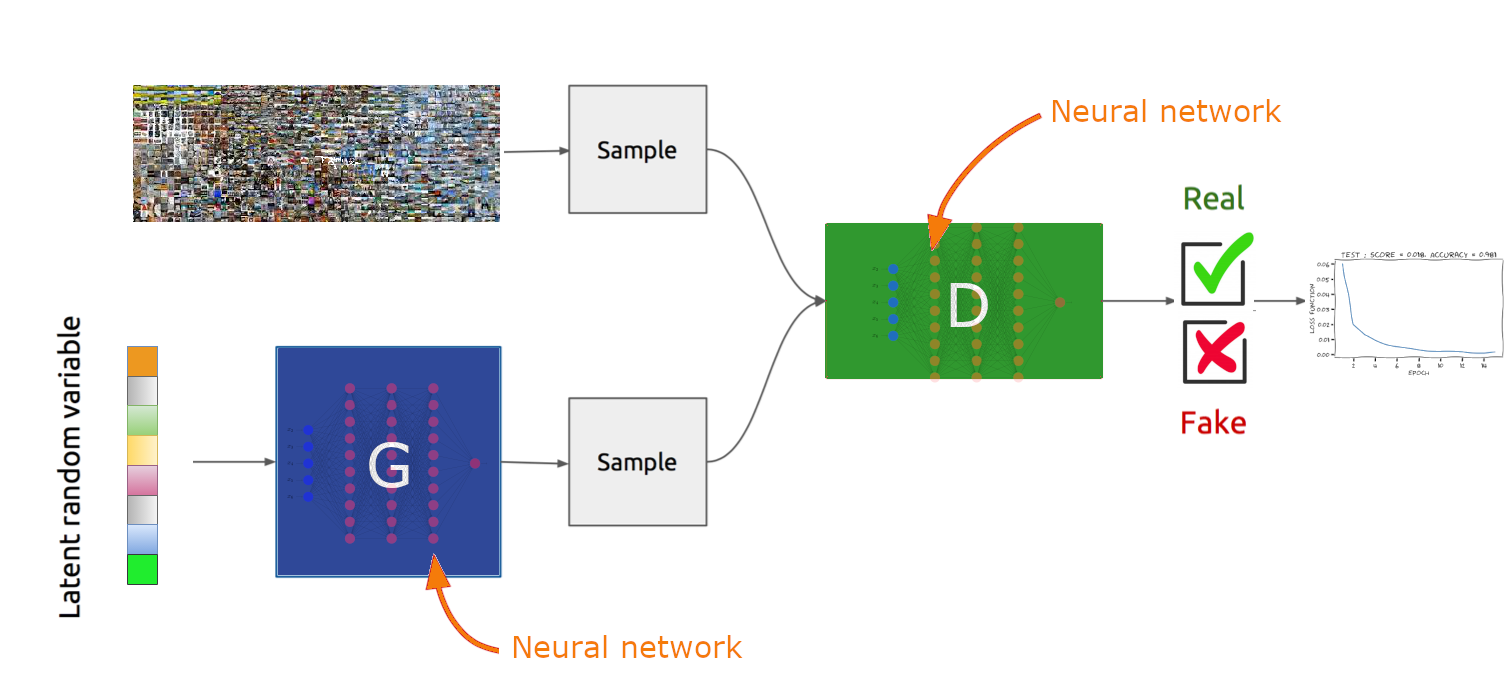
Fig. 68 Architecture globale d’un GAN

Le générateur \(G=G(.,\boldsymbol\theta): \mathcal Z\rightarrow \mathcal X\) met en correspondance un espace latent équipé d’une distribution \(p(z)\) avec l’espace des données, induisant ainsi une distribution

\[x\sim q(x,\boldsymbol\theta) \Leftrightarrow z\sim p(z), x=G(z,\boldsymbol\theta)\]

Le discriminateur \(D=D(.,\boldsymbol\phi): \mathcal X\rightarrow [0,1]\) est un classifieur entraîné pour distinguer les vrais exemples \(x\sim p(x)\) des exemples générés par \(G\) \(x\sim q(x,\boldsymbol\theta)\)

Pour un \(G\) fixé, \(D\) peut-être entraîné en construisant un ensemble d’apprentissage

\[\mathcal E_a = \{(x_i,1),i\in[\![1,N]\!],(G(z_i,\boldsymbol\theta),0),i\in[\![1,N]\!]\}\]

où \(x_i\sim p(x)\) et \(z_i\sim p(z)\), et en minimisant l’entropie croisée binaire

\[\begin{split}\begin{align} \mathcal L(\boldsymbol\phi)&=& -\frac{1}{2N}\displaystyle\sum_{i=1}^N \left [log D(x_i,\boldsymbol \phi)+ log (1-D(G(z_i,\boldsymbol\theta),\boldsymbol\phi))\right ]\\ &\approx& -\mathbb{E}_{x\sim p(x)}[log D(x_i,\boldsymbol \phi)] - \mathbb{E}_{z\sim p(z)}log (1-D(G(z_i,\boldsymbol\theta),\boldsymbol\phi)) \end{align} \end{split}\]

Cependant, la situation est légèrement plus complexe puisque \(G\) doit également être entraîné pour tromper \(D\). Heureusement, cela revient à maximiser la perte de \(D\).

Soit

\[f(\boldsymbol\theta,\boldsymbol\phi) = \mathbb{E}_{x\sim p(x)}[log D(x_i,\boldsymbol \phi)] + \mathbb{E}_{z\sim p(z)}log (1-D(G(z_i,\boldsymbol\theta),\boldsymbol\phi))\]

Alors :

• pour \(G\) fixé \(f(\boldsymbol\theta,\boldsymbol\phi)\) est élevée si \(D\) discrimine les vrais exemples des faux

• si \(\hat D\) est le meilleur classifieur étnt donné \(G\), et si \(f(\boldsymbol\theta,\boldsymbol\phi)\) est élevée, alors \(G\) n’arrive pas à reproduire la distribution des données \(p(x)\)

• Inversement, \(G\) est un bon modèle génératif, capable de reproduire \(p(x)\), si \(f(\boldsymbol\theta,\boldsymbol\phi)\) est faible lorsque \(\hat D\) est le meilleur classifieur.

Tout ceci implique que l’on recherche \(G=G(.,\boldsymbol\theta^*)\) tel que

\[\boldsymbol\theta^* = Arg\; min_{\boldsymbol\theta}\;max_{\boldsymbol\phi}f(\boldsymbol\theta,\boldsymbol\phi)\]

En pratique, ce problème d’optimisation minimax est approché par une descente de gradient par batch alternée :

1. \(\boldsymbol\phi = \boldsymbol\phi+\eta\nabla_{\boldsymbol\phi}f(\boldsymbol\theta,\boldsymbol\phi)\) (Fig. 69)

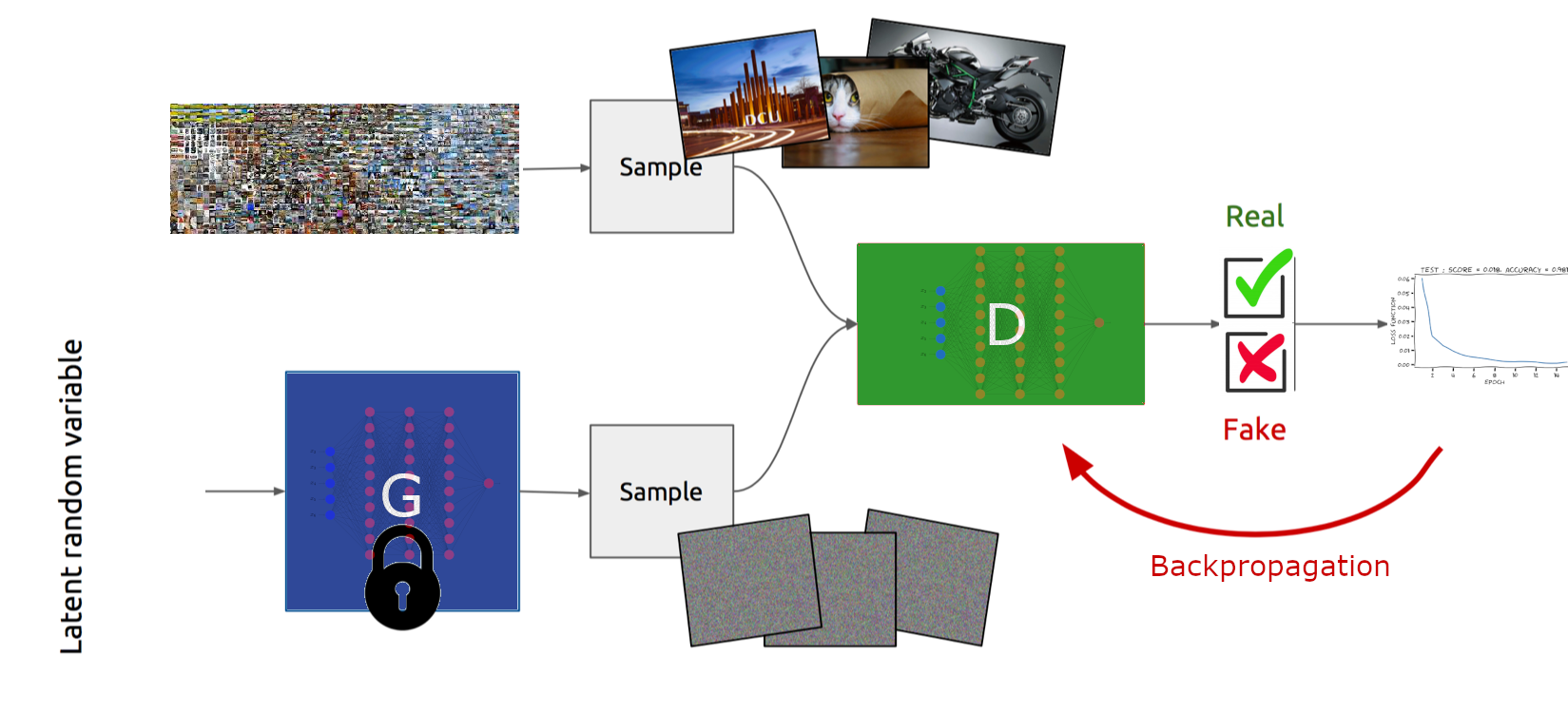
Fig. 69 Optimisation des paramètres de \(D\), à \(G\) fixé

2. \(\boldsymbol\theta = \boldsymbol\theta-\eta\nabla_{\boldsymbol\theta}f(\boldsymbol\theta,\boldsymbol\phi)\) (Fig. 70)

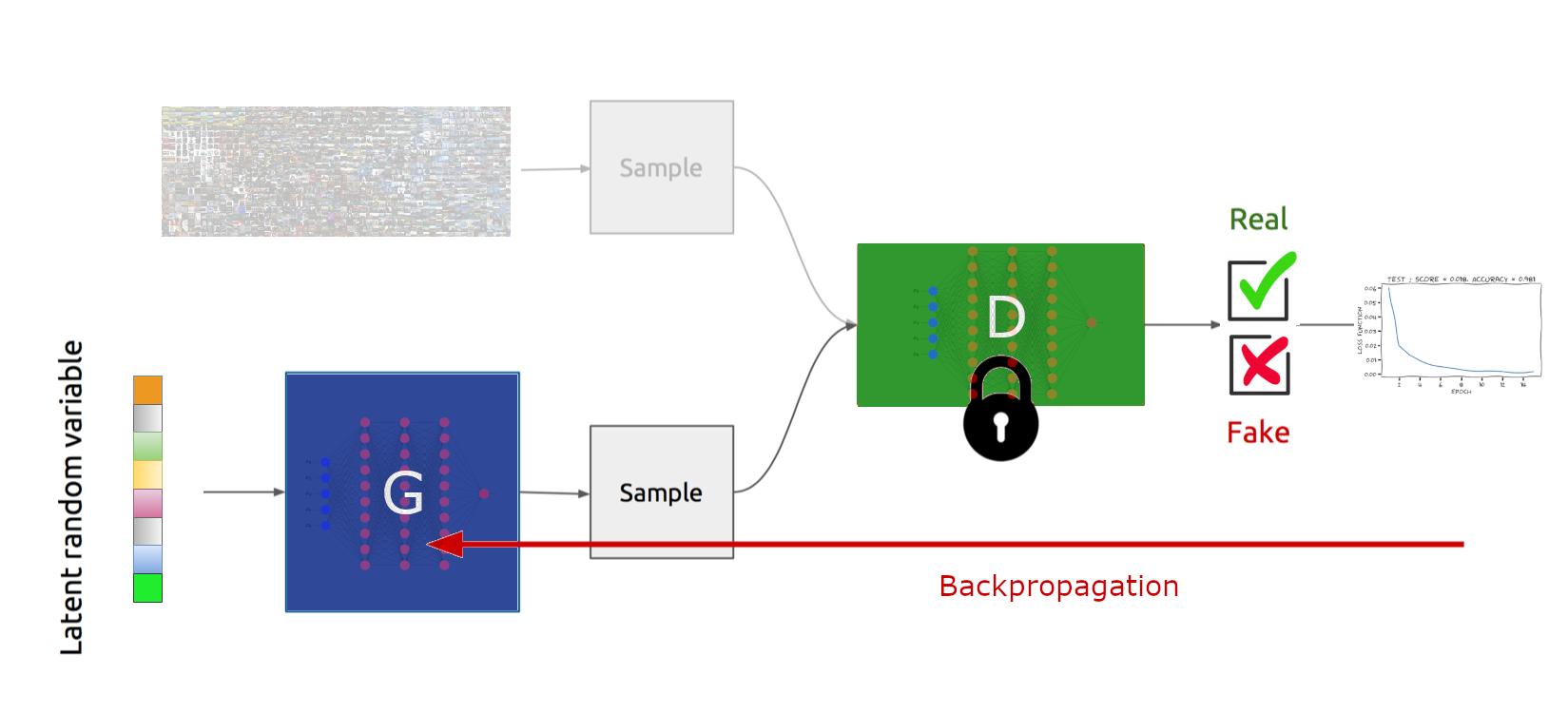
Fig. 70 Optimisation des paramètres de \(G\), à \(D\) fixé

Goodfellow propose dans [1] une illustration du processus d’apprentissage d’un GAN (Fig. 71). Dans cette figure, on illustre de gauche à droite un modèle à l’état initial, l’évolution après la mise à jour de \(D\), puis de \(G\), et enfin l’état à convergence. La courbe en points noir est la distribution des données \(p(x)\), la courbe verte la distribution \(p(z)\) de \(G\), la courbe bleue pointillée la sortie de \(D\). Les \(z\in\mathcal Z\) sont tirés uniformément (partie inférieure des graphiques)

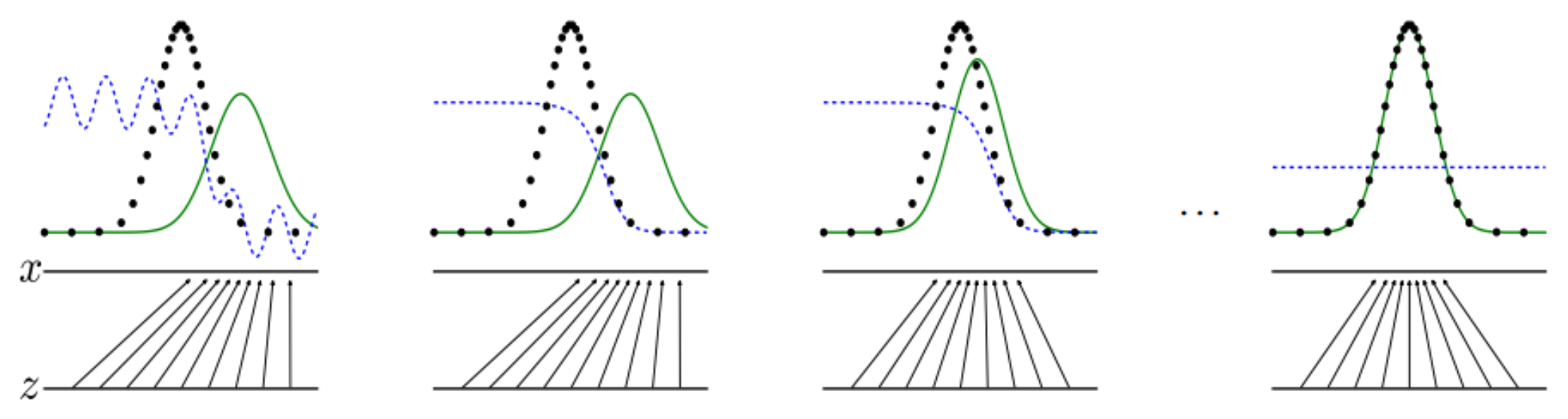
Fig. 71 Processus d’apprentissage d’un GAN.

Analyse

A \(G\) fixé (donc \(\boldsymbol\theta\) fixé), le classifieur \(D\) de paramètres optimaux \(\boldsymbol\phi_{\boldsymbol\theta}^*\) est optimal si et seulement si

\[\forall x, D(x,\boldsymbol\phi_{\boldsymbol\theta}^*) = \frac{p(x)}{p(x)+q(x;\boldsymbol\theta)}\]

En notant \(KL(p||q)\) la divergence de Kullback-Leibler entre \(p\) et \(q\) et \(JSD\) la divergence de Jensen-Shannon, on a ainsi :

\[\begin{split} \begin{aligned} & \min _\boldsymbol\theta \max _\boldsymbol\phi f(\boldsymbol\theta,\boldsymbol\phi)=\min _\boldsymbol\theta f(\boldsymbol\theta,\boldsymbol\phi_{\boldsymbol\theta}^*) \\ & =\min _\boldsymbol\theta \mathbb{E}_{x \sim p(x)}\left[\log \frac{p(x)}{q(x, \boldsymbol\theta)+p(x)}\right]+\mathbb{E}_{x \sim q(x ; \theta)}\left[\log \frac{q(x ; \boldsymbol\theta)}{q(x ; \boldsymbol\theta)+p(x)}\right] \\ & =\min _\boldsymbol\theta \mathrm{KL}\left(p(x) \| \frac{p(x)+q(x ; \boldsymbol\theta)}{2}\right) +\mathrm{KL}\left(q(x ; \boldsymbol\theta) \| \frac{p(x)+q(x ; \boldsymbol\theta)}{2}\right)-\log 4 \\ & =\min _\boldsymbol\theta 2 \mathrm{JSD}(p(x) \| q(x ; \boldsymbol\theta))-\log 4 \end{aligned} \end{split}\]

Remark 2

La divergence de Kullback-Leibler est une mesure de dissimilarité entre deux distributions de probabilités. Pour deux distributions \(p\) et \(q\), elle est définie par

\[KL(p\|q) = \sum_{x \in X} p(x) \log \frac{p(x)}{q(x)}\]

La divergence de Jensen-Shannon est une autre méthode de mesure de la similarité entre deux distributions de probabilité, définie par

\[JSD(p,q)=\frac12 (KL(p\|m) + KL(q\|m))\quad\textrm{avec }m = \frac12(p+q)\]

Ainsi

\[\boldsymbol\theta^* = Arg\; min_{\boldsymbol\theta}\;max_{\boldsymbol\phi}f(\boldsymbol\theta,\boldsymbol\phi) = Arg\; min_{\boldsymbol\theta}\; \mathrm{JSD}(p(x) \| q(x ; \boldsymbol\theta))\]

Puisque \(\mathrm{JSD}(p(x) \| q(x ; \boldsymbol\theta))\) est minimum si et seulement si \(\forall x, p(x) = q(x ; \boldsymbol\theta)\), alors la solution du problème minimax correspond à un modèle génératif qui reproduit la distribution des données d’entrée.

Problèmes

L’entraînement d’un tel GAN, formulé de manière standard, pose des comportements pathologiques :

• Oscillations sans convergence : contrairement à la minimisation de perte standard, la descente de gradient stochastique alternée n’a aucune garantie de convergence.

• Gradients disparus (vanishing gradients) : lorsque le classificateur \(D\) est trop bon, la fonction \(f\) sature et les gradients deviennent nuls, empêchant \(G\) de se mettre à jour.

• Effondrement des modes (mode collapsing) : le générateur \(G\) modélise très bien une petite sous-population, en se concentrant sur quelques modes de la distribution des données : lorsque \(G\) est entraîné à \(D\) fixé, il produit un mode \(x^*\) qui trompe au mieux \(D\). Lorsque \(D\) est entraîné, la meilleure manière pour lui de détecter des données générées par \(G\) est de se concentrer sur ce mode \(x^*\). Ainsi \(G\) est encouragé à ne produire que \(x^*\) (Fig. 72).

Fig. 72 Mode collapsing (source :[2])

Des solutions existent pour chacun de ces problèmes, mais ne sont pas abordées dans ce cours. On trouvera ici des modèles de GAN répondant à ces problématiques, ainsi que de nombreux autres.

Quelques exemples

Apprentissage d’une fonction de \(\mathbb{R}\rightarrow \mathbb{R}\)

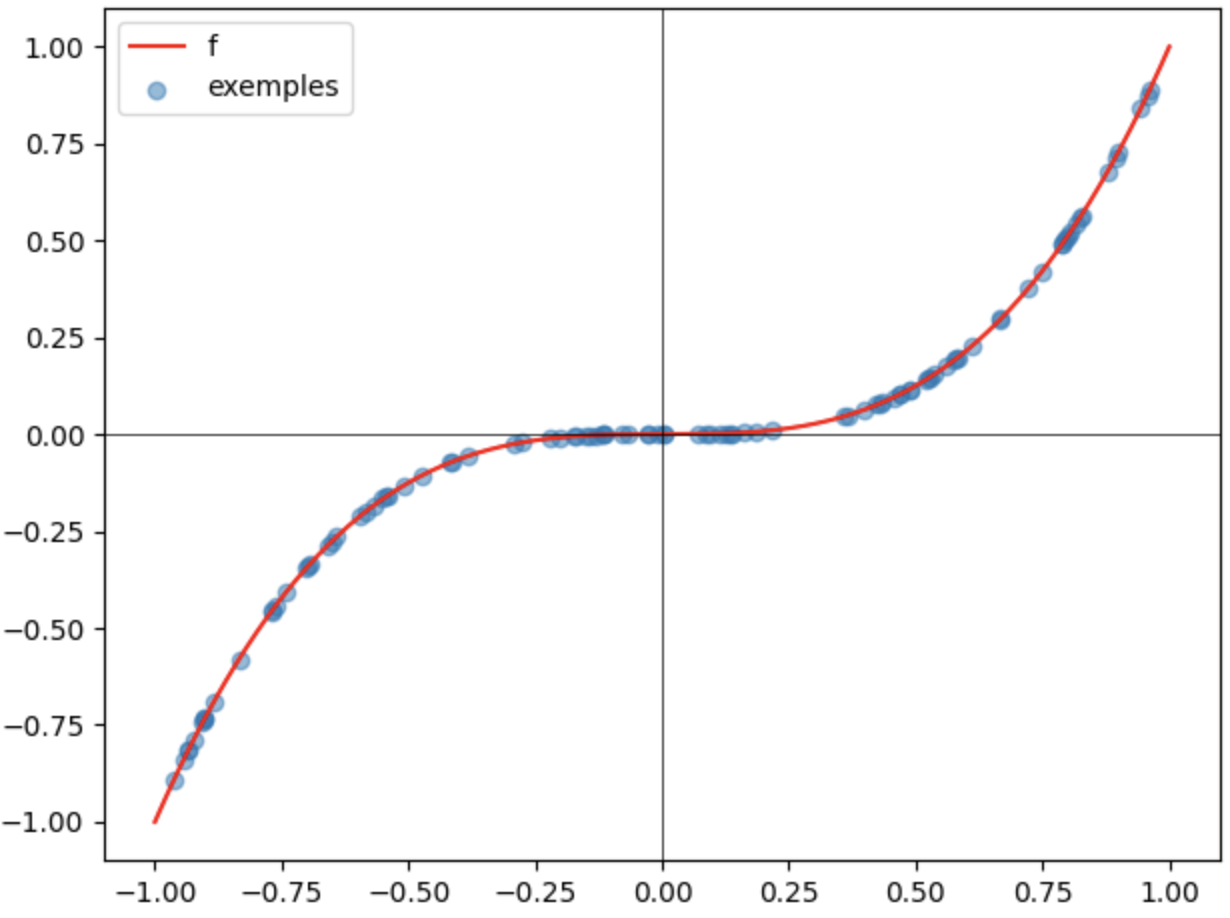
Le points bleus sont les données générées par \(G\), la courbe rouge est la courbe réelle. Sans jamais avoir vu cette courbe, \(G\) apprend à positionner les points qu’il génère près de la courbe.

from IPython.display import Video
Video("videos/GAN1D.mp4",embed =True,width=800)

Apprentissage d’une fonction de \(\mathbb{R}^2\rightarrow \mathbb{R}\)

L’illustration est la même que précédemment, mais pour l’apprentissage d’une surface de \(\mathbb{R}^3\)

from IPython.display import Video
Video("videos/GAN2D.mp4",embed =True,width=800)

Génération de chiffres manuscrits

Le générateur \(G\) apprend à générer le chiffre 9 lorsque \(D\) est entraîné à l’aide des données de MNIST.

from IPython.display import Video
Video("videos/GANMNIST9.mp4",embed =True,width=500)

Implémentation

On propose ici d’implémenter un code permettant de générer des exemples suivant une fonction inconnue \(f: \mathbb{R}\rightarrow \mathbb{R}\) (voir exemple précédent).

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils import data
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

On définit la fonction à reproduire, et on génère des exemples (données réelles).

def f(x):
  return x*x*x

def real_data(n=100,l=-1,h=1):
    X1 = (l+(h-l)*np.random.random(size=n)).reshape(n,1)
    X2 = f(X1).reshape(n,1)
    X = np.hstack((X1, X2))
    
    y = np.ones((n, 1))
    return X, y

x = np.linspace(-1,1,500)
y = f(x)  
plt.plot(x,y,color='red',label='f')
(exemples,_)= real_data()
plt.scatter(exemples[:, 0], exemples[:, 1],alpha=0.5,label='exemples')
plt.axhline(color='black', lw=0.5)
plt.axvline(color='black', lw=0.5)
plt.legend()
plt.tight_layout()

On définit ensuite certains paramètres pour le GAN et l’apprentissage.

data_dim = exemples.shape[-1]
hidden_dim = 5
nbepochs = 8000
batch_size = 100

dataset = data.TensorDataset(torch.Tensor(exemples))
dataloader = data.DataLoader(dataset, batch_size=batch_size)

Le générateur \(G\) et le discriminateur \(D\) sont de simples perceptrons à une couche cachée.

G = nn.Sequential(
    nn.Linear(hidden_dim, 32),
    nn.ReLU(),
    nn.Linear(32, data_dim)
)
G_optimizer = torch.optim.Adam(G.parameters())


D = nn.Sequential(
    nn.Linear(data_dim, 32),
    nn.ReLU(),
    nn.Linear(32, 1),
    nn.Sigmoid()
)
D_optimizer = torch.optim.Adam(D.parameters())

On entraîne enfin le GAN.

for epoch in range(nbepochs):
    for real_data, in dataloader:
        bs = len(real_data)

        # Échantillonne des codes au hasard dans l'espace latent
        z = torch.randn((len(real_data), hidden_dim))
        # Génère les fakes
        fake = G(z)
        # Prédiction de D sur ces données
        predictions = D(fake)

        # Classe "faux" = 0
        fake_labels =  torch.zeros(len(f))
        # Classe "vrai" = 1
        true_labels = torch.ones(len(real_data))

        # Entraîne le générateur
        G_optimizer.zero_grad()
        G_loss = torch.log(1 - predictions).mean()
        G_loss.backward()
        G_optimizer.step()

        # Entraîne le discriminateur
        D_optimizer.zero_grad()
        predictions = D(fake.detach())[:,0]
        true_predictions = D(real_data)[:,0]
        D_loss = 0.5 * (F.binary_cross_entropy(predictions, fake_labels) + F.binary_cross_entropy(true_predictions, true_labels))

        D_loss.backward()
        D_optimizer.step()

Le résultat de l’apprentissage est alors visualisé en fonction des epochs.

[1] (1,2)

Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial nets. In Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger, editors, Advances in Neural Information Processing Systems 27, pages 2672–2680. Curran Associates, Inc., 2014. URL: http://papers.nips.cc/paper/5423-generative-adversarial-nets.pdf.

[2]

Luke Metz, Ben Poole, David Pfau, and Jascha Narain Sohl-Dickstein. Unrolled generative adversarial networks. ArXiv, 2016. URL: https://api.semanticscholar.org/CorpusID:6610705.