Modèles basés énergie#
Pourquoi « énergie » ?#
Alors que la plupart des modèles précédents ont pour objectif initial la classification ou la régression, les modèles basés énergie sont plutôt orientés sur l’estimation de densité. Etant donné un ensemble \(\mathcal E_a\) de données \(\boldsymbol x_i,i\in[\![1,n]\!]\in\mathcal X\), ces modèles recherchent à partir de \(\mathcal E_a\) une distribution de probabilité \(p(\boldsymbol x)\) sur \(\mathcal X\) telle que la vraisemblance d’un \(\boldsymbol x\) est élevée si \(\boldsymbol x\) « ressemble » à une donnée de \(\mathcal E_a\).
L’idée des modèles basés énergie est de transformer toute fonction qui prédit des valeurs positives en une distribution de probabilité en la divisant par son volume. En l’occurrence, les fonctions ciblées seront approchées par des réseaux de neurones.
Soit \(E_{\boldsymbol\theta}\) un réseau de neurones, paramétré par \(\boldsymbol\theta\). Etant donné \(\boldsymbol x\in\mathcal X\), \(E_{\boldsymbol\theta}(\boldsymbol x)\in\mathbb{R}\). On pose alors :
Le vocabulaire « méthodes basées énergie » provient du fait que le réseau calcule une énergie \(f\), et que les points \(\boldsymbol x\) à forte vraisemblance seront d’énergie faible (signe - dans l’exponentielle). L’objectif est alors d’entraîner le réseau de neurones de sorte que \(q_{\boldsymbol\theta}(\boldsymbol x)\) soit la plus proche possible de la distribution inconnue \(p(\boldsymbol x)\) des données dans \(\mathcal X\).
Cette formulation, si facile qu’elle soit à mettre en oeuvre a priori, pose la question du calcul de \(Z_{\boldsymbol\theta}\) (constante de normalisation, assurant que \(q_{\boldsymbol\theta}\) est bien une probabilité). En effet, si \(\mathcal X\) est de grande dimension (ce qui est très souvent le cas, par exemple si on s’intéresse à des images \(\boldsymbol x\) de taille 128\(\times\)128\(\times\)3, alors \(|\mathcal X| = 3^{16384}\)…), alors le calcul est infaisable. En pratique, on ne calcule pas la vraie vraisemblance, mais on utilise des méthodes d’entraînement qui permettent de s’en approcher.
Divergence contrastive#
Dans les modèles génératifs usuels, on maximise la vraisemblance des exemples de l’ensemble d’entraînement \(\mathcal E_a = \{\boldsymbol x_{train}\}\). Puisque la vraisemblance exacte d’un point ne peut pas être déterminée en raison de la constante de normalisation inconnue, il faut ici procéder différemment. On ne peut pas juste maximiser \(e^{-E_{\boldsymbol\theta}(\boldsymbol x_{train})}\), n’ayant aucne garantie que \(Z_{\boldsymbol\theta}\) reste constante. On réécrit alors la maximisation de la vraisemblance en maximisant la probabilité de \(\boldsymbol x_{train}\) en le comparant avec un point de données du modèle échantillonné de manière aléatoire :
On cherche donc à minimiser l’énergie pour les points de données de l’ensemble de données, tout en maximisant l’énergie pour les points de données échantillonnés aléatoirement à partir du modèle. Dans la figure Fig. 56, on cherche à augmenter la probabilité des points de \(\mathcal E_a\), tout en baissant la probabilité de points générés aléatoirement par le modèle. Ces deux objectifs sont atteints si et seulement si \(q_{\boldsymbol\theta}(\boldsymbol x)=p(\boldsymbol x)\). Cet objectif est intuitif et est relié à la distribution \(q_{\boldsymbol\theta}(\boldsymbol x)\) en approximant \(Z_{\boldsymbol\theta}\) par un échantillon de Monte-Carlo.
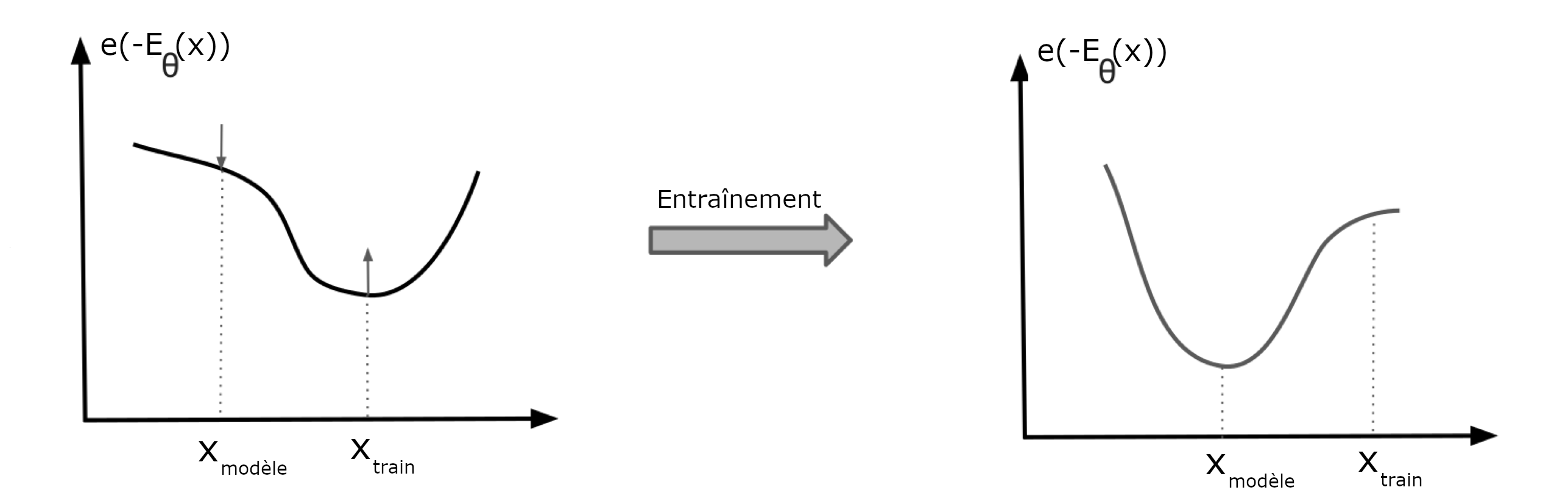
Fig. 80 Optimisation de l’énergie#
Echantillonnage#
Il faut donc pouvoir échantillonner aléatoirement un point à partir du modèle. Pour cela on utilise un algorithme (méthode de Monte Carlo par chaîne de Markov en utilisant la dynamique de Langevin), qui part d’un point aléatoire et se déplace lentement vers la direction de la probabilité la plus élevée en utilisant les gradients de \(E_{\boldsymbol \theta}\) et en ajoutant à chaque déplacement un bruit à l’échantillon courant.
Algorithm 9 (Echantillonnage à partir du modèle)
\(\boldsymbol y_0\sim \mathcal U(.)\) loi uniforme
Pour \(i=1\) à \(N\)
\(\boldsymbol y_i = \boldsymbol y_{i-1}-\eta\nabla_{\boldsymbol x}E_{\boldsymbol\theta}(\boldsymbol y_{i-1}) +\varepsilon\), \(\varepsilon\sim \mathcal N(0,\sigma)\)
\(\boldsymbol x_{modele} = \boldsymbol y_N\)
Implémentation#
Les modèles basés énergie ne sont pas simples à entraîner et peuvent diverger si les hyperparamètres sont mal réglés. Des auteurs (notamment ici) ont proposé des méthodes permettant de pallier ces problèmes, que nous utiliserons dans la suite.
import numpy as np
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.pyplot as plt
from torch.utils.data import Dataset, DataLoader
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import transforms
from sklearn.datasets import load_digits
Le modèle pouvant être long à entraîner, on l’illustre ici sur un petit jeu de données (les digits de scikit-learn).
class Digits(Dataset):
def __init__(self, mode='train', transforms=None):
digits = load_digits()
p_train = 0.7 # Pourcentage d'images d'entraînement
p_val = 0.15 # Pourcentage d'images de validation
nb_images_train = int((p_train)*digits.data.shape[0])
nb_images_val = int((p_train+p_val)*digits.data.shape[0])
if mode == 'train':
self.data = digits.data[:nb_images_train].astype(np.float32)
self.targets = digits.target[:nb_images_train]
elif mode == 'val':
self.data = digits.data[nb_images_train:nb_images_val].astype(np.float32)
self.targets = digits.target[nb_images_train:nb_images_val]
else:
self.data = digits.data[nb_images_val:].astype(np.float32)
self.targets = digits.target[nb_images_val:]
self.transforms = transforms
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
sample_x = self.data[idx]
sample_y = self.targets[idx]
if self.transforms:
sample_x = self.transforms(sample_x)
return (sample_x, sample_y)
transforms_train = transforms.Compose([transforms.Lambda(lambda x: torch.from_numpy(x)),transforms.Lambda(lambda x: x + 0.03 * torch.randn_like(x))])
transforms_val_test = transforms.Compose( [transforms.Lambda(lambda x: torch.from_numpy(x))])
train_data = Digits(mode='train', transforms=transforms_train)
val_data = Digits(mode='val', transforms=transforms_val_test)
test_data = Digits(mode='test', transforms=transforms_val_test)
batch_size = 64
train_loader = DataLoader(train_data, batch_size=batch_size, shuffle=True)
val_loader = DataLoader(val_data, batch_size=batch_size, shuffle=False)
test_loader = DataLoader(test_data, batch_size=batch_size, shuffle=False)
On définit les paramètres et hyperparamètres du problème
D = 64 # Taille de l'entrée du réseau
K = 10 # Nombre de classes (sortie)
M = 512 # Nombre de neurones des couches cachées
sigma = 0.01 # Variance du bruit dans la dynamique de Langevin
eta = 1. # learning rate pour la dynamique de Langevin
N = 20 # Nombre de p as de la dynamique de L ngevin
lr = 1e-3 # Learning rate de l'optimiseur
num_epochs = 20 # Nombre d'epochs
On définit alors le modèle basé énergie
class EnergyBasedModel(nn.Module):
def __init__(self, Etheta, eta, sigma, N, D):
super(EnergyBasedModel, self).__init__()
# Réseau E_theta
self.Etheta = Etheta
# Fonction de perte
self.nlv = nn.nlvLoss(reduction='none')
# Nombre d'entrées du réseau
self.D = D
self.sigma = sigma
self.eta = torch.FloatTensor([eta])
self.N = N
# Classification par le réseau d'un exemple
def classify(self, x):
pred = self.Etheta(x)
y_pred = torch.softmax(pred, 1)
return torch.argmax(y_pred, dim=1)
# Calcule des logits
def classification_loss(self, pred, y):
y_pred = torch.softmax(pred, 1)
return self.nlv(torch.log(y_pred), y)
# Perte associée à x_modele
def gen_loss(self, x, pred):
# Echantillon par dynamique de Langevin
x_sample = self.sample(x=None, batch_size=x.shape[0])
# Calcul de la sortie
f_x_sample_y = self.Etheta(x_sample)
# Réécriture de la maximisation de la vraisemblance
return torch.logsumexp(f_x_sample_y, 1) -torch.logsumexp(pred, 1)
def forward(self, x, y, reduction='avg'):
# Passse avant dans le réseau sur présentation de x
pred = self.Etheta(x)
# Perte en classification par rapport à la vérité
L_gt = self.classification_loss(pred, y)
# Perte en classification par rapport au modèle
L_gen = self.gen_loss(x, pred)
#Fonction objectif
if reduction == 'sum':
loss = (L_gt + L_gen).sum()
else:
loss = (L_gt + L_gen).mean()
return loss
# Calcul du gradient de l'énergie
def energy_gradient(self, x):
self.Etheta.eval()
y_i = torch.FloatTensor(x.data)
y_i.requires_grad = True
y_i_grad = torch.autograd.grad(torch.logsumexp(self.Etheta(y_i), 1).sum(), [y_i], retain_graph=True)[0]
self.Etheta.train()
return y_i_grad
# Pas d'une dynamique de Langevin
def langevin_step(self, y_i1, eta):
# gradient à y(i-1)
grad_energy = self.energy_gradient(y_i1)
# bruit N(0,sigma)
epsilon = torch.randn_like(grad_energy) * self.sigma
# y(i)
y_i = y_i1 + eta * grad_energy + epsilon
return y_i
# Echantillonnage à partir du modèle
def sample(self, batch_size=64, x=None):
# Initialisation, loi uniforme
x_modele = 2. * torch.rand([batch_size, self.D]) - 1.
# Dynamique de Langevin sur N pas
for i in range(self.N):
x_modele = self.langevin_step(x_modele, eta=self.eta)
return x_modele
Etheta = nn.Sequential(nn.Linear(D, M), nn.ELU(),
nn.Linear(M, M), nn.ELU(),
nn.Linear(M, M), nn.ELU(),
nn.Linear(M, K))
model = EnergyBasedModel(Etheta, eta=eta, sigma=sigma, N=N, D=D)
On se donne une fonction d’évaluation du modèle
# Evaluation du modèle
def evaluation(test_loader, name=None, model_best=None, epoch=None):
if model_best is None:
model_best = torch.load(name + '.model')
model_best.eval()
loss = 0.
loss_error = 0.
loss_gen = 0.
n_examples = 0.
for ind, (test_batch, test_targets) in enumerate(test_loader):
# Log vraisemblance négative
loss_test = model_best.forward(test_batch, test_targets, reduction='sum')
loss = loss + loss_test.item()
# Erreur en classification
y_pred = model_best.classify(test_batch)
e = 1.*(y_pred == test_targets)
loss_error = loss_error + (1. - e).sum().item()
# Erreur du modèle
pred_test = model_best.Etheta(test_batch)
loss_gen = loss_gen + model_best.gen_loss(test_batch, pred_test).sum()
n_examples = n_examples + test_batch.shape[0]
loss = loss / n_examples
loss_error = loss_error / n_examples
loss_gen = loss_gen.detach().numpy() / n_examples
return loss, loss_error, loss_gen
et une fonction d’entraînement
# Entrainement du modèle
def training(name, num_epochs, model, optimizer, train_loader, val_loader):
nlv_val = []
gen_val = []
error_val = []
best_nlv = 1000.
for e in range(num_epochs):
model.train()
for ind, (batch, targets) in enumerate(train_loader):
loss = model.forward(batch, targets)
optimizer.zero_grad()
loss.backward(retain_graph=True)
optimizer.step()
# Validation
loss_e, error_e, gen_e = evaluation(val_loader, model_best=model, epoch=e)
print(f'Train Epoch: {e}, log vraisemblance négative={loss_e}, erreur classif={error_e}, erreur modèle={gen_e}')
nlv_val.append(loss_e)
error_val.append(error_e)
gen_val.append(gen_e)
if e == 0:
torch.save(model, name + '.model')
best_nlv = loss_e
else:
if loss_e < best_nlv:
torch.save(model, name + '.model')
best_nlv = loss_e
nlv_val = np.asarray(nlv_val)
error_val = np.asarray(error_val)
gen_val = np.asarray(gen_val)
return nlv_val, error_val, gen_val
et on entraîne le modèle
optimizer = torch.optim.Adamax([p for p in model.parameters() if p.requires_grad == True], lr=lr)
nlv_val, error_val, gen_val = training(name=result_dir + name, num_epochs=num_epochs,model=model, optimizer=optimizer,train_loader=train_loader, val_loader=test_loader)
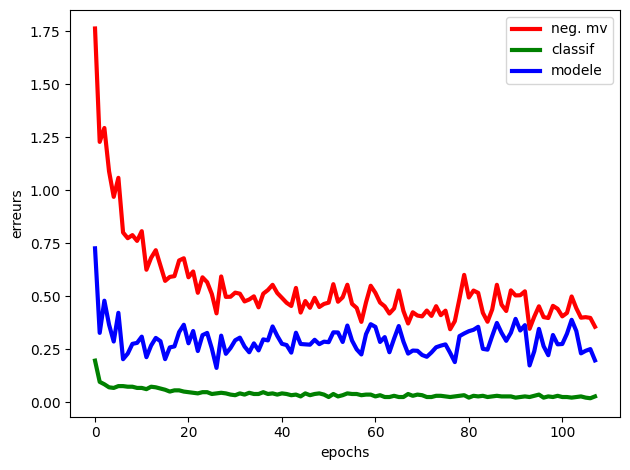
Fig. 81 Evolution des erreurs au cours des epochs#

Fig. 82 Exemple d’images générées (gauche) et de la base d’entraînement (droite)#