Modèle du processus d’apprentissage supervisé#
Un modèle classique de description du processus d’apprentissage supervisé est composé de trois composantes [Vap91]:
Un environnement, qui fournit des vecteurs \(\mathbf x\in X\) avec une probabilité fixe mais inconnue \(P_X\) ;
Un superviseur qui fournit pour chaque vecteur \(\mathbf x\) reçu de l’environnement une réponse désirée \(y\in Y\), selon une probabilité \(P(\mathbf x\mid y)\) fixe mais inconnue. La réponse \(y\) et \(\mathbf x\) sont liés par une relation \(y=f(\mathbf x,\epsilon)\), \(\epsilon\) étant un bruit permettant au superviseur d’être « bruité » ;
Un algorithme d’apprentissage qui implémente une classe de fonctions \(\mathcal{F}\), définies par un paramètre vectoriel \(\boldsymbol{\boldsymbol{\theta}}\), reliant l’espace des vecteurs \(\mathbf x\) à l’espace des réponses \(Y\) : \(\mathcal{F} = \{F(\mathbf x,\boldsymbol{\boldsymbol{\theta}}),\boldsymbol{\theta}\in\boldsymbol{\Theta}\}\)
Le problème de l’apprentissage supervisé consiste alors à choisir dans \(\mathcal{F}\) une fonction qui approche la réponse \(y\) pour tout \(\mathbf x\) d’une manière optimale, au sens statistique du terme. La recherche de cet optimum est basée sur un ensemble de \(n\) exemples i.i.d., dit ensemble d’apprentissage \(Z=\left \{(\mathbf x_i,y_i),i\in[\![1,n]\!],\mathbf x_i\in X,y_i\in Y\right \}\). Chaque exemple \((\mathbf x_i,y_i)\) est tiré par l’algorithme d’apprentissage depuis \(Z\) avec une probabilité jointe fixe mais inconnue \(P_{X,Y}\).
Trouver un « bon » candidat dans \(\mathcal{F}\) qui approche \(f\) repose sur le fait que \(Z\) contient « suffisamment » d’information pour permettre d’une part d’apprendre correctement \(Z\) (facile), mais aussi d’être capable de généraliser de manière cohérente sur \(X\times Y\). La quantification de cette information a été apportée par les travaux de Vapnik et Chervonenkis [VC71].
Soit \(L\left (y,F(\mathbf x,\boldsymbol{\theta})\right )\) une fonction de perte, qui mesure l’écart entre la réponse \(y\) fournie par le superviseur et la réponse calculée par l’algorithme d’apprentissage. L’espérance de \(L\) définit le risque fonctionnel
que l’algorithme d’apprentissage doit donc minimiser sur la classe des fonctions \(\mathcal{F}\).
Cette minimisation est difficile, la probabilité \(P_{X,Y}\) étant inconnue. La seule connaissance sur les couples \((\mathbf x,y)\) est contenue dans \(Z\), et on remplace le problème de minimisation précédent par la minimisation du risque empirique :
qui ne nécessite pas la connaissance de \(P_{X,Y}\).
Remark 1
Une fonction de perte est une fonction \( L : Y\times Y\rightarrow \mathbb R^+\)
Quelques exemples en régression
Pour des problèmes de régression, les fonctions de perte classiques sont :
fonction de perte quadratique, ou perte \(L_2\). : \(L(y,f(\mathbf x)) = (f(\mathbf x)-y)^2\)
fonction de perte \(L_1\) : \(L(f(y,\mathbf x)) = |f(\mathbf x)-y|\) :
fonction de perte de Huber : \(L(y,f(\mathbf x)) = \left \lbrace \begin{array}{ll} \frac{1}{2}(f(\mathbf x)-y)^2 & \textrm{si } |f(\mathbf x)-y|\leq \delta \\ \delta|y-f(\mathbf x)|-\frac{1}{2}\delta^2 & \textrm{sinon } \end{array} \right .\)
fonction de perte de Vapnik: \(L(y,f(\mathbf x)) = \left \lbrace \begin{array}{ll} 0 & \textrm{si } |f(\mathbf x)-y|\leq \epsilon \\ |f(\mathbf x)-y|- \epsilon & \textrm{sinon } \end{array} \right .\) - fonction de perte log cosh: \(L(y,f(\mathbf x)) = log[cosh(f(\mathbf x)-y)]\)
fonction de perte quantile : pour \(\Theta\in [0,1]\) :
\(L(y,f(\mathbf x)) = \displaystyle\sum_{i / y_i< f(\mathbf x_i)} (\Theta -1) |y_i - f(\mathbf x_i)| + \displaystyle\sum_{i / y_i\geq f(\mathbf x_i)} \Theta |y_i - f(\mathbf x_i)| \)
La fonction de perte L1 est plus robuste aux points aberrants que la perte L2, mais n’est pas dérivable partout. La perte de Huber est sensible aux points aberrants, différentiable en 0, et approche la perte L1 ou L2 suivant la valeur de \(\epsilon\).
La perte log cosh approche (à un coefficient 1/2) la perte quadratique pour des petites valeurs de l’argument, et la perte L1 -log(2) pour de grandes valeurs de l’argument.
La fonction de perte quantile permet d’avoir accès à une mesure d’ncertitude sur la prédiction (prédiction d’un intervalle plutôt que d’une valeur).
Quelques exemples en classification
Pour des problèmes de classification binaire en -1/1, les fonctions de perte classiques sont :
fonction de perte charnière : \(L(y,f(\mathbf x)) = (1-yf(\mathbf x))_+ = max\left(0,1-yf(\mathbf x)\right)\)
fonction indicatrice : \(L(y,f(\mathbf x)) =\mathbb{I}_{yf(\mathbf x)\leq 0}\)
fonction de perte logistique : \(L(y,f(\mathbf x)) = ln\left(1+e^{-yf(\mathbf x)}\right)\)
Exemple en estimation de densité
Etant données deux distributions \(p\) et \(q\), une mesure classique de perte entre \(p\) et \(q\) est l’entropie croisée, définie par
où \(H(p)\) est l’entropie de \(p\), et \(D_{KL}\) la divergence de Kullback-Leibler entre \(p\) et \(q\), définie par
Ainsi, si \(p\) est la distribution des \(y\) et \(q\) la distribution des \(f(\mathbf x)\) on peut réécrire
et \(V(f(\mathbf x),y) = -y_i log f(\mathbf x_i)\)
Minimisation du risque empirique#
Soit \(\hat{\boldsymbol{\theta}}\) (respectivement \(F(\mathbf x,\hat{\boldsymbol{\theta}})\)) le vecteur (resp. la fonction) optimal(e) pour le problème de minimisation du risque empirique. Pour une valeur \(\boldsymbol{\theta}^*\in\boldsymbol{\theta}\), le risque \(R(\boldsymbol{\theta}^*)\) est l’espérance d’une certaine variable aléatoire définie par \(M_{\boldsymbol{\theta}^*} = L(y,F(\mathbf x,\boldsymbol{\theta}^*))\). Le risque empirique \(R_{emp}(\boldsymbol{\theta}^*)\), quant à lui, est la moyenne arithmétique de \(M_{\boldsymbol{\theta}^*}\). D’après la loi des grands nombres, si \(n\rightarrow\infty\), la moyenne de \(M_{\boldsymbol{\theta}^*}\) tend vers son espérance, et donc vers \(R(\boldsymbol{\theta}^*)\), ce qui justifie d’utiliser le risque empirique en lieu et place de \(R(\boldsymbol{\theta})\).
Il n’y a cependant aucune raison a priori pour que \(\hat{\boldsymbol{\theta}}\) minimise également \(R(\boldsymbol{\theta})\).
Nous allons montrer que si \(R_{emp}(\boldsymbol{\theta})\) approche uniformément \(R(\boldsymbol{\theta})\) avec une précision \(\epsilon\), alors le minimum du risque empirique s’écarte du minimum de \(R(\boldsymbol{\theta})\) d’au plus \(2\epsilon\).
Supposons
De manière équivalente, puisque pour tout \(\epsilon>0\) on a \(P\left (\displaystyle\sup_{\boldsymbol{\theta}}\mid R(\boldsymbol{\theta})-R_{emp}(\boldsymbol{\theta})\mid>\epsilon\right ) <\alpha\) pour \(\alpha>0\), alors
\(\boldsymbol{\theta}_0\) minimisant \(R(\boldsymbol{\theta})\). Ainsi, si \(P\left (\displaystyle\sup_{\boldsymbol{\theta}}\mid R(\boldsymbol{\theta})-R_{emp}(\boldsymbol{\theta})\mid>\epsilon\right ) <\alpha\) est vraie, alors avec probabilité au moins 1-\(\alpha\) la fonction \(F(\mathbf x,\hat{\boldsymbol{\theta}})\) donnera un risque \(R(\boldsymbol{\hat\theta})\) qui s’écartera du minimum \(R(\boldsymbol{\theta}_0)\) d’au plus \(2\epsilon\).
En effet on a
avec probabilité 1-\(\alpha\) \(\mid R(\boldsymbol{\hat\theta})-R_{emp}(\boldsymbol{\hat\theta})\mid<\epsilon\) et \(\mid R(\boldsymbol{\theta}_0)-R_{emp}(\boldsymbol{\theta}_0)\mid<\epsilon\)
\({\boldsymbol{\hat\theta}}\) et \(\boldsymbol{\theta}_0\) étant les optimum de \(R_{emp}\) et \(R\), \(R_{emp}({\boldsymbol{\hat\theta}})<R_{emp}(\boldsymbol{\theta}_0)\)
Ces trois équations permettent alors d’écrire
La minimisation du risque empirique consiste donc à :
Calculer le risque empirique sur \(Z\) et la valeur \(\boldsymbol{\hat\theta}\) de son paramètre réalisant le minimum de ce risque
Affirmer que \(R(\boldsymbol{\hat\theta})\) converge en probabilité vers le risque minimum sur tout \(X\times Y\), lorsque la taille de l’ensemble d’apprentissage tend vers l’infini, et ce en supposant que \(R_{emp}(\boldsymbol{\theta}\)) converge uniformément vers \(R(\boldsymbol{\theta})\)
Minimisation du risque structurel#
L’erreur d’entraînement \(E_t(\boldsymbol{\theta})\) d’un algorithme d’apprentissage est reliée à la fréquence des erreurs obtenues par cet algorithme sur \(Z\). On demande à un tel algorithme non seulement d’avoir une faible erreur d’entraînement, mais aussi d’être capable de donner des valeurs justes sur des données non vues lors de la phase d’entraînement. On parle de bonne capacité de généralisation.
L’erreur en généralisation \(E_g(\boldsymbol{\theta})\) mesure les erreurs effectuées par l’algorithme sur des exemples qu’il n’a jamais vu, appelés exemples test. On suppose que des exemples sont issus de la même population que les données d’entraînement.
Soit \(h\) la dimension de Vapnik-Chervonenkis d’une famille de classifieurs \(\mathcal{F}\). On peut montrer [Vap91] qu’avec probabilité \(1-\alpha\), pour un nombre d’exemples \(n>h\) que pour toutes les fonctions de \(\mathcal{F}\),
avec
et où
est l’intervalle de confiance. Pour \(n\) fixé, \(E_t(\boldsymbol{\theta})\) décroît lorsque \(h\) augmente, alors que l’intervalle de confiance croît. Ainsi, le risque garanti et l’erreur en généralisation passent par un minimum. Avant cet optimum, le problème d’apprentissage est surdéterminé (\(h\) est trop petit par rapport au niveau d’information contenu dans \(Z\)). Au-delà, il est sous-déterminé (l’algorithme est trop « complexe ») (Fig. 6).
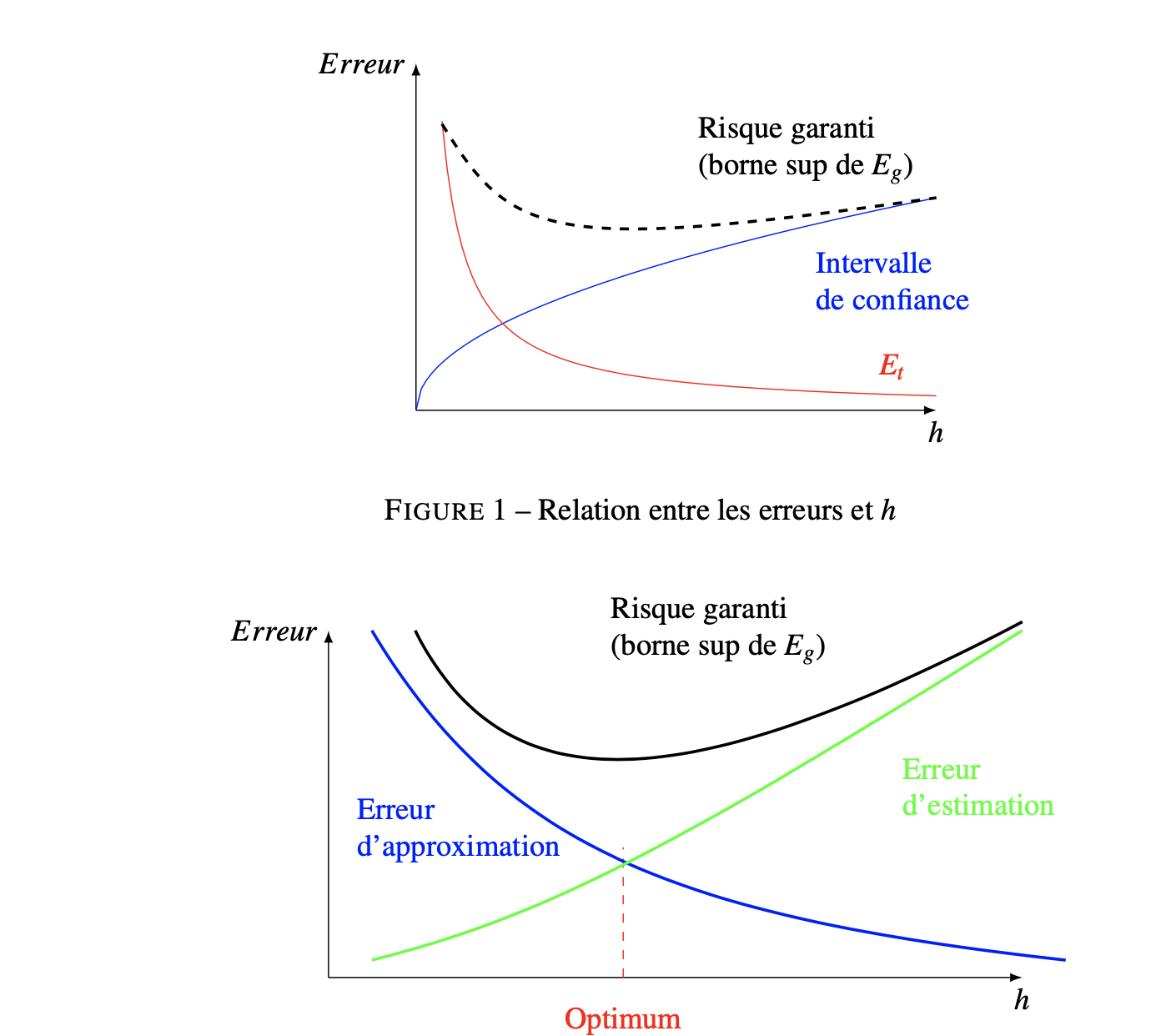
Fig. 6 Relation entre les erreurs et \(h\). L’erreur d’estimation donne une mesure de la performance perdue par la fonction d’approximation en utilisant un ensemble d’apprentissage de taille \(n\). L’erreur d’approximation donne une mesure de performance en fonction de la complexité du modèle#
Un des objectifs dans la résolution d’un problème d’apprentissage supervisé est donc d’atteindre la meilleure capacité de généralisation (minimiser \(E_g(\boldsymbol{\theta})\)). La minimisation du risque structurel propose une méthode inductive permettant d’atteindre cet objectif, en faisant de \(h\) une variable de contrôle.
Soit pour \(k\in[\![1,n]\!]\) \(\mathcal{F}_k=\{F(\mathbf x,\boldsymbol{\theta}),\boldsymbol{\theta}\in\boldsymbol{\theta}_k\}\) un ensemble emboité de classes de fonctions tel que \(\mathcal{F}_1\subset\mathcal{F}_2\ldots \mathcal{F}_n\). Les dimensions de Vapnik-Chervonenkis correspondantes vérifient \(h_1\leq h_2\ldots \leq h_n\). La minimisation du risque structurel consiste à :
Minimiser \(E_t(\boldsymbol{\theta})\) pour chaque fonction
Idenfifier la classe \(\mathcal{F}^*\) dont le risque garanti est le plus faible. Une des fonctions dans \(\mathcal{F}^*\) fournit le meilleur compromis entre \(E_t(\boldsymbol{\theta})\) (qualité d’approximation de \(Z\)) et intervalle de confiance (complexité de la fonction d’approximation).
En pratique, la variation de \(h\), et donc la création des ensembles emboîtés, peut être réalisée dans des réseaux de neurones à nombre de neurones cachés croissant.
Thomas M. Cover. Geometrical and statistical properties of systems of linear inequalities with applications in pattern recognition. Electronic Computers, IEEE Transactions on, EC-14(3):326–334, 1965. URL: http://hebb.mit.edu/courses/9.641/2002/readings/Cover65.pdf.
V. N. Vapnik and A. Ya. Chervonenkis. On the uniform convergence of relative frequencies of events to their probabilities. Theory of Probability and its Applications, 16(2):264–280, 1971.