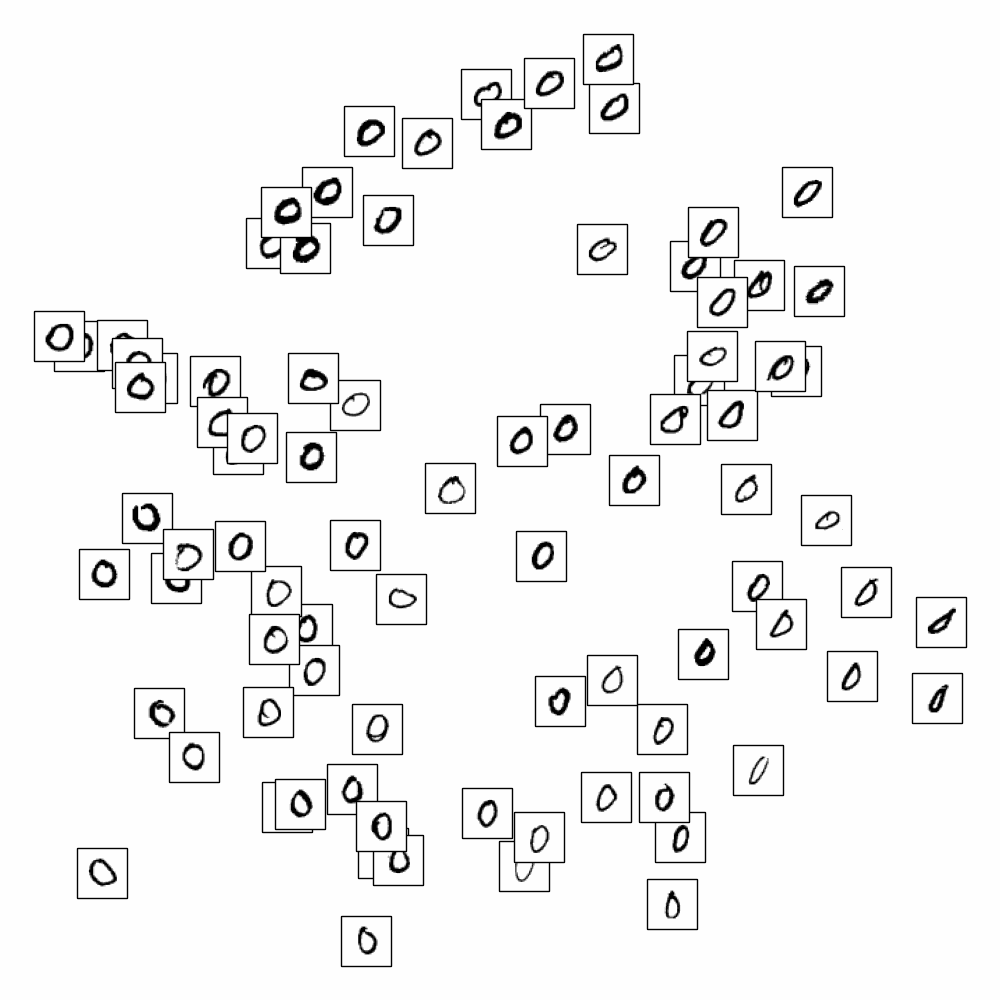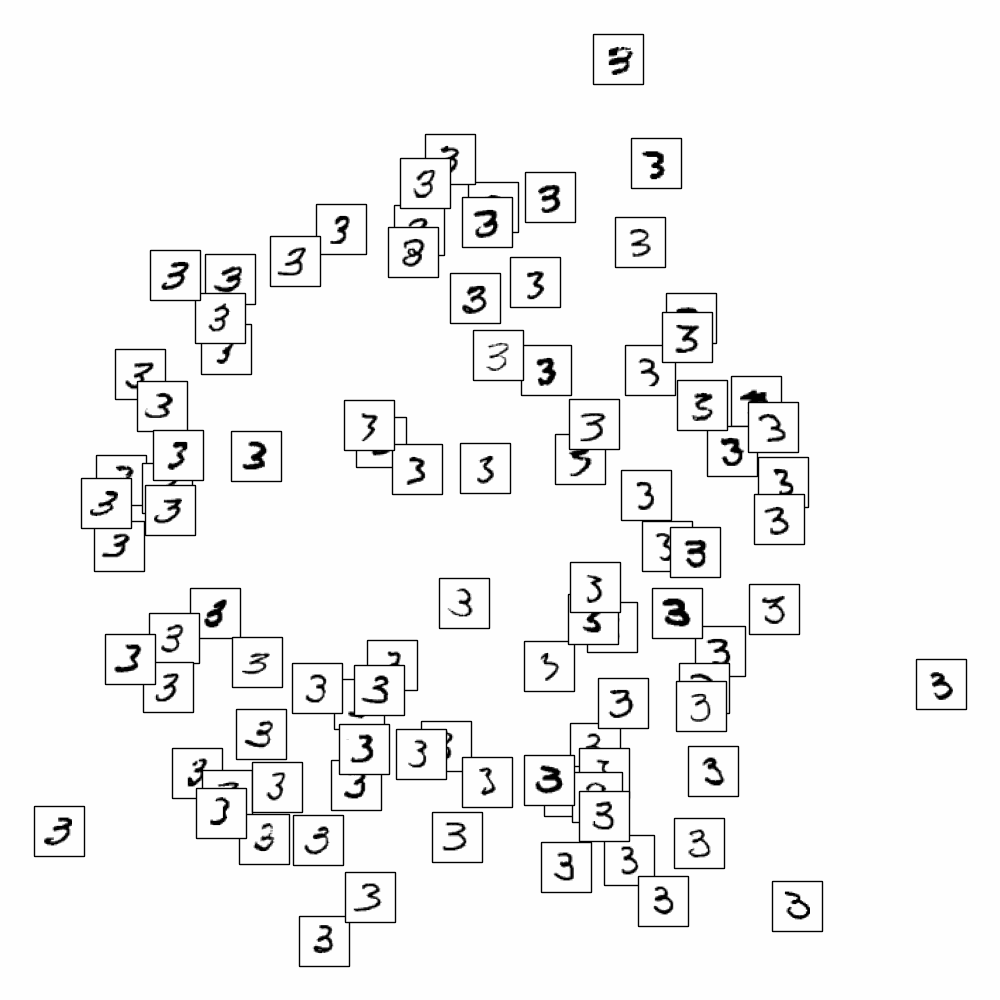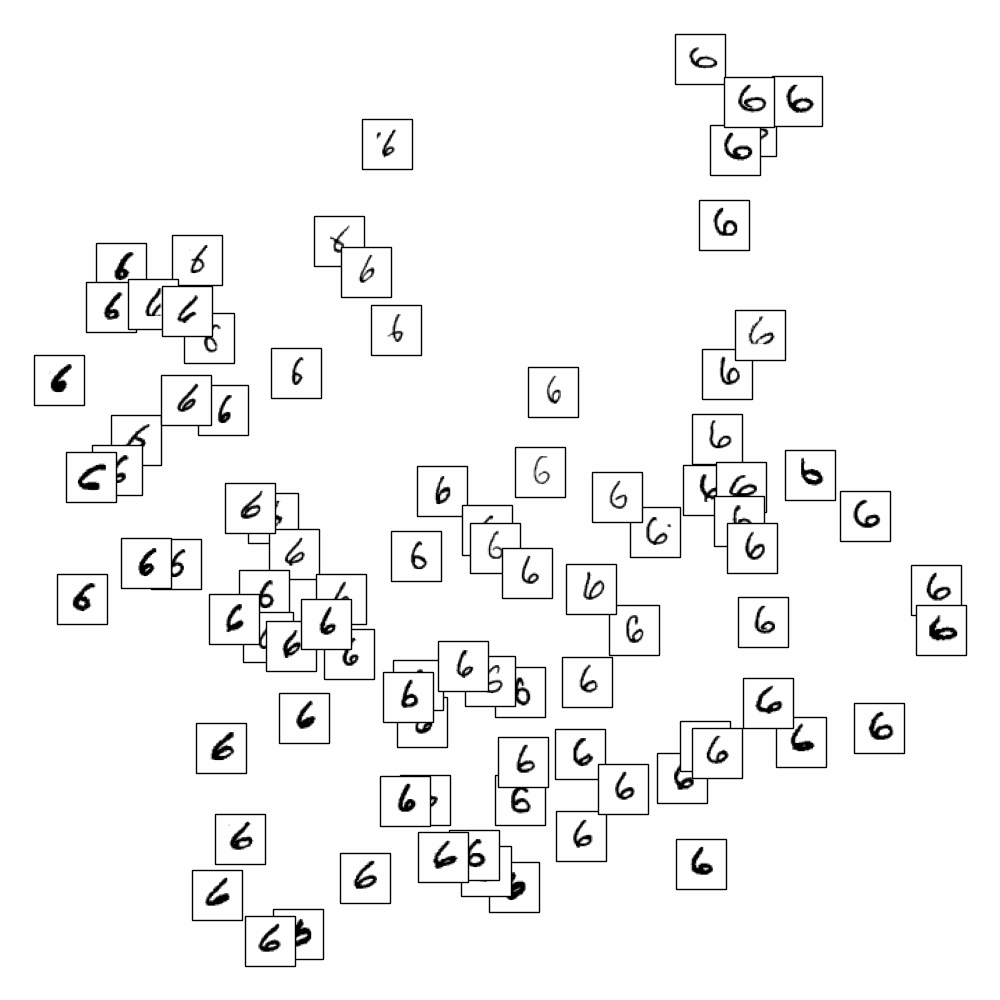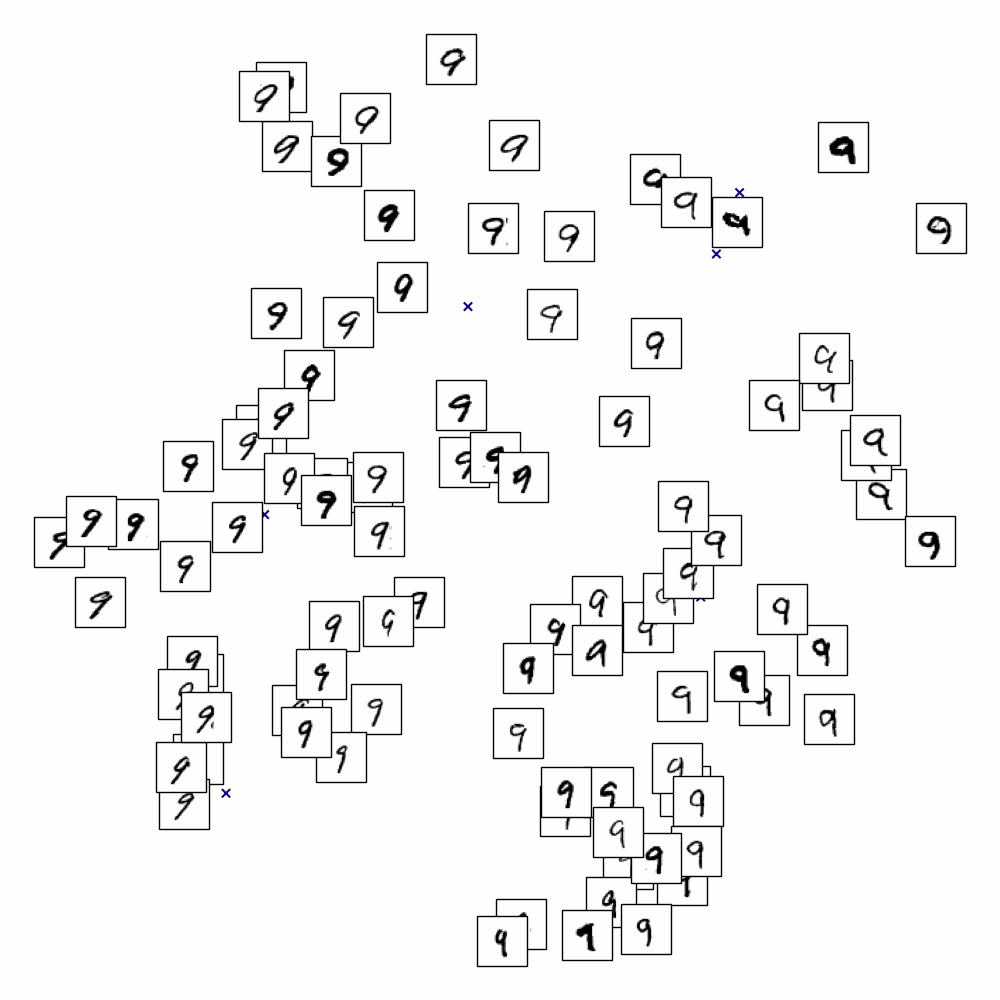Local Linear Embedding

L’algorithme de plongement localement linéaire (Local Linear Embedding, LLE) est similaire dans l’esprit à ISOMAP, mais agit d’un point de vue local puisqu’il tente de préserver les informations locales sur la variété riemannienne plutôt que d’estimer les distances géodésiques.

Algorithme

1. Recherche des plus proches voisins : pour \(K_i<<d\), on note \(N_i^{K_i}\) le voisinage de \(\mathbf x_i\) composé de ses \(K_i\) plus proches voisins, calculés en utilisant la distance euclidienne. \(K_i\) est indicé par \(i\) car il peut être différent pour chaque point de donnée.

2. Reconstruction par moindres carrés contraints : en faisant l’approximation d’ordre 1 que, localement, une variété est linéaire, on reconstruit \(x_i\) comme combinaison linéaire de ses \(K_i\) plus proches voisins :

\[x_i = \displaystyle\sum_{j\in K_i} w_{ij}\mathbf x_j = \displaystyle\sum_{j=1}^n w_{ij}\mathbf x_j\]

On impose aux \(w_{ij}\) de sommer à 1 pour être invariant en translation, et si la somme est effectuée pour tous les points, alors \(w_{ij}=0\) si \(\mathbf x_j\notin N_i^{K_i}\). On note \(W=\left (w_{ij}\right )\) et on cherche les pondérations \(\hat{w}_{ij}\) résolvant le problème d’optimisation contraint :

\[\begin{split} \displaystyle\min_W&&\displaystyle\sum_{i=1}^n \|\mathbf x_i-\displaystyle\sum_{j=1}^nw_{ij}\mathbf x_j\|^2\\ s.c&& (\forall i\in\{1\cdots n\})\quad\displaystyle\sum_{j=1}^nw_{ij}=1 \\ &&(\forall i\in\{1\cdots n\}) \quad w_{ij}=0 \textrm{ si } \mathbf x_j\notin N_i^{K_i} \end{split}\]

Pour \(i\in[\![1,n]\!]\), on note

\[\left \| \displaystyle\sum_{j=1}^n w_{ij}(\mathbf x_i-\mathbf x_j)\right \|^2=\mathbf w_i^TG_i\mathbf w_i\]

où \(\mathbf w_i=(w_{i1}\cdots w_{in})^T\in\mathbb{R}^n\) et \(G_i\) est la matrice de Gram associée à \(\mathbf x_i\), de coefficients

\[G_{jk}=(\mathbf x_i-\mathbf x_j)^T(\mathbf x_i-\mathbf x_k),j,k\in N_i^{K_i}\]

La relaxation lagrangienne du problème d’optimisation amène à minimiser

\[\mathbf w_i^TG_i\mathbf w_i -\lambda(1_n^T\mathbf w_i-1)\]

où \(\lambda\) est le multiplicateur de Lagrange associé à la contrainte de somme unité, et \(1_n\) est le vecteur de \(\mathbb{R}^n\) composé uniquement de 1. L’annulation de la dérivée partielle par rapport à \(\mathbf w_i\) donne \(\hat{\mathbf w}_i=\frac{\lambda}{2}G_i^{-1}1_n\). En multipliant à gauche par \(1_n^T\), on obtient finalement

\[\hat{\mathbf w}_i=\frac{G_i^{-1}1_n}{1^T_nG_i^{-1}1_n}\]

On forme alors \(\hat{W}\) la matrice dont les colonnes sont les \(\hat{\mathbf w}_i\).

3. Plongement spectral : on recherche enfin la matrice \(Y\) de taille \(t\times n\) donnant les vecteurs \(\mathbf y_i\) en résolvant le problème d’optimisation

\[\begin{split} \displaystyle\min_Y&&\displaystyle\sum_{i=1}^n \|\mathbf y_i-\displaystyle\sum_{j=1}^n\hat{w}_{ij}\mathbf y_j\|^2\\ s.c&&Y1_n= \displaystyle\sum_{i=1}^n \mathbf y_i=0\in\mathbb{R}^t \\ &&\frac{1}{n}YY^T=\frac{1}{n}\displaystyle\sum_{i=1}^n \mathbf y_i\mathbf y_i^T=I\in \mathcal{M}_t(\mathbb{R}) \end{split}\]

Les contraintes déterminent le positionnement (translation, rotation, échelle) des coordonnées \(\mathbf y_i\). \

La fonction objectif peut être réécrite

\[Tr(YMY^T)\]

avec \(M=(I-\hat{W})^T(I-\hat{W})\). Cette fonction a un minimum global unique donné par les vecteurs propres correspondant aux t+1 plus petites valeurs propres de \(M\), associées aux vecteurs propres \(\mathbf{v}_n\cdots \mathbf{v}_{n-t}\). La plus petite d’entre elles est 0, correspondant à \(\mathbf{v}_n=\frac{1}{\sqrt{n}}1_n\). Puisque la somme des coefficients de chacun des autres vecteurs propres, qui sont orthogonaux à \(\mathbf{v}_n\), est zéro, ignorer \(v_n\) et sa valeur propre associée contraindra les coordonnées \(\mathbf y_i\) d’être de somme nulle. La solution optimale est donc

\[Y = \left (\mathbf{v}_{n-1}\cdots \mathbf{v}_{n-t}\right )\in\mathcal{M}_{t,n}(\mathbb{R})\]

On applique LLE sur les données MNIST et on cherche à représenter les images (vecteurs de \(\mathbb{R}^{784}\)) dans \(\mathbb{R}^{2}\)

from IPython.display import Video
Video("videos/lle.mp4",embed =True,width=800)

Contrairement à ISOMAP, LLE gère assez bien les variétés non convexes, puisque l’algorithme préserve les propriétés géométriques locales, plutôt que globales. En, revanche, les variétés à trou sont également difficiles à traiter par cet algorithme.

Exemple d’application

On applique LLE sur les données MNIST et on cherche à représenter les images (vecteurs de \(\mathbb{R}^{784}\)) dans \(\mathbb{R}^{2}\)

En affichant uniquement les chiffres de 0 à 9, on s’aperçoit que LLE sépare également les styles pour un même chiffre.