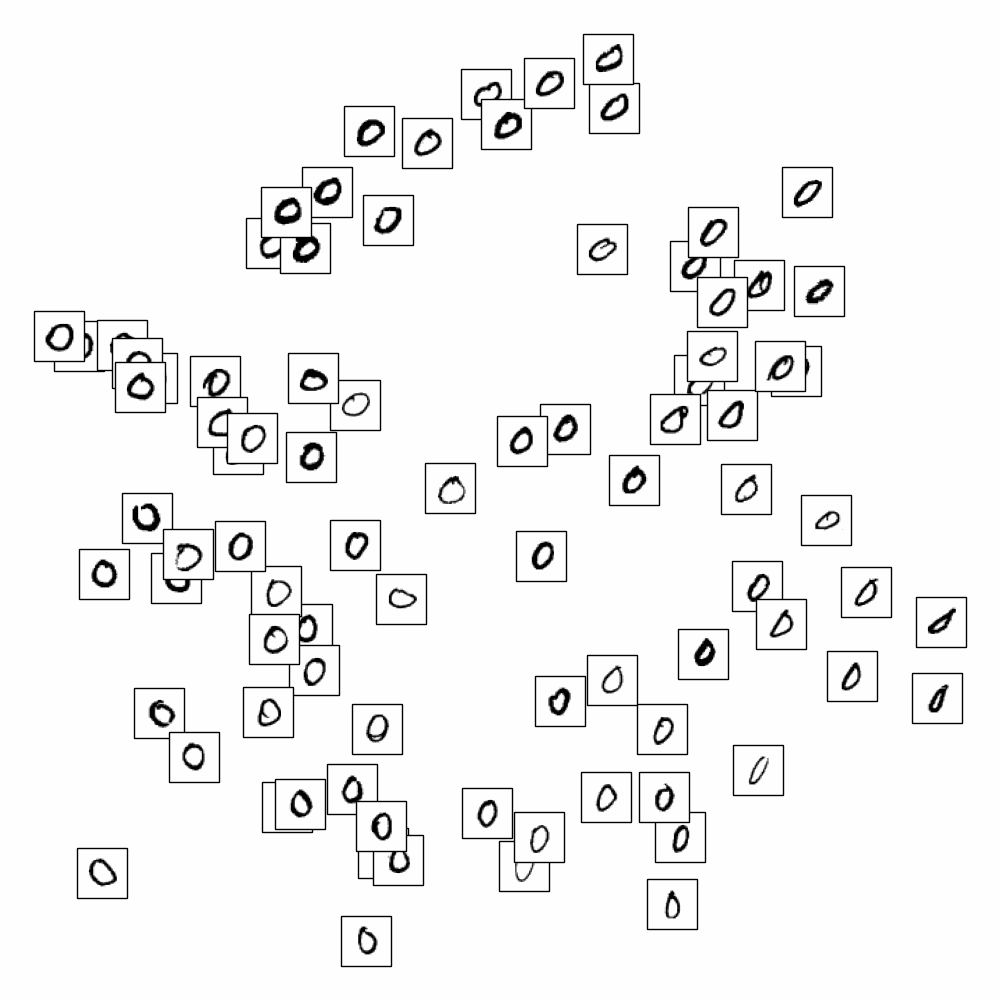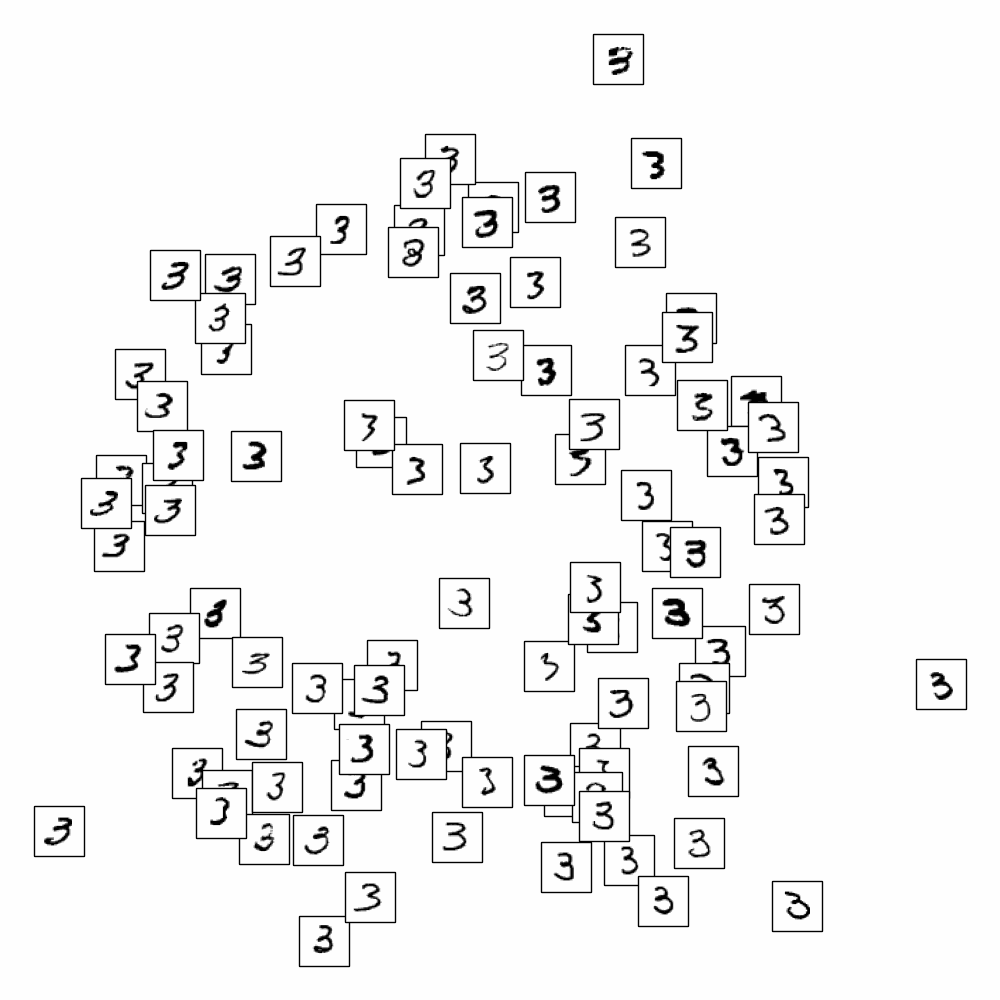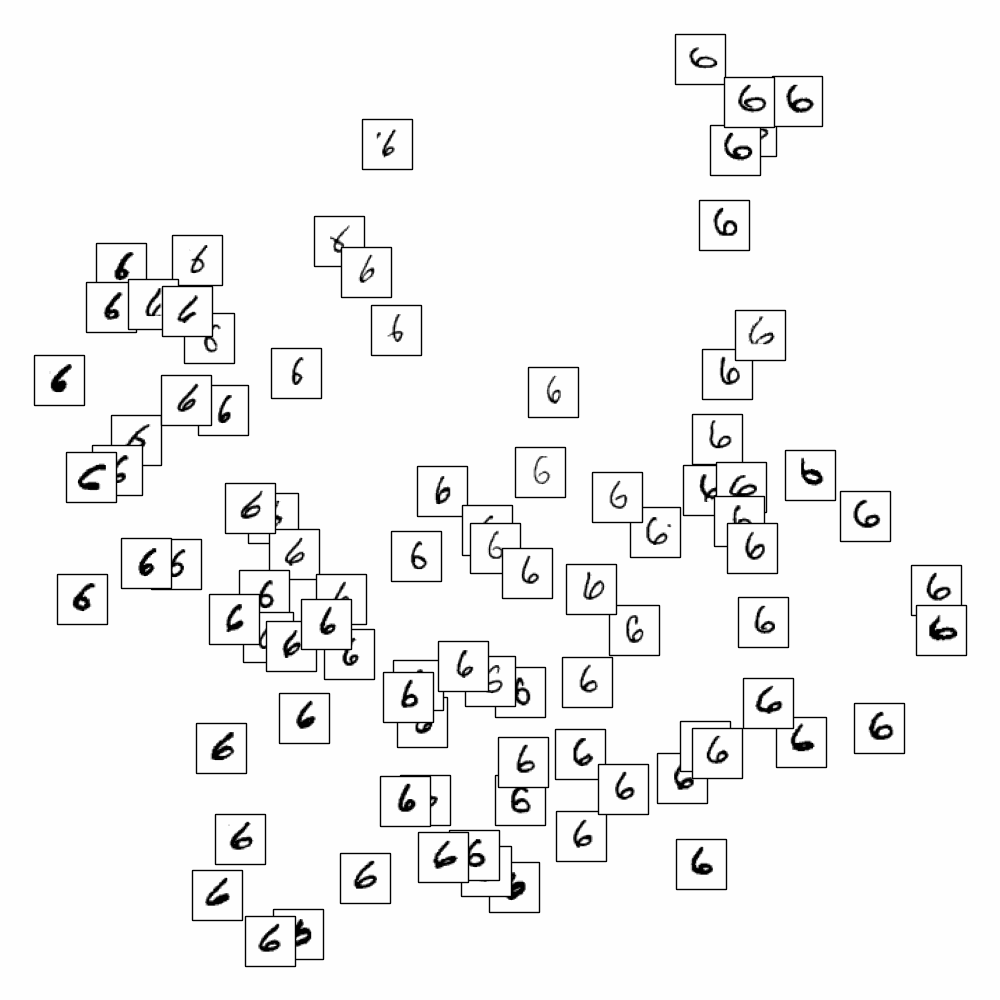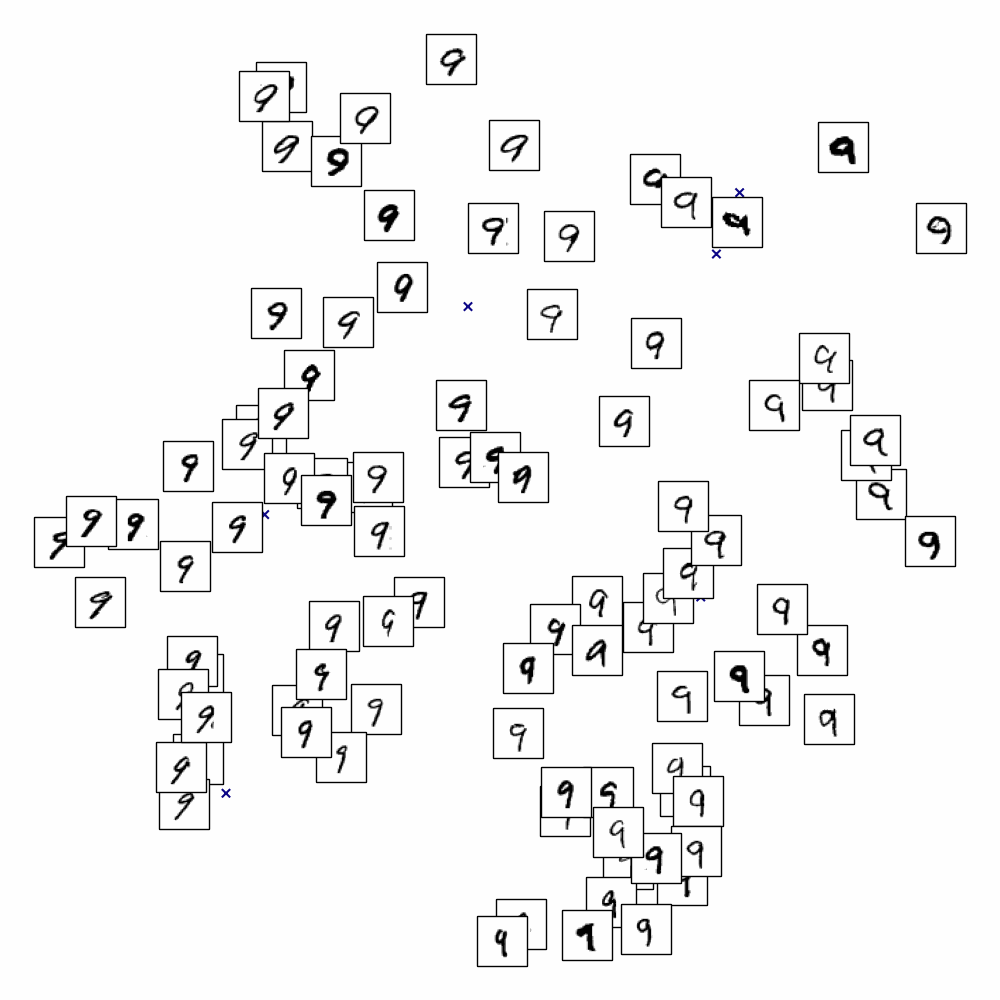ISOMAP#
L’algorithme Isometric Feature Mapping (ISOMAP) suppose que \(\mathcal{M}\) est un convexe de \(\mathbb{R}^t\) et que le plongement \(\psi\) est une isométrie : pour chaque paire de points \(\mathbf y_i,\mathbf y_j\in\mathcal{M}\), la distance géodésique entre \(\mathbf y_i\) et \(\mathbf y_j\) est égale à la distance euclidienne entre leurs coordonnées \(\mathbf x_i, \mathbf x_j\) sur \(\mathcal{X}\) :
L’algorithme ISOMAP utilise ces deux hypothèses pour proposer une généralisation non linéaire de MDS. La méthode tente de préserver les propriétés géométriques globales de la variété \(\mathcal{M}\) sous-jacente en approximant toutes les distances géodésiques entre paires de points \(\mathbf y_i\).
Algorithme#
Plus précisément, ISOMAP fonctionne en trois étapes :
Recherche des plus proches voisins : ISOMAP calcule tout d’abord toutes les paires de distances \(\|\mathbf x_i-\mathbf x_j\|\), pour \(i,j\in[\![1,n]\!]\). Une sélection des points voisins est ensuite effectuée, soit en ne retenant pour chaque point que \(K\) plus proches voisins, soit en retenant tous les points inclus dans une boule de rayon \(\epsilon>0\). \(K\) (ou \(\epsilon\)) est un paramètre de l’algorithme
Calcul du graphe de voisinage : un graphe \(\mathcal{G}(\mathcal{V},\mathcal{E})\) est ensuite construit, où \(\mathcal{V}=(\mathbf x_1\cdots \mathbf x_n)\) et \(\mathcal{E}=(e_{ij})\) est un ensemble d’arcs reliant les points voisins au sens de \(K\) (ou \(\epsilon\)), pondérés par des poids \(w_{ij}=\|\mathbf x_i-\mathbf x_j\|\). Si deux points ne sont pas voisins, aucun arc ne relie ces points et le poids est nul. Les distances géodésiques entre points \(\mathbf y_i\) et \(\mathbf y_j\) de \(\mathcal{M}\) sont alors estimées par le calcul des plus courts chemins \(d^\mathcal{G}_{ij}\) entre les paires de points correspondants \(\mathbf x_i\) et \(\mathbf x_j\) de \(\mathcal{G}\).
Plongement spectral par MDS : l’application de l’algorithme de positionnement multidimensionnel à la matrice symétrique de taille \(n\) composée des plus courts chemins entre les points \(\mathbf x_i\) permet de reconstruire les points dans un espace de dimension \(t\) , de sorte que les distances géodésiques sur \(\mathcal{M}\) soient préservées au mieux :
Si \(S=\left (\left (d^\mathcal{G}_{ij} \right )^2\right )\), on calcule \(A=-\frac{1}{2}HSH\), \(H=I-\frac{1}{n}J\), \(J\) étant une matrice \(n\times n\) de coefficients tous égaux à 1. \(A\) est semi définie positive de rang \(t<n\)
Si \(\hat{S}=\left (\|\mathbf y_i-\mathbf y_j\|^2 \right )\), la minimisation de \(\|A-(-\frac{1}{2}H\hat{S}H)\|\) permet d’obtenir les vecteurs reconstruits \(\hat{\mathbf y_i}\). La solution optimale est obtenue à l’aide des vecteurs propres \(\mathbf{v}_1\cdots \mathbf{v}_t\) correspondant aux \(t\) plus grandes valeurs propres \(\lambda_1>\cdots \lambda_t\) de \(A\).
La \(i^e\) colonne de la matrice \(Y=\left (\sqrt{\lambda_1}\mathbf{v}_1\cdots \sqrt{\lambda_t}\mathbf{v}_t\right)^T\) donne les coordonnées du \(i^e\) point dans \(\mathbb{R}^t\)
from IPython.display import Video
Video("videos/isomap.mp4",embed =True,width=800)
Propriétés#
ISOMAP fonctionne mal sur des variétés à trous, la contrainte de convexité étant violée. De plus, dans le cas de données bruitées (i.e. n’étant pas précisément sur la variété), l’influence de \(K\) (ou \(\epsilon\)) joue beaucoup : si les valeurs des paramètres sont trop grandes (faux arcs dans \(\mathcal{G}\)) ou trop petites (\(\mathcal{G}\) a trop peu d’arcs pour approximer de manière correcte les distances géodésiques), l’algorithme échoue.
Enfin, empiriquement, il a été montré que l’algorithme fonctionnait moins bien lorsque \(n\) est grand, et on lui préférera l’algorithme Landmark ISOMAP dans ce cas.
Exemple d’application#
On applique ISOMAP sur les données MNIST et on cherche à représenter les images (vecteurs de \(\mathbb{R}^{784}\)) dans \(\mathbb{R}^{2}\)
from sklearn.datasets import fetch_openml
import numpy as np
import matplotlib.pyplot as plt
X, y = fetch_openml('mnist_784', version=1, parser='auto', return_X_y=True)
X = X.to_numpy()
y = y.astype(np.int8)
n_samples, n_features = X.shape
n_neighbors = 30
def plot_mnist(X, y, X_embedded, min_dist=10.0):
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(frameon=False)
plt.setp(ax, xticks=(), yticks=())
plt.subplots_adjust(left=0.0, bottom=0.0, right=1.0, top=0.9,
wspace=0.0, hspace=0.0)
plt.scatter(X_embedded[:, 0], X_embedded[:, 1],
c=y,cmap=plt.cm.plasma,marker="x")
if min_dist is not None:
from matplotlib import offsetbox
shown_images = np.array([[10., 10.]])
indices = np.arange(X_embedded.shape[0])
np.random.shuffle(indices)
for i in indices[:5000]:
dist = np.sum((X_embedded[i] - shown_images) ** 2, 1)
if np.min(dist) < min_dist:
continue
shown_images = np.r_[shown_images, [X_embedded[i]]]
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(X[i].reshape(28, 28),
cmap=plt.cm.gray_r), X_embedded[i])
ax.add_artist(imagebox)
plt.tight_layout()
rndperm = np.random.permutation(X.shape[0])
n_iso = 7000
Xr = X[rndperm[:n_iso]]
yr = y[rndperm[:n_iso]]
from sklearn.manifold import Isomap
X_iso = Isomap(n_neighbors=n_neighbors, n_components=2).fit_transform(Xr)
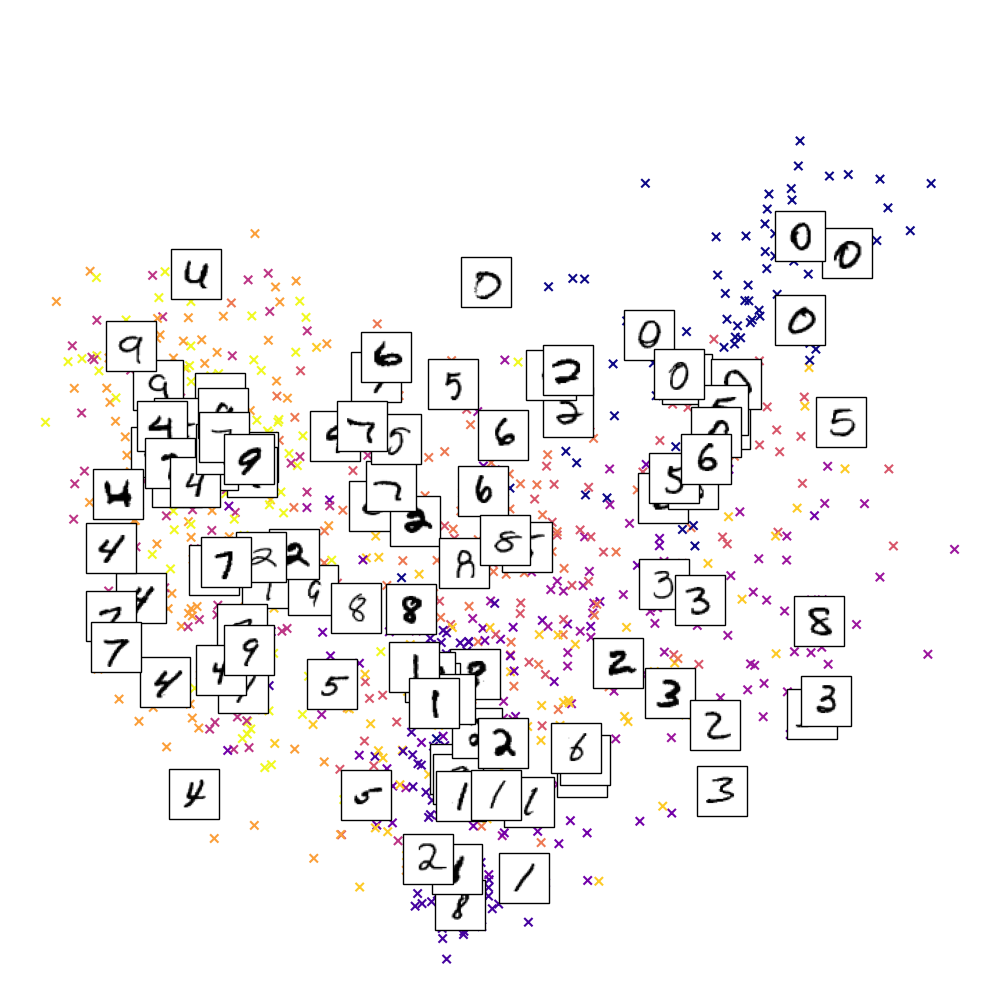
En affichant uniquement les chiffres de 0 à 9, on s’aperçoit qu’ISOMAP sépare également les styles (par exemple les 1 sont penchés de gauche à droite, les 7 avec un barre sont regroupés)