!pip3 install --quiet seaborn numpy matplotlib pandas mca
error: externally-managed-environment
× This environment is externally managed
╰─> To install Python packages system-wide, try brew install
xyz, where xyz is the package you are trying to
install.
If you wish to install a Python library that isn't in Homebrew,
use a virtual environment:
python3 -m venv path/to/venv
source path/to/venv/bin/activate
python3 -m pip install xyz
If you wish to install a Python application that isn't in Homebrew,
it may be easiest to use 'pipx install xyz', which will manage a
virtual environment for you. You can install pipx with
brew install pipx
You may restore the old behavior of pip by passing
the '--break-system-packages' flag to pip, or by adding
'break-system-packages = true' to your pip.conf file. The latter
will permanently disable this error.
If you disable this error, we STRONGLY recommend that you additionally
pass the '--user' flag to pip, or set 'user = true' in your pip.conf
file. Failure to do this can result in a broken Homebrew installation.
Read more about this behavior here: <https://peps.python.org/pep-0668/>
note: If you believe this is a mistake, please contact your Python installation or OS distribution provider. You can override this, at the risk of breaking your Python installation or OS, by passing --break-system-packages.
hint: See PEP 668 for the detailed specification.
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
%matplotlib inline
TP AFC / ACM#
Exercice 1 : Analyse Factorielle des Correspondances#
Le fichier de données est un tableau d’effectifs, croisant l’origine sociale des sondés (CSP, version simplifiée) avec les médias d’informations utilisés
media = pd.read_table("./data/mediaCSP.txt", header=0, index_col=0, delimiter="\t", encoding="utf-8")
print(media)
Radio Tel. Quot.Nat. Quot.Reg. Press.Mag. Press.TV
Prof
Agriculteur 96 118 2 71 50 17
Petit.Patr. 122 136 11 76 49 41
Prof.Cad.Sup 193 184 74 63 103 79
Prof.Int. 360 365 63 145 141 184
Employe 511 593 57 217 172 306
Ouvr.Qualif. 385 457 42 174 104 220
Ouvr.Non-Qual. 156 185 8 69 42 85
Inactif 1474 1931 181 852 642 782
===== Votre travail : =====#
Vous avez à disposition un fichier ca.py, permettant de réaliser les calculs relatifs à une analyse factorielle des correspondances. L’objectif est de répondre aux questions suivantes :
Quelle est la structure des moyens d’information choisis selon la CSP ? (profils lignes).
La structure est-elle différente d’une CSP à l’autre ?
Les médias sont-ils différents en termes de CSP ? (profils colonnes)
Existe-t-il des relations entre CSP et médias (des CSP ont-elles une préférences pour certains médias ? Certains médias attirent-ils des catégories particulières de CSP ?)
Analyse Factorielle des correspondances#
On créé une instance de l’objet CA, que l’on applique sur le tableau des valeurs
from ca import CA
afc = CA(row_labels=media.index,col_labels=media.columns)
afc.fit(media.values)
CA(col_labels=Index(['Radio', 'Tel.', 'Quot.Nat.', 'Quot.Reg.', 'Press.Mag.', 'Press.TV'], dtype='object'),
row_labels=Index(['Agriculteur', 'Petit.Patr.', 'Prof.Cad.Sup', 'Prof.Int.', 'Employe',
'Ouvr.Qualif.', 'Ouvr.Non-Qual.', 'Inactif'],
dtype='object', name='Prof'))In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
CA(col_labels=Index(['Radio', 'Tel.', 'Quot.Nat.', 'Quot.Reg.', 'Press.Mag.', 'Press.TV'], dtype='object'),
row_labels=Index(['Agriculteur', 'Petit.Patr.', 'Prof.Cad.Sup', 'Prof.Int.', 'Employe',
'Ouvr.Qualif.', 'Ouvr.Non-Qual.', 'Inactif'],
dtype='object', name='Prof'))Valeurs propres#
En utilisant l’attribut \(eig\_\) et la fonction plot_eigenvalues (ligne 294 du fichier \(base.py\)),afficher et interpréter les valeurs propres issues de l’analyse factorielle (nombre, contribution des facteurs…)
#TODO
#TODO
Analyse des profils lignes#
On affiche ici, pour chaque modalité ligne, la distribution des individus colonnes
data = np.apply_along_axis(arr=media.values,axis=1,func1d=lambda x:x/np.sum(x))
data_cum = data.cumsum(axis=1)
labels = list(media.index)
colors = plt.get_cmap('RdYlGn')(np.linspace(0.15, 0.85, data.shape[1]))
fig, ax = plt.subplots(figsize=(9.2, 5))
ax.invert_yaxis()
ax.xaxis.set_visible(False)
ax.set_xlim(0, np.sum(data, axis=1).max())
for i, (colname, color) in enumerate(zip(list(afc.col_labels_short_.values), colors)):
widths = data[:,i]
starts = data_cum[:,i] - widths
ax.barh(labels, widths, left=starts, height=0.5,label=colname, color=color)
xcenters = starts + widths / 2
r, g, b, _ = color
text_color = 'white' if r * g * b < 0.5 else 'darkgrey'
for y, (x, c) in enumerate(zip(xcenters, widths)):
ax.text(x, y, str(float(round(c,2))), ha='center', va='center',
color=text_color)
ax.legend(ncol=len(afc.col_labels_short_.values), bbox_to_anchor=(0, 1),
loc='lower left', fontsize='small')
plt.show()
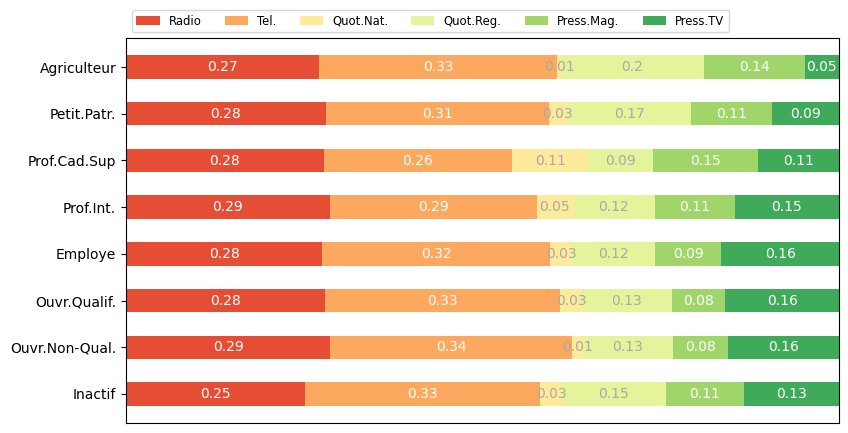
En utilisant l’attribut row_coord_, afficher les coordonnées des modalités lignes par facteur. Calculer la moyenne pondérée et la variance des coordonnées des modalités lignes sur le premier facteur. Qu’obtenez-vous ?
#TODO
#TODO
Moyenne : 1.3877787807814457e-17 égale à 0
Variance : 0.013857286816774693 égale à la valeur propre associée
En utilisant la fonction mapping_row (ligne 389, ficher base.py), représenter les individus lignes dans le premier plan factoriel (qui restitue 94.5% de l’information disponible). Analyser le résultat
#TODO
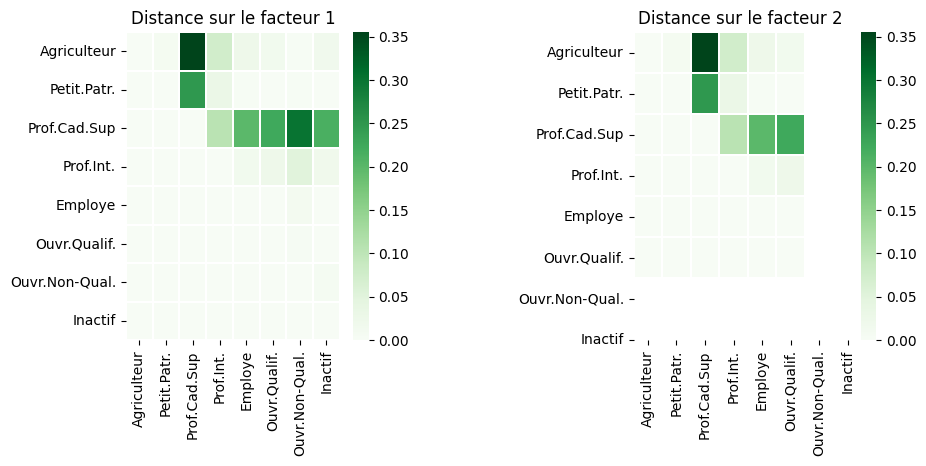
Calcul de la distance du \(\chi^2\)#
La distance du \(\chi^2\) entre les modalités lignes dans l’espace initial devient distance euclidienne dans l’espace factoriel. Comme en ACP, la restitution est parfaite lorsque tous les facteurs sont pris en compte, et approchée si une partie est utilisée. La précision dépend alors d’une part de la qualité de restitution du repère factoriel choisi, d’autre part de la qualité de représentation des modalités impliquées dans le calcul (les \(cos^2\)).
f,ax = plt.subplots(1, 2,figsize=(10,4))
for l in range(0,2):
# Distances entre modalités sur le l-eme facteur
plt.subplot(1,2,l+1)
distPairesLigF1 = np.zeros(shape=(data.shape[l],data.shape[l]))
for i in range(data.shape[l]-1):
for j in range(i+1,data.shape[l]):
distPairesLigF1[i,j] = np.sum((afc.row_coord_[i,0]-afc.row_coord_[j,0])**2)
sns.heatmap(distPairesLigF1,vmin=0,vmax=np.max(distPairesLigF1),linewidth=0.1,cmap= 'Greens',xticklabels=media.index,yticklabels=media.index)
plt.title("Distance sur le facteur "+str(l+1))
f.subplots_adjust(wspace=0.9)
Analyse des profils colonnes#
Faire la même analsye sur les profils colonnes. Interpréter les résultats
#TODO
Analyse de l’association lignes-colonnes#
Au-delà de la comparaison des profils, l’intérêt majeur de l’AFC est d’identifier les associations entre les modalités lignes et colonnes : est ce que les agriculteurs s’informent plus par la radio que les autres ? Est ce que la presse magazine attire plus les cadres ?
Avant de s’intéresser aux relations entre les modalités, il faut déjà vérifier qu’il existe bien une liaison exploitable entre les variables en ligne et colonne du tableau de contingence. La statistique du \(\chi^2\) de l’écart à l’indépendance permet de le faire
Faire un test du \(\chi^2\) (voir le cours statistiques bivariées), en utilisant la fonction \(scipy.stats.chi2.cdf\) du module \(scipy\). Conclure.
#TODO
Le test conduit au rejet de l’hypothèse nulle : les variables lignes et colonnes sont donc manifestement fortement liées.
Pour approfondir la nature des relations entre les modalités lignes et colonnes du tableau, on peut calculer l’indice d’attraction / répulsion, défini par $\(\frac{P(Y=y_k, X=x_l)}{P(Y=y_k)P(X=x_l)}\)$
où \(x_l\) et \(y_k\) sont les profils ligne et colonne. En pratique, cet indice est calculé comme le rapport entre les effectifs observés et théoriques : s’il est supérieur à 1, il y a une attraction ; sinon il y a répulsion entre les modalités.
Calculer cet indice, effectuer uin test du \(\chi^2\) et conclure.
#TODO
Représentation simultanée lignes/colonnes#
En utilisant la fonction \(mapping\) (ligne 329 du fichier base.py), projeter sur le premier plan factoriel les individus ligne et colonne. Interpreter.
#TODO
Comme en ACP où il est possible de reconstituer approximativement les données originelles à partir des coordonnées factorielles des individus, on peut approcher le tableau des indices d’attraction-répulsion \(i_{kl}\) à partir des coordonnées factorielles des modalités lignes et colonnes : en reconstruisant à partir des \(P\) premiers facteurs, si \(F_{kp}\) ett \(G_{lp}\) sont les coordonnées factorielles des modalités lignes et colonnes
\(i_{kl} = 1+\displaystyle\sum_{p=1}^P \frac{F_{kp}G_{lp}}{\sqrt{\lambda_p}}\)
Ainsi :
Deux modalités s’attirent (resp. se repoussent) si leurs coordonnées sont de même signe (resp. de signe contraire) sur les axes factoriels.
Le trait est d’autant plus marqué que les valeurs des coordonnées sont élevées (en valeur absolue) c.-à-d. que les points sont situés aux extrémités des facteurs.
Les coordonnées doivent être relativisées par le pouvoir de restitution du facteur (\(\lambda_h\)).
Calculer l’approximation des inices d’attraction-répulsion à parit des données du premier facteur (P=1). Interpréter.
#TODO
Exercice 2 : Analyse des Correspondances Multiples#
Ici on s’intéresse à 6 traits de caractères de 27 races de chien, et on souhaite analyser le tableau par ACM
chiens = pd.read_table("./data/chiens.txt", header=0, index_col=0, delimiter="\t", encoding="utf-8")
print(chiens)
Taille Poids Velocite Intelligence Affection Agressivite
Chien
Beauceron Taille++ Poids+ Veloc++ Intell+ Affec+ Agress+
Basset Taille- Poids- Veloc- Intell- Affec- Agress+
Berger All Taille++ Poids+ Veloc++ Intell++ Affec+ Agress+
Boxer Taille+ Poids+ Veloc+ Intell+ Affec+ Agress+
Bull-Dog Taille- Poids- Veloc- Intell+ Affec+ Agress-
Bull-Mastif Taille++ Poids++ Veloc- Intell++ Affec- Agress+
Caniche Taille- Poids- Veloc+ Intell++ Affec+ Agress-
Chihuahua Taille- Poids- Veloc- Intell- Affec+ Agress-
Cocker Taille+ Poids- Veloc- Intell+ Affec+ Agress+
Colley Taille++ Poids+ Veloc++ Intell+ Affec+ Agress-
Dalmatien Taille+ Poids+ Veloc+ Intell+ Affec+ Agress-
Doberman Taille++ Poids+ Veloc++ Intell++ Affec- Agress+
Dogue-All Taille++ Poids++ Veloc++ Intell- Affec- Agress+
Epag.-Breton Taille+ Poids+ Veloc+ Intell++ Affec+ Agress-
Epag.-Français Taille++ Poids+ Veloc+ Intell+ Affec- Agress-
Fox-Hound Taille++ Poids+ Veloc++ Intell- Affec- Agress+
Fox-Terrier Taille- Poids- Veloc+ Intell+ Affec+ Agress+
Gd-Bleu-Gasc Taille++ Poids+ Veloc+ Intell- Affec- Agress+
Labrador Taille+ Poids+ Veloc+ Intell+ Affec+ Agress-
Levrier Taille++ Poids+ Veloc++ Intell- Affec- Agress-
Mastiff Taille++ Poids++ Veloc- Intell- Affec- Agress+
Pekinois Taille- Poids- Veloc- Intell- Affec+ Agress-
Pointer Taille++ Poids+ Veloc++ Intell++ Affec- Agress-
St-Bernard Taille++ Poids++ Veloc- Intell+ Affec- Agress+
Setter Taille++ Poids+ Veloc++ Intell+ Affec- Agress-
Teckel Taille- Poids- Veloc- Intell+ Affec+ Agress-
Terre-Neuve Taille++ Poids++ Veloc- Intell+ Affec- Agress-
On récupère les variables actives : on s’intéresse à un sous-ensemble de cardinal \(k\) de variables du jeu de données (vous pouvez changer les variables utilisées).
var_chiens = chiens[['Taille','Velocite','Affection']]
print(var_chiens)
Taille Velocite Affection
Chien
Beauceron Taille++ Veloc++ Affec+
Basset Taille- Veloc- Affec-
Berger All Taille++ Veloc++ Affec+
Boxer Taille+ Veloc+ Affec+
Bull-Dog Taille- Veloc- Affec+
Bull-Mastif Taille++ Veloc- Affec-
Caniche Taille- Veloc+ Affec+
Chihuahua Taille- Veloc- Affec+
Cocker Taille+ Veloc- Affec+
Colley Taille++ Veloc++ Affec+
Dalmatien Taille+ Veloc+ Affec+
Doberman Taille++ Veloc++ Affec-
Dogue-All Taille++ Veloc++ Affec-
Epag.-Breton Taille+ Veloc+ Affec+
Epag.-Français Taille++ Veloc+ Affec-
Fox-Hound Taille++ Veloc++ Affec-
Fox-Terrier Taille- Veloc+ Affec+
Gd-Bleu-Gasc Taille++ Veloc+ Affec-
Labrador Taille+ Veloc+ Affec+
Levrier Taille++ Veloc++ Affec-
Mastiff Taille++ Veloc- Affec-
Pekinois Taille- Veloc- Affec+
Pointer Taille++ Veloc++ Affec-
St-Bernard Taille++ Veloc- Affec-
Setter Taille++ Veloc++ Affec-
Teckel Taille- Veloc- Affec+
Terre-Neuve Taille++ Veloc- Affec-
Analyse des individus#
Dans la suite, on travaille sur le tableau disjonctif complet des données (variables transformées en indicatrices 0/1).
#codage en 0/1 des propriétés des chiens : tableau disjonctif complet
X = pd.get_dummies(var_chiens,prefix='',prefix_sep='')
n,p = X.shape
print(X)
Taille+ Taille++ Taille- Veloc+ Veloc++ Veloc- Affec+ \
Chien
Beauceron False True False False True False True
Basset False False True False False True False
Berger All False True False False True False True
Boxer True False False True False False True
Bull-Dog False False True False False True True
Bull-Mastif False True False False False True False
Caniche False False True True False False True
Chihuahua False False True False False True True
Cocker True False False False False True True
Colley False True False False True False True
Dalmatien True False False True False False True
Doberman False True False False True False False
Dogue-All False True False False True False False
Epag.-Breton True False False True False False True
Epag.-Français False True False True False False False
Fox-Hound False True False False True False False
Fox-Terrier False False True True False False True
Gd-Bleu-Gasc False True False True False False False
Labrador True False False True False False True
Levrier False True False False True False False
Mastiff False True False False False True False
Pekinois False False True False False True True
Pointer False True False False True False False
St-Bernard False True False False False True False
Setter False True False False True False False
Teckel False False True False False True True
Terre-Neuve False True False False False True False
Affec-
Chien
Beauceron False
Basset True
Berger All False
Boxer False
Bull-Dog False
Bull-Mastif True
Caniche False
Chihuahua False
Cocker False
Colley False
Dalmatien False
Doberman True
Dogue-All True
Epag.-Breton False
Epag.-Français True
Fox-Hound True
Fox-Terrier False
Gd-Bleu-Gasc True
Labrador False
Levrier True
Mastiff True
Pekinois False
Pointer True
St-Bernard True
Setter True
Teckel False
Terre-Neuve True
===== Votre travail : =====#
Vous avez à disposition un fichier mca.py, permettant de réaliser les calculs relatifs à une analyse des correspondances multiples Faire une analyse en composantes multiples de ces données et plus précisément :
Déterminer l’importance des axes principaux calculés lors de l’ACP (attribut \(eig\_\), descripion ligne 74 de mca.py).
Déterminer les contributions des points lignes à la variance des axes (attribut r\(ow\_contrib\_\), descripion ligne 86 de mca.py)
Déterminer les contributions des points colonnes à la variance de l’axe (attribut \(col\_contrib\_\), descripion ligne 90 de mca.py)
Déterminer la qualité de représentation des des points lignes et colonnes (attributs \(row\_cos2\_\) et \(col\_cos2\_\), descripion lignes 94 et 97 de mca.py)
Tracer la projection des points lignes et colonnes (fonctions \(mapping\), \(mapping\_row\) et \(mapping\_col\) de mca.py) sur les plans princpaux
Commenter l’ensemble de vos analyses
Calculer la distance entre individus : on utilise dans ce cas la distance du Chi2 sur modalités catégorielles (voir chapitre 1 du cours) qui met en valeur les différences entre les modalités rares
#profil individu moyen
ind_moy = np.sum(X.values,axis=0)/(n*p)
distchi2 = np.zeros(shape=(n,n))
#TODO : calcul de la distance
plt.figure(figsize=(10,10))
sns.heatmap(distchi2,vmin=0,vmax=np.max(distchi2),linewidth=0.1,cmap= 'Greens',xticklabels=chiens.index,yticklabels=chiens.index)
<Axes: >
Ainsi, par exemple, le Basset a plus de caractères en commun avec le Caniche qu’avec le Beauceron.
Calculer la distance à l’origine (profil moyen). Interpréter
#profil moyen des variables-modalités
moda_moy = np.ones(X.shape[0])/n
distO = np.zeros(shape=(1,n))
#TODO : calcul de la distance
sns.heatmap(distO,vmin=0,vmax=np.max(distO),linewidth=0.1,cmap= 'Greens',xticklabels=X.index)
<Axes: >
Ainsi par exemple, le Pointer est plus proche du chien moyen que le Cocker.
Analyse des colonnes#
L’analyse des associations entre les modalités revient à travailler sur les profils colonnes. Le tableau de données est normalisé par les sommes en colonne. Le profil moyen est égal au poids des observations
#somme en colonne
somme_col = np.sum(X.values,axis=0)
n,p = X.shape
#On utilise la distance du Chi2 sur modalités catégorielles qui met en valeur les différences entre les modalités rares
dist = np.zeros(shape=(p,p))
for i in range(p-1):
for j in range(i,p):
dist[i,j] = dist[j,i] = np.sum(n*((X.values[:,i]/somme_col[i]-X.values[:,j]/somme_col[j])**2))
plt.figure(figsize=(10,10))
sns.heatmap(dist,vmin=0,vmax=np.max(dist),linewidth=0.1,cmap= 'Greens',xticklabels=X.columns,yticklabels=chiens.columns)
<Axes: >
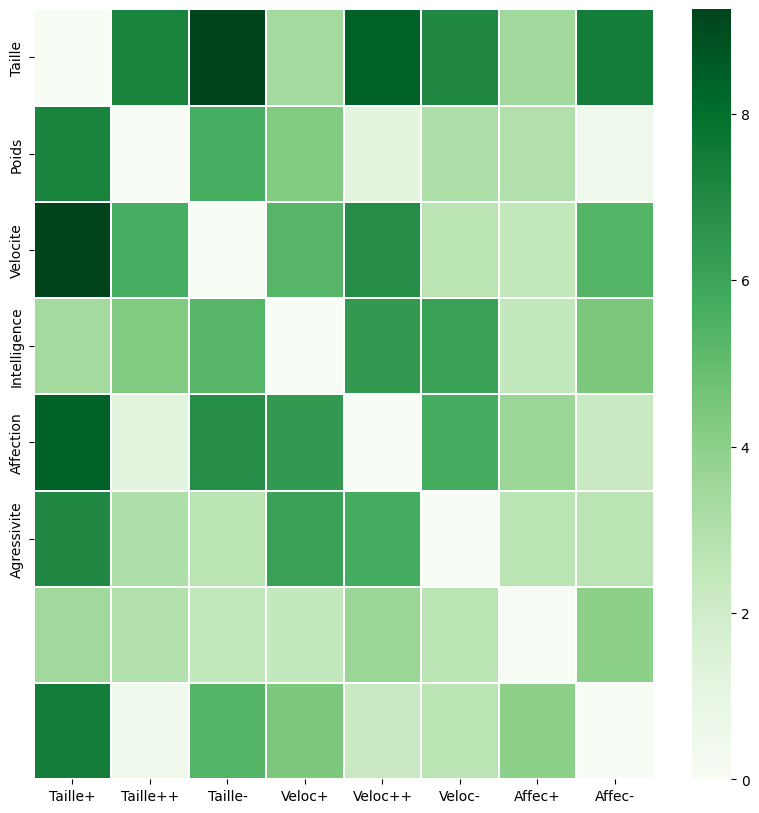
Calculer la distance à l’origine, qui donne une information sur la fréquence de la modalité dans la base. Elle est définie par la disance du \(\chi^2\) au profil moyen. Interpréter
#profil moyen des variables-modalités
moda_moy = np.ones(X.shape[0])/n
distO = np.zeros(shape=(1,p))
#TODO calcul distance
sns.heatmap(distO,vmin=0,vmax=np.max(distO),linewidth=0.1,cmap= 'Greens',xticklabels=X.columns)
<Axes: >
Ainsi, Veloc+ est moins présent que Veloc- dans les exemples.
ACM#
On créé une instance de l’objet MCA (défini dans mca.py) et on estime le modèle des correspondances multiples sur les données \(X\)
from mca import MCA
acm = MCA(row_labels=var_chiens.index, var_labels=var_chiens.columns)
acm.fit(var_chiens.values)
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[24], line 1
----> 1 from mca import MCA
2 acm = MCA(row_labels=var_chiens.index, var_labels=var_chiens.columns)
3 acm.fit(var_chiens.values)
ModuleNotFoundError: No module named 'mca'
Analyse des valeurs propres#
L’objectif de l’Analyse des Correspondances Multiples est de décomposer l’information sur une succession d’axes factoriels orthogonaux. Le nouveau système de représentation est calculé pour préserver au mieux les distances entre individus. L nombre maximum de facteurs est \(p-k\), où \(p\) est la somme du nombre de modalités des variables (le nombre de colonnes de \(X\)), et \(k\) le nombre de variables initiales.
De même que pour l’analyse facrtorielle, calculer les valeurs propres et interpréter les facteurs.
#TODO
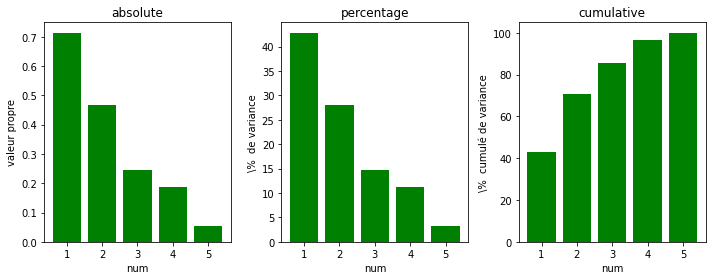
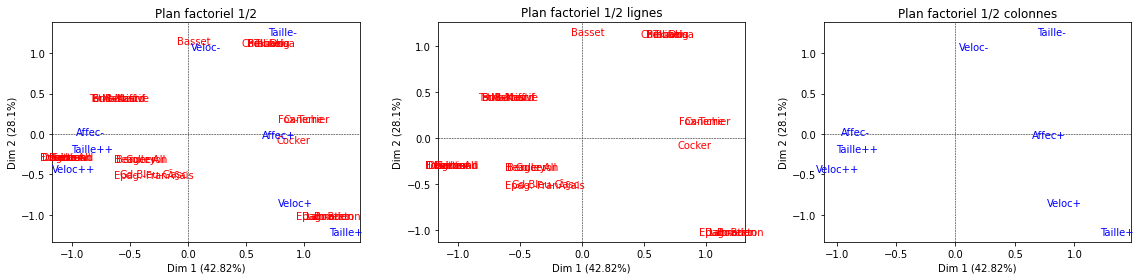
Représentation graphique#
2 types de graphiques peuvent être réalisés :
Les mappings classiques qui représentent les points lignes et colonnes sur un plan factoriel
Des graphiques qui permettent d’interpréter rapidement les axes : on choisit un axe factoriel et on observe quels sont les points lignes et colonnes qui présentent les plus fortes contributions et cos2 pour cet axe
f, (ax1, ax2,ax3) = plt.subplots(1, 3,figsize=(16,4))
acm.mapping(ax1,num_x_axis=1, num_y_axis=2)
acm.mapping_row(ax2,num_x_axis=1, num_y_axis=2)
acm.mapping_col(ax3,num_x_axis=1, num_y_axis=2)
f.subplots_adjust(wspace=0.52)
plt.tight_layout()
f, (ax1, ax2,ax3) = plt.subplots(1, 3,figsize=(16,4))
acm.mapping(ax1,num_x_axis=1, num_y_axis=3)
acm.mapping_row(ax2,num_x_axis=1, num_y_axis=3)
acm.mapping_col(ax3,num_x_axis=1, num_y_axis=3)
f.subplots_adjust(wspace=0.52)
plt.tight_layout()
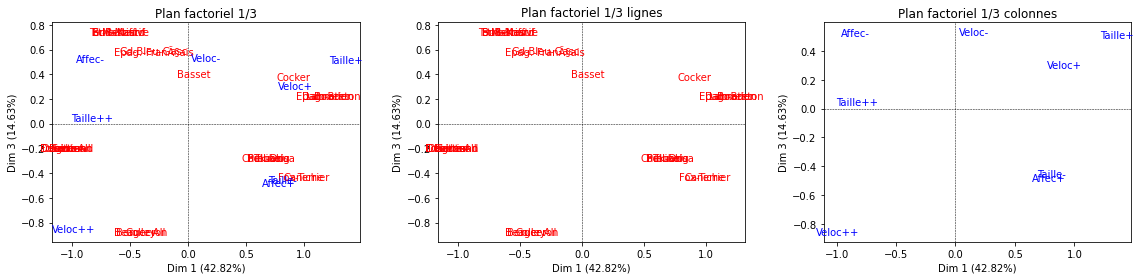
Analyse du 1er axe#
On utilise les formules de \(cos^2\) pour mesurer la qualité de la projection des individus et des modalités sur les axes factoriels. En pratique, si deux individus sont bien projetés alors s’ils sont proches en projections, ils sont effectivement proches dans leur espace d’origine et on peut alors interprèter leur proximité :
— La proximité entre deux individus s’interprète en terme de distance (du \(\chi^2\)) : deux individus se ressemblent s’ils ont choisis les mêmes modalités.
— La proximité entre deux modalités de deux variables différentes s’interprète en terme de distance (du \(\chi^2\)) : deux modalités se ressemblent si elles sont possédées par les mêmes individus.
On peut exhiber les coordonnées des individus sur les facteurs. Par exemple sur le premier facteur
print(pd.DataFrame(acm.row_coord_[:,0],index=var_chiens.index))
0
Chien
Beauceron -0.410650
Basset 0.049305
Berger All -0.410650
Boxer 1.207263
Bull-Dog 0.689967
Bull-Mastif -0.598234
Caniche 0.991235
Chihuahua 0.689967
Cocker 0.905995
Colley -0.410650
Dalmatien 1.207263
Doberman -1.051312
Dogue-All -1.051312
Epag.-Breton 1.207263
Epag.-Français -0.296967
Fox-Hound -1.051312
Fox-Terrier 0.991235
Gd-Bleu-Gasc -0.296967
Labrador 1.207263
Levrier -1.051312
Mastiff -0.598234
Pekinois 0.689967
Pointer -1.051312
St-Bernard -0.598234
Setter -1.051312
Teckel 0.689967
Terre-Neuve -0.598234
et de même pour les modalités
print(pd.DataFrame(acm.col_coord_[:,0],index=X.columns))
0
Taille+ 1.357789
Taille++ -0.830741
Taille- 0.810311
Veloc+ 0.920019
Veloc++ -0.991708
Veloc- 0.156521
Affec+ 0.781744
Affec- -0.841878
\begin{tabular}{lrrr}
\toprule
{} & 0 & 1 & 2 \\
\midrule
Taille+ & 1.357789 & -1.208698 & 0.511177 \\
Taille++ & -0.830741 & -0.183303 & 0.043597 \\
Taille- & 0.810311 & 1.256148 & -0.458548 \\
Veloc+ & 0.920019 & -0.854578 & 0.301665 \\
Veloc++ & -0.991708 & -0.433463 & -0.855715 \\
Veloc- & 0.156521 & 1.073779 & 0.528811 \\
Affec+ & 0.781744 & -0.020376 & -0.484442 \\
Affec- & -0.841878 & 0.021943 & 0.521706 \\
\bottomrule
\end{tabular}
Calculer la moyenne des coordonnées pour chaque variable. Qu’observez-vous ?
#TODO
3.469446951953614e-18
-3.1803263726241462e-18
-6.938893903907228e-18
En utillisant les fonctions plot_row_contrib et plot_row_cos2 (voir fichier base.py), interpréter la contribution des individus aux deux premiers facteurs.
#TODO
Analyse du deuxième axe#
#TODO
