TP Statistiques descriptives#
import numpy as np
import matplotlib.pyplot as plt
Le notebook et les données sont téléchargeables ici
Statistique monovariée#
Le tableau suivant donne les notes (sur 10) obtenues à un examen par un groupe d’élèves. \(\begin{array}{c|c} Nom & Note \\ \hline Alain &6\\ Raymond &5\\ Jean-Joseph &9\\ Eglantine &3\\ Isidore &3\\ Mauricette &1\\ Sylvère &9\\ Pétunia &6\\ Philemon &5\\ Archibald &6\\ Théodule &5\\ Marguerite &6\\ Proserpine &5\\ Alphonse &7\\ Géraud &5\\ Basile &10\\ Fantine &2\\ Sidonie &1\\ Thérèse &1\\ Yves &1 \end{array}\)
notes = np.array([6, 5, 9, 3, 3, 1, 9, 6, 5, 6, 5, 6, 5, 7, 5, 10, 2, 1, 1, 1])
Donner les différentes modalités possibles
#TODO
Calculer les effectifs cumulés de chaque modalité.
#TODO
Calculer les effectifs par modalité, les fréquences et les fréquences cumulées des notes
#TODO
Représenter avec un (ou plusieurs) graphique(s) adapté(s) la répartition des notes
#TODO
En déduire (et afficher) la fonction de répartition empirique des notes.
#TODO
En utilisant la fonction boxplot, tracer la boîte à moustache des notes.
#TODO
Calculer les éléments caractéristiques (indicateurs de tendance, de dispersion) des notes.
#TODO
Statistique bivariée#
Cas de variables quantitatives#
On donne le fichier de données suivant
X=np.loadtxt('./data/bivariee.txt',delimiter=',')
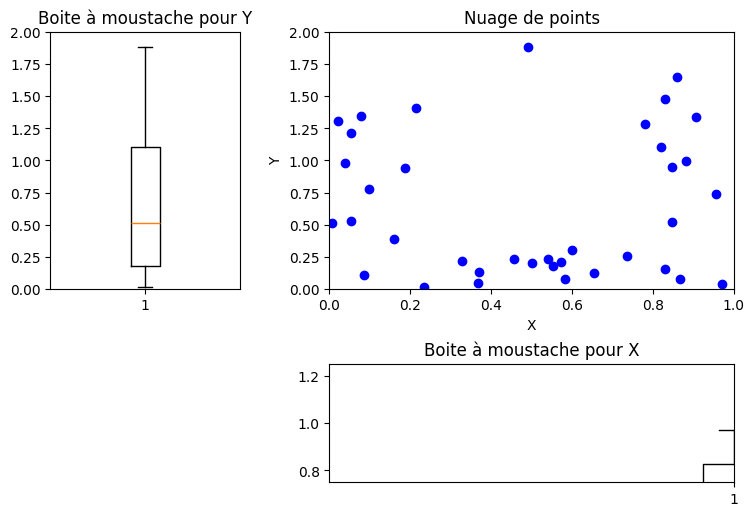
plt.figure(figsize=(12,8))
plt.subplot(2,2,2)
plt.plot(X[:,0],X[:,1],'ob')
plt.axis([0,1,0,2])
plt.title('Nuage de points')
plt.xlabel('X')
plt.ylabel('Y')
plt.subplot(4,2,6)
plt.subplots_adjust(hspace=0.4, wspace=0.3)
plt.boxplot(X[:,0],0,'+',0)
plt.axis([0,1,0.75,1.25])
plt.title('Boite à moustache pour X')
plt.subplot(2,4,2)
plt.boxplot(X[:,1],0,'+',1)
a = plt.axis()
plt.axis([a[0], a[1], 0, 2])
plt.title('Boite à moustache pour Y')
plt.show()
/var/folders/k2/63jxpq5j3b78v_1h6tdfk88m0000gp/T/ipykernel_6836/3659791477.py:13: MatplotlibDeprecationWarning: Passing the notch parameter of boxplot() positionally is deprecated since Matplotlib 3.9; the parameter will become keyword-only in 3.11.
plt.boxplot(X[:,0],0,'+',0)
/var/folders/k2/63jxpq5j3b78v_1h6tdfk88m0000gp/T/ipykernel_6836/3659791477.py:18: MatplotlibDeprecationWarning: Passing the notch parameter of boxplot() positionally is deprecated since Matplotlib 3.9; the parameter will become keyword-only in 3.11.
plt.boxplot(X[:,1],0,'+',1)
Calculer la covariance entre les deux variables. Conclusion ?
#TODO
Calculer la corrélation entre les deux variables. Conclusion ?
#TODO
Cas de variables qualitatives#
On s’intéresse à un fichier décrivant la réussite d’étudiants en mathématiques (données décrites ici)
import pandas as pd
result = pd.read_csv('./data/student.csv',delimiter=';')
print(result)
school sex age address famsize Pstatus Medu Fedu Mjob Fjob \
0 GP F 18 U GT3 A 4 4 at_home teacher
1 GP F 17 U GT3 T 1 1 at_home other
2 GP F 15 U LE3 T 1 1 at_home other
3 GP F 15 U GT3 T 4 2 health services
4 GP F 16 U GT3 T 3 3 other other
.. ... .. ... ... ... ... ... ... ... ...
390 MS M 20 U LE3 A 2 2 services services
391 MS M 17 U LE3 T 3 1 services services
392 MS M 21 R GT3 T 1 1 other other
393 MS M 18 R LE3 T 3 2 services other
394 MS M 19 U LE3 T 1 1 other at_home
... famrel freetime goout Dalc Walc health absences G1 G2 G3
0 ... 4 3 4 1 1 3 6 5 6 6
1 ... 5 3 3 1 1 3 4 5 5 6
2 ... 4 3 2 2 3 3 10 7 8 10
3 ... 3 2 2 1 1 5 2 15 14 15
4 ... 4 3 2 1 2 5 4 6 10 10
.. ... ... ... ... ... ... ... ... .. .. ..
390 ... 5 5 4 4 5 4 11 9 9 9
391 ... 2 4 5 3 4 2 3 14 16 16
392 ... 5 5 3 3 3 3 3 10 8 7
393 ... 4 4 1 3 4 5 0 11 12 10
394 ... 3 2 3 3 3 5 5 8 9 9
[395 rows x 33 columns]
On regarde les deux premières colonnes des données (code de l’école et genre de l’étudiant)
x = result.values[:,0]
g = result.values[:,1]
Construire le tableau de contingence de ces deux variables
#TODO
Construire le tableau théorique associé en supposant l’indépendance des deux variables.
#TODO
Calculer la distance du \(\chi^2\) entre les variables \(x\) et \(g\). Ces deux variables sont elles liées ou sont elles indépendantes ?
#TODO
On s’intéresse maintenant à la septième variable \(ne\) qui code le niveau d’éducation des mères de la manière suivante :
0 - none,
1 - primary education (4th grade),
2 - 5th to 9th grade,
3 - secondary education
4 - higher education
Récupérer cette variable et calculer les effectifs de chacune des modalités. Calculer le tableau de contingence entre les variables \(x\) et \(ne\)
#TODO
#TODO
Les effectifs étant trop faibles, fusionner les deux premières colonnes
#TODO
Construire le tableau théorique, en supposant l’indépendance des variables
#TODO
Calculer la distance du \(\chi^2\) entre les variables \(x\) et \(ne\). Ces deux variables sont elles liées ou sont elles indépendantes ? Que peut on en déduire sur le choix de l’école ?
#TODO
